Алгоритмы обслуживания очередей

 

Чаще всего применяю следующие алгоритмы управления (обслуживания) очередями:

• FIFO

• Приоритетное обслуживание, которое называют также «подавляющим»

• Взвешенное обслуживание

• 1) Традиционный алгоритм FIFO

Достоинство — простота реализации и отсутствие необходимости конфигурирования. Недостаток — невозможность дифференцированной обработки заявок различных потоков.

• 2) Приоритетное обслуживание (Priority Queuing)

Сначала необходимо решить отдельную задачу - разбить общий входной поток устройства на классы (приоритеты). Признак, по которому производят разбивку на классы, помещают в поле приоритета.

Затем требование помещается в очередь, соответствующую заданному приоритетному классу.

Рассмотрим пример с четырьмя приоритетными очередями: высокий, средний, нормальный и низкий приоритет.

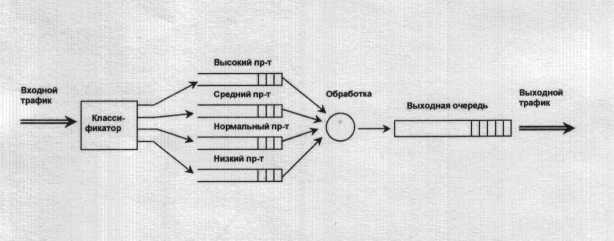
Рис. 5.12. Приоритетное обслуживание

Здесь очереди имеют абсолютный приоритет — пока не обработаны пакеты из очереди более высокого приоритета не производится переход к более низкоприоритетной очереди.

При моделировании можно:

■ Выделить одинаковое количество буферов для всех очередей

• На основе анализа трафика поступлений установить нужный размер для каждой из очередей.

Недостаток:

Если высока интенсивность высокоприоритетного трафика, обслуживание низкоприоритетного трафика может совсем не производиться.

Этот метод можно, например, использовать при моделировании сети, если в качестве высокоприоритетного будет выбран голосовой трафик (IP-телефония). Это связано с тем, что его интенсивность невелика (обычно 4-16 Кбит/с).

Если же в сети в качестве высокоприоритетного выбран видеотрафик, остальным потокам может и не достаться пропускной способности.

Взвешенные настраиваемые очереди (Weighted Queuing)

Здесь делается попытка предоставить всем классам определенный минимум пропускной способности, т.е. обслуживания, и гарантировать некоторые требования к задержкам.

Под весом для каждого класса понимается процент предоставляемой классу пропускной способности (от полной выходной пропускной способности). Алгоритм, используемый администратором для назначения весов, называется настраиваемой очередью.

 

 

 

Рис.5.13. Взвешенные настраиваемые очереди

Очереди обслуживаются циклически, и в каждом цикле обслуживания из каждой очереди выбирается такой объем нагрузки, который соответствует весу этой очереди.

Например: цикл = 1 сек., скорость выходного интерфейса = 100 Мбит/с. В каждом цикле из очередей выбираются следующие объемы данных:

■ 1 — 10 Мбит

■ 2—10 Мбит

■ 3 — 30 Мбит

■ 4 — 20 Мбит

■ 5 — 30 Мбит

Здесь, как и в приоритетном обслуживании, можно назначать различные длины очередям. Тем самым появляется возможность сглаживания нагрузки.

 

Вопросы и задания

1. Измените алгоритм моделирования СМО так, чтобы он учитывал возможность существования неограниченной очереди к приборам (потерянных заявок не будет). При этом используйте семафор.

2. Сравните по быстродействию три способа организации календаря: простой список, связный список, двусвязный список.

 

Оценки искомых характеристик и их дисперсии

Структура оценок

Следуя традициям математической статистики, обозначим искомую характеристику символом q, а ее приближенную оценку, найденную в результате моделирования . При моделировании СМО, как правило, оценки имеют вид дроби - отношения двух статистик

Это обусловлено тем, что нахождение оценки при имитационном моделировании обычно связано с осреднением, В числителе стоит некоторая сумма, накопленная в процессе имитации, а в знаменателе величина, характеризующая число слагаемых в этой сумме. Приведем несколько примеров.

1. q - вероятность потери заявки

а. Оценка по заявкам. Здесь h - число поступивших заявок, x - число потерянных.

б. Оценка по времени. Здесь h - пройденное системное время (длина реализации), x - суммарное время, в течение которого система была полностью занята (пришедшую в это время заявку некуда принять и поэтому она теряется).

В оценке 16 знаменатель не характеризует количество слагаемых в явном виде. Однако аналогию нетрудно усмотреть. Предположим, что время отсчитывается дискретно, и Dt - единица -времени. Тогда h - количество интервалов Dt, пройденных в процессе имитации, а x - количество интервалов, на которых наблюдалась полная занятость. В этом случае каждое из слагаемых числителя равно либо единице (если система полностью занята), либо нулю (в иных случаях), а знаменатель представляет собой количество слагаемых. Предположение о дискретном счете времени является даже не предположением, а фактом ввиду ограниченной разрядности ЭВМ. Под Dt можно понимать цену младшего разряда в представлении величин, связанных с системным временем.

 

2. q - среднее время ожидания начала обслуживания

а. Оценка по заявкам с раздельным учетом времени ожидания. h - число обслуженных заявок, x - суммарное время, проведенное этими заявками в очереди (в буфере). Для каждой заявки надо хранить момент ее прихода t' и момент поступления на обслуживание t''.

Величина  складывается из разностей .. Для тех заявок, которые сразу попадают на обслуживание, эта разность равна нулю. Хранить t^/ и t^// надо только до тех пор, пока их разность не добавлена в статистику , после этого их можно стереть из памяти. Добавление производится на том шаге, на котором имитируется поступление заявки на обслуживание.

б. Совместный учёт времени ожидания. Можно обойтись без запоминания моментов t^/ и t^// если вычислять  по шагам. На каждом шаге к накопленному значению  добавляется произведение (t_T-t_L) l, в котором (t_T-t_L)- системное время, пройденное от момента предыдущего события до момента текущего события, l - количество заявок, стоявших в очереди на этом интервале.

 

3. q-средняя длина очереди

Необходимо уточнить смысл слова «средняя». Если интересоваться длиной очереди в произвольный момент времени, надо усреднять по всему пройденному времени. Если же интересоваться длиной очереди в момент прихода заявки, то надо рассматривать только моменты прихода заявок. Эти средние длины очереди, вообще говоря, неодинаковы. Приведём простой пример. Допустим, заявка некоторое время ждёт начала обслуживания, но успевает поступить на обслуживание к моменту появления следующей заявки, и так происходит для всех заявок. Тогда в момент прихода заявки длина очереди всегда равна нулю, и средняя длина очереди, следовательно, тоже равна нулю. Но средняя длина очереди по отношению к произвольному моменту времени не равна нулю, так как на некоторых отрезках времени длина очереди равна единице.

 

3. ^/ Средняя длина очереди в момент поступления заявки.

- число поступивших заявок; 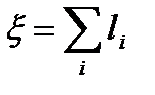, где l _i - длина очереди в момент поступления i -й заявки.

3.^// Средняя длина очереди в произвольный момент времени

-пройденное системное время (длина реализации); - то же, что в примере 2б, только роли другие: там (t_T-t_L) – усредняемая величина, а l - коэффициент; здесь же l -усредняемая величина, а (t_T-t_L) - коэффициент.

Поясним, почему в третьем примере варианты помечены штрихами, а не буквами, как в первых двух примерах. Это сделано, чтобы подчеркнуть различие: в третьем примере рассматриваются разные характеристики СМО, а в первых двух - разные виды оценок.

На этих трёх примерах мы убедились, что оценки имеют вид дроби. Рассмотрим теперь, как формируются числитель и знаменатель. Это - статистики, накапливаемые по шагам в ходе имитации. В состав алгоритма шага входят операторы, добавляющие к статистикам  и  приращения. Выбор той или иной оценки в конечном итоге сводится к определению вида этих приращений. Рассмотрим вид приращений для приведённых выше примеров оценки.

 

 

1а. Вероятность потери заявки, оценка по заявкам

ì1, если на данном шаге поступила и потеряна заявка,

Dx=í

î0 в иных случаях

 

 

ì1, если на данном шаге поступила заявка,

Dh=í

î0 в ином случае.

 

1б. Вероятность потери заявки, оценка по времени

ì(t_T-t_L), если перед началом шага система полностью занята,

Dx=í

î0 в ином случае

 

Dh = t_T-t_L (на всех шагах, независимо от их типа).

t_Т – момент текущего события (текущее системное время),

t_L – момент предыдущего события.

 

2а. Среднее время ожидания, раздельный учёт ожидания

ì t^// - t^/, если на данном шаге завершилось обслуживание заявки (т.е. освободился прибор)

Dx=í

î0 в иных случаях

 

t^/, t^// - соответственно момент прихода этой заявки и момент начала обслуживания (они могут совпадать, тогда будет Dx=0).

ì1, если на данном шаге освободился прибор

Dh=í

î0 в ином случае.

 

2б. Среднее время ожидания, совместный учёт

Dh = (t_T-t_L) l (на всех шагах, независимо от их типа).

l - длина очереди перед началом шага (число занятых ячеек буфера; может быть равно и нулю)

ì1, если на данном шаге освободился прибор

Dh=í

î0 в ином случае.

 

 

3^/. Средняя длина очереди в момент прихода заявки

ì l, если на данном шаге поступила и потеряна заявка,

Dx=í

î0 в иных случаях

 

ì1, если на данном шаге поступила заявка,

Dh=í

î0 в ином случае.

 

3^//. Средняя длина очереди в произвольный момент времени

Dx = (t_T-t_L) l

Dh = t_T-t_L

 

По аналогии с приведёнными примерами можно выбрать вид оценки и приращений для других случаев с учётом смысла оцениваемой характеристики. Оценки некоторых характеристик можно вычислить через оценки других характеристик. Например, оценку коэффициента загрузки буфера можно вычислить по формуле

Вопросы и задания:

1. Термин «статистика» употребляется во многих смыслах:

а) математическая наука, изучающая методы оценки параметров и проверки гипотез о законах распределения по результатам наблюдений (математическая статистика);

б) совокупность данных о явлениях, имеющих случайный характер (в этом смысле говорят «сбор статистики»)

в) функция выборки, т.е. функция, аргументами которой являются наблюдавшиеся значения случайной величины.

В каком смысле мы говорим, что оценка характеристики СМО обычно является отношением двух статистик?

2. Термин «оценка» тоже имеет несколько смыслов:

а) приближённое значение неизвестного параметра, вычисленное по выборке (точнее было сказать «значение оценки»);

б) правило (алгоритм или формула), по которому вычисляется значение оценки по выборке (в этом смысле можно говорить о свойствах оценки: несмещённости, состоятельности, эффективности, достаточности);

в) процесс выбора правила и вычисления по нему значения оценки (такой смысл имеет заголовок главы «оценка параметров» в учебниках по математической статистике, хотя в некоторых книгах пишут более удачно: «оценивание параметров»). В каком смысле употребляется термин «оценка» в этом разделе? В каком смысле можно утверждать, что оценка является статистикой?

3. Постройте оценки для следующих характеристик:

а) средняя длина очереди в момент освобождения прибора;

б) вероятность того, что в произвольный момент времени все приборы свободны;

в) среднее время пребывания обслуженной заявки в системе (время ожидания в очереди плюс время обслуживания).

Иными словами, укажите, что представляют собой x, h, Dx, Dh?

4. Подумайте, всегда ли оценки 1а и 1б совпадают в среднем с вероятностью потери заявки. Если не всегда, то какая из двух оценок непригодна и чем это объяснить? (Ответ есть в следующем разделе).

 

6.2. Дисперсия оценки (точность результатов моделирования)

При моделировании методом Монте-Карло многократно повторяются опыты со случайным исходом и оценка искомого результата определяется путем осреднения результатов отдельных опытов:

 

(6.1)

 

где x_i результат i -го опыта.

Алгоритм моделирования строится так, что математическое ожидание результата одного опыта совпадает с искомым результатом, т.е.

 

(6.2)

 

При этом оценка (6.2) оказывается несмещенной, т.е.

 

(6.3)

 

Хотя в среднем оценка совпадает с q, вкаждом конкретном случае она отличается от qна случайную величину, средний квадрат которой представляет собой дисперсию оценки. Чем больше дисперсия, тем больше случайные отклонения оценки от искомого ре­зультата, то есть меньше ее точность. С увеличением числа опытов дис­персия оценки уменьшается, а точность, соответственно, растет. Ниже выводятся правило, указывающее до какой величины надо снижать дисперсию путем увеличения числа опытов, чтобы можно было считать оценку достаточно точной.

Поскольку оценка является случайной величиной, точность ее рассматривается применительно ко всему множеству возможных значе­ний оценки с учетом вероятностей этих значений. Требования к точ­ности обычно формулируются в виде вероятностного утверждения:

 

(6.4)

 

где D_доп – допустимая погрешность;

γ – заданный коэффициент до­верия.

В конкретном случае значение оценки может отличаться от искомого результата больше чем на D_доп. Однако с вероятностью γ это
не произойдет, если условие (6.4) соблюдено.

Связь между D_доп и γ зависит от распределения оценки Согласно центральной предельной теореме теория вероятностей, оцен­ка (6.1) имеет распределение, близкое к нормальному, если n не слишком мало. С учетом (6.3) можно записать

 

 

Следовательно,

 

Это соотношение позволяет, задав D_доп = σ, вычислить

 

 

где Ф (.) – интегральная функция стандартного нормального распределения

N (0, 1). В частности, для k = 1,2,3 значение γравно соответственно 0.6826; 0.9545; 0.9973. Утверждая, что погрешность не превышает 3σ, мы ошибаемся менее чем в трех случаях из 1000. Следовательно, обеспечив σ = γ/3, можно быть достаточно уверенным, что погрешность не превысит допустимого значения.

Из сказанного вытекает практическая рекомендация: число опытов при моделировании должно быть настолько большим, чтобы дисперсия оценки снизилась до величины

(6.5)

 

где выбор k определяется требуемым коэффициентом доверия. Чтобы применять это правило остановки, необходимо уметь вычислять дисперсию оценки при заданном числе опытов γ.

Оценка по множеству независимых реализаций. Для многих случаев результаты опытов представляют собой повторную выборку (x ₁+..+ x_n), то есть совокупность независимых реализаций с.в. Х. Математическое ожидание ее должно совпадать с θ. Дисперсию этой с.в. обозначим Поскольку реализации независимы, дисперсия оценки (6.1) равна

В соответствии о правилом (6.5) требуемое число опытов равно

 

(6.6)

 

Таким образом, требуемое число опытов обратно пропорционально квадрату допустимой погрешности. Этим обусловлена трудность получения высокой точности результатов при вероятностном моделировании.

Особые трудности возникают, когда искомым результатом является вероятность некоторого события, причем вероятность малая. В этом случае

 

 

 

Требуемое число опытов удобно выразить через допустимую отно­сительную погрешность

 

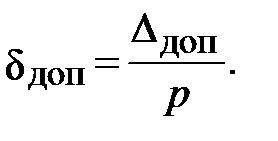
Формула (6.6) принимает вид

 

(6.7)

 

Чем меньше вероятность р, тем больше требуется опытов для обеспечения допустимой относительной погрешности. При малых вероятностях даже грубая оценка требует слишком много опытов. Например, при р порядка 10^-5, k = 3, d_доп = 0,3 формула (6.7) дает n =10⁷. Обычно такое число опытов требует много машинного вре­мени.

Заметим, что в формулу (6.6) входит величина , которая заранее не известна. Ее приближенно находят в процессе моделирования по формуле

 

 

Проделав некоторое число опытов, вычисляют , а затем по формуле (6.6) находят примерно необходимое число опытов. Опыты продолжают до получения нужного их числа, после чего можно заново вычислить уже более точно. Аналогично поступают с величиной р. Вначале пробным моделированием определяют

 

 

а затем подставляют найденное значение в формулу (6.7). По мере увеличения количества опытов значения можно эпизодически уточнять.

Рассмотрим способы определения ₁ по выборке.

1. оценка по двум статистикам:

Эти статистики формируются в двух ячейках. По окончании очередного прогона в первую добавляется вычисленная оценка, а во вторую - её квадрат. Когда проведено n прогонов, вычисляется оценка дисперсии:

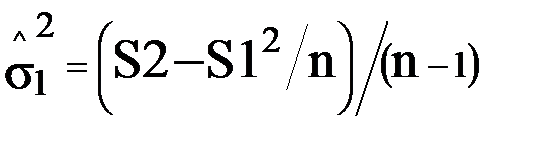
2. оценка по размаху:

где W- коэффициент между максимальными и минимальными элементами выборки. Коэффициент , на который надо разделить размах W, зависит от числа элементов выборки. Если элементы выборки распределены по нормальному закону (а для это верно), то можно найти в таблицах математической статистики. В частности, (10)=3.08, (20)=3.73.

Известен способ нахождения дисперсии оценки по одной реализации, разделённой точками регенерации на независимые отрезки. Точкой регенерации называется такой момент времени, после которого процесс развивается независимо от того, как он развивался этого момента. В точке регенерации процесс как бы начинается заново. При моделировании СМО точкой регенерации является момент, когда в пустую систему поступает заявка. Так как система пустая, её прошлые состояния не оказывают влияния на будущие состояния. Для приближённого вычисления дисперсии надо иметь хотя бы несколько десятков точек регенерации, т.е. за один прогон система должна несколько десятков раз опустеть. Если ввести исходные данные, соответствующим реальным СМО, то придётся очень долго ждать возвращения системы в полностью свободное состояние, так как реальные СМО работают с достаточной нагрузкой и пустыми практически не бывают. Однако за точку регенерации не обязательно брать пустую систему. Можно брать то состояние системы, к которому она чаще всего возвращается. При нагрузке r³0.5 таким состоянием может быть состояние, когда в системе находиться одна, две или даже более заявок.

 

Вопросы и задания:

1. Какая оценка называется несмещённой?

2. Почему вместо погрешности оценки можно интересоваться дисперсией оценки либо среднеквадратическим отклонением?

3. Во сколько раз надо увеличить длину реализации, чтобы уменьшить дисперсию оценки в десять раз?

4. Во сколько раз надо увеличить длину реализации, чтобы уменьшить погрешность оценки в десять раз?

5. Сколько примерно шагов надо выполнить, чтобы оценить вероятность события, примерно равную 10^-4 с точностью порядка 20%?

6. Сопоставьте два варианта, одинаковых по затратам машинного времени: а)десять прогонов с длиной реализации Т; б) один прогон с длиной реализации 10Т. В чём преимущество первого варианта?

 

⇐ Предыдущая9101112131415161718Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: