Уравнение затухающих колебаний

КОМИТЕТ РОССИЙСКОЙ ФЕДЕРАЦИИ

ПО РЫБОЛОВСТВУ

АСТРАХАНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

 

кафедра физики

 

Методические рекомендации для выполнения лабораторной работы

по физике:

«ОПРЕДЕЛЕНИЕ ЖЕСТКОСТИ ПРУЖИНЫ И ПАРАМЕТРОВ ЗАТУХАНИЯ КОЛЕБАНИЙ НА ПРУЖИННОМ МАЯТНИКЕ».

 

Для студентов всех специальностей

очной и заочной формы обучения.

 

 

астрахань – 2010 г.

Лабораторная работа

 

ОПРЕДЕЛЕНИЕ ЖЕСТКОСТИ ПРУЖИНЫ И ПАРАМЕТРОВ ЗАТУХАНИЯ КОЛЕБАНИЙ НА ПРУЖИННОМ МАЯТНИКЕ

 

Цель работы: определение жесткости пружины статическим и динамическим методами, изучение затухающих колебаний на примере упругих колебаний пружинного маятника.

Оборудование: лабораторный стенд, закрепленный на нем горизонтальный стержень с отверстием для крепления пружины, секундомер, пружина, набор грузов, метровая линейка.

Теоретическое введение

Деформации

Все реальные тела деформируемы. Под действием приложенных сил они меняют свою форму или объем. Такие изменения называются деформациями. В случае твердых тел различают два предельных случая: деформации упругие и деформации пластические. Упругими называют деформации, исчезающие после прекращения действия приложенных сил. Пластическими или остаточными деформациями называют такие деформации, которые сохраняются в теле, по крайней мере частично, и после прекращения действия внешних приложенных сил. На пластических деформациях основана холодная обработка металлов — штамповка, ковка и пр. Является ли деформация упругой или пластической зависит не только от материала тела, но и от приложенных сил. Если сила (точнее, сила, отнесенная к единице площади, т. е. напряжение) не превосходит известной величины, называемой пределом упругости, то возникающая деформация будет упругой. Если же она превосходит этот предел, то возникающая деформация будет пластической. Предел упругости имеет различные значения для разных материалов. Он является не вполне четко определенной величиной. Разделение тел на упругие и пластические также в какой-то степени условно. Строго говоря, все деформации после прекращения действия внешних сил исчезают не полностью, а поэтому являются пластическими. Однако если остаточные деформации малы, то во многих случаях их можно не принимать во внимание. Как велика должна быть остаточная деформация, чтобы можно было так поступать, зависит от конкретных условий. В некоторых случаях, например, можно пренебречь остаточными деформациями, если они не превосходят 0,1% от максимальных значений, достигавшихся под действием приложенных сил. В других случаях этот предел должен быть снижен до 0,01 % и т. д.

В настоящей работе мы ограничимся изучением только упругих деформаций. При этом мы остановимся только на механике, но не на физике явлений. Механика описывает упругие свойства тел посредством некоторых эмпирически вводимых упругих постоянных, различных для различных тел и зависящих от их физического состояния (например, от температуры). Более глубоким является физический подход, рассматривающий явление деформаций с атомистической точки зрения. Этим занимается теория твердого тела. Она позволяет в принципе не только вывести основные уравнения механики деформируемых тел с атомистической точки зрения, но и установить связь между упругими постоянными вещества и другими его физическими свойствами.

Тела мы будем считать идеально упругими. Так называются идеализированные тела, которые могут претерпевать только упругие, но не пластические деформации. Такими идеализациями можно пользоваться, когда силы, приложенные к реальным телам, не превосходят предела упругости. Для идеально упругих тел существует однозначная зависимость между действующими силами и вызываемыми ими деформациями. В случае пластических деформаций такой однозначной связи не существует. Это видно хотя бы из того, что до и после пластической деформации тело имеет различную форму, хотя в обоих случаях оно не подвергается действию внешних сил. Мы ограничимся изучением только малых деформаций. Малыми называются упругие деформации, подчиняющиеся закону Гука. Это приближенный закон, согласно которому деформации пропорциональны силам, их вызывающим.

Рассмотрим тело подвешенное на пружине – пружинный маятник. Если это тело вывести из положения равновесия, то оно будет совершать колебательное движение (колебания).

Колебательным движением называется процесс, при кото­ром система многократно отклоняясь от положения равнове­сия, каждый раз вновь возвращается к нему.

В зависимости от характера воздействия на колеблющуюся систему различают свободные (собственные) и вынужденные колебания.

Свободные колебания

Свободные колебания имеют место, когда на колеблющееся тело действует только возвращающая сила F, которая стремит­ся вернуть тело, отклоненное от положения равновесия в это положение. Свободные колебания являются незатухающими, если не происходит рассеяние энергии в окружающее пространство. В противном случае мы говорим, что на тело кроме возвраща­ющей силы действует сила сопротивления (или сила трения) F _тр. Вынужденные колебания совершаются под действием внешней периодически изменяющейся силы, которая называется вынужда­ющей.

В данной работе изучаются закономерности свободных колеба­ний пружинного маятника. Пружинной маятник представляет собой груз массой m, подвешенный на упругой пружине жесткостью k (рис.1). В случае положения равновесия (груз в покое, x = 0) сила тяжести mg уравновешивается упругой силой растяжения пружины (F=mg). Если отклонить тело от положения равновесия на величину x=A ₀ и отпустить его, то оно будет совершать колебания. При определённых условиях (небольшом смещении, достаточно тяжёлом грузе, при большой жёсткости пружины, за небольшой промежуток времени) колебания можно счи­тать незатухающими, совершаемыми под действием силы упру­гости, которая по закону Гука равна:

F = - k x, (1)

где k – коэффициент жесткости пружины.

По II закону Ньютона:

F = ma, , ,

(2)

Выражение (2) является дифференциальным уравнением свободных незатухающих колебаний. Решение этого уравнения представляет собой зависимость x (t), которая имеет вид:

(3)

где А ₀ – амплитуда – величина наибольшего отклонения от положения равновесия, ее значение определяется величиной начального воздействия, которым система была выведена из положения равновесия; - фаза колебаний; φ₀ – начальная фаза.

График этой зависимости представлен на рис.2.

Подставляя (3) в (2) и учитывая, что:

, при φ ₀=0получаем:

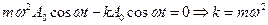или

Выразим период: (4)

Из (4) следует, что для данной пружины квадрат периода коле­баний прямо пропорционален массе тела.

Затухающие колебания

Уравнение затухающих колебаний

В любой реальной колебательной системе есть силы сопро­тивления (трения), действие которых приводит к уменьшению амплитуды и энергии колебаний. Такие свободные колебания называют затухающими.

Будем исходить из основного уравнения динамики, полагая, что на частицу массы т действует кроме квазиупругой силы (-kх)сила сопротивления, пропорциональная скорости части­цы (простейший, и вместе с тем наиболее часто встречающийся случай), ,где r — коэффициент сопротивления (величина размерная). Тогда уравнение движения будет иметь вид

, (5)

или

, (6)

где 2β = r / m, . Отметим, что ω₀ — это частота свобод­ных колебаний без трения. Частоту ω₀ называют собственной частотой осциллятора, а β — коэффициентом затухания.

Эксперимент показывает, что смещение x точки от положения равновесия удовлетворяет зависимости

, (7)

где a ₀ – амплитуда колебаний в начальный момент времени и α – начальная фаза колебаний. Анализ выражения (7) показывает, что величина ωявляется частотой затухающих колебаний. Можно установить зависимость величины ω от параметров ω₀ и β, если, пользуясь выражением (7), найти 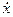, 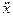и подставить найденные выражения в (6). После преобразований (проведите их самостоятельно) получим:

. (8)

График функции (3.3) показан на рис. 3 для случая х ₀ > 0 и . Затухающий колебательный процесс не является в строгом смысле пери­одическим. Действительно, рассмотрим момент времени t_n, когда cos(ω t_n + α) = 1 и следовательно x (t_n) =a (t_n) = . Ясно, что при любом t > t_n x (t) < x (t_n), т. е. значение функции x (t_n)не повторяется ни при каких t > t_n. Ясно в то же время, что благодаря гармоническому множителю cos(ω t + α)функция x (t)обладает определенной повторяемостью: в частности, повто­ряются через равные промежутки времени как нулевые значения функции x (t), так и ее максимумы и минимумы. Поэтому величину Т = 2π/ω принято называть периодом зату­хающих колебаний:

. (9)

Множитель а = а ₀е^{-β t} перед косинусом в (7) называют ам­плитудой затухающих колебаний (пунктир на рис. 3).

Поделиться:

Воспользуйтесь поиском по сайту: