шар и сфера .Цилиндр и конус

1. Сфера − это геометрическое место точек в пространстве, равноудаленных от некоторой заданной точки (центра сферы). Расстояние между любой точкой сферы и ее центром называется радиусом. Геометрическое тело, ограниченное сферой, называется шаром.

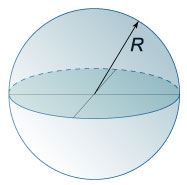
2. Площадь сферы
S=4πR2

3. Объем шара
V=4πR33

4. Шаровым сегментом называется часть шара, отсекаемая плоскостью.

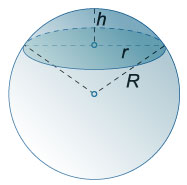
5. Соотношение между высотой и радиусом основания сегмента и радиусом шара
R=r2+h22h,
где h − высота сегмента, r − радиус основания сегмента, R − радиус шара.

6. Площадь основания шарового сегмента
Sосн=πr2

7. Площадь внешней поверхности шарового сегмента
Sсегм=π(h2+r2)

8. Площадь полной поверхности шарового сегмента
S=Sосн+Sсегм=π(h2+2r2)=π(2Rh+r2)

9. Объем шарового сегмента
V=πh2(3R−h)6=πh(3r2+h2)6

10. Шаровым слоем называется часть шара, заключенная между двумя параллельными плоскостями.

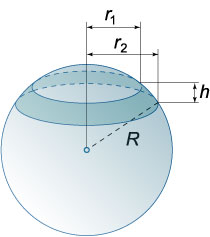
11. Площадь внешней поверхности шарового слоя
Sсл=2πRh,
где h − высота шарового слоя, R − радиус шара.

12. Площадь полной поверхности шарового слоя
S=Sсл+S1+S2=π(2Rh+r21+r22),
где h − высота шарового слоя, R − радиус шара, r1, r2 − радиусы оснований шарового слоя, S1, S2 − площади этих оснований.

13. Объем шарового слоя
V=πh(3r21+3r22+h2)6,
где r1, r2 − радиусы оснований шарового слоя, h − его высота.

14. Шаровым сектором называется часть шара, состоящая из шарового сегмента и конуса с вершиной в центре шара и основанием, совпадающим с основанием шарового сегмента. Здесь подразумевается, что шаровой сегмент меньше полушара.

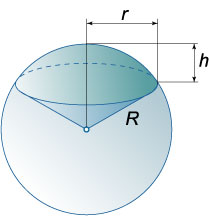
15. Площадь полной поверхности шарового сектора
S=πR(2h+r),
где h − высота соответствующего шарового сегмента, r − радиус основания шарового сегмента (или конуса), R − радиус шара.

16. Объем шарового сектора
V=2πR2h3

• -- ---. Понятие цилиндра О О 1 a b А А 1 образующая Основание цилиндра Цилиндрическая поверхность Ось цилиндра r Радиус цилиндра
• 3.
• Тело, ограниченное цилиндрической поверхностью и двумя кругами с границами, называется цилиндром.
• Цилиндрическая поверхность – боковая поверхность цилиндра, а круги - основания цилиндра.
• Длина образующей – высота цилиндра.
• Цилиндр можно получить вращением прямоугольника вокруг одной из его сторон
• 4. Сечения цилиндра:
• Если секущая плоскость проходит через ось цилиндра, то сечение представляет собой прямоугольник, две стороны которого образующие, а две другие – диаметры основания цилиндра.
• Такое сечение называется осевым.
• Сечение является кругом, если секущая плоскость перпендикулярна к оси цилиндра
• 5. Площадь поверхности цилиндра:
• За площадь боковой поверхности цилиндра принимается площадь её развёртки
• Площадь полной поверхности цилиндра – сумма площадей боковой поверхности и двух оснований:
• S = 2 П r(r + h)

S бок = 2п rh

• 6. Пусть дана плоскость
• 7. Проведем прямую, перпендикулярно этой плоскости, а на плоскости окружность с центром в точке пересечения этой прямой с плоскостью Выберем на прямой произвольную точку и соединим ее отрезками с каждой точкой окружности
• 8. Выберем на прямой произвольную точку и соединим ее отрезками с каждой точкой окружности Проведем прямую, перпендикулярно этой плоскости, а на плоскости окружность с центром в точке пересечения этой прямой с плоскостью
• 9. Поверхность, состоящая из всех таких отрезков, называется конической поверхностью Выберем на прямой произвольную точку и соединим ее отрезками с каждой точкой окружности
• 10. Поверхность, состоящая из всех таких отрезков, называется конической поверхностью Выберем на прямой произвольную точку и соединим ее отрезками с каждой точкой окружности
• 11. Поверхность, состоящая из всех таких отрезков, называется конической поверхностью
• 12. Тело, состоящее из конической поверхности и круга, граница которого принадлежит конической поверхности, называется круговым конусом
• 13.
• Конус в переводе с греческого «konos» означает «сосновая шишка». С конусом люди знакомы с глубокой древности. В 1906 году была обнаружена книга Архимеда (287-212 гг. до н.э.) «О методе», в которой дается решение задачи об объеме общей части пересекающихся цилиндров. Архимед приписывает честь открытия этого принципа Демокриту (470-380 гг. до н.э.) – древнегреческому философу-материалисту. С помощью этого принципа Демокрит получил формулу для вычисления объема пирамиды и конуса.
• Много сделала для геометрии школа Платона (428-348 гг. до н.э.). Платон был учеником Сократа (470-399 гг. до н.э.). Он в 387 г. до н.э. основал в Африке Академию, в которой работал 20 лет. Каждый, входящий в Академию, читал надпись: «Пусть сюда не входит никто, не знающий геометрии». Школе Платона, в частности, принадлежит: а) исследование свойств призмы, пирамиды, цилиндра и конуса; б) изучение конических сечений.
• Большой трактат о конических сечениях был написан Аполлонием Пергским (260-170 гг. до н.э.) – учеником Евклида (III в. До н.э.), который создал великий труд из 15 книг под названием «Начала». Эти книги издаются и по сей день, а в школах Англии по ним учатся до сих пор.
• 14. Основные сведения
• R – радиус основания
• H – высота
• L – образующая
• S полн. = π RH(R+H)

L R H

• 15. Практическое применение
• конические детали в машинах и механизмах;
• в автомобилях, танках, бронетранспортёрах – конические шестерни;
• носовая часть самолётов и ракет.