 |
Цилиндрический изгиб равномерно нагруженной прямоугольной пластины жестко опертой по краям, опирающейся всей поверхностью на упругое основание.
|
|
|
|
Введение.
Понятие о сплошном упругом основании.
Модель Винклера.
В инженерной практике часто встречаются конструкции, опирающиеся по всей длине или площади на сплошное основание, которое может упруго деформироваться под действием приложенной к нему нагрузки. К таким конструкциям относятся, например, фундаменты зданий и гидротехнических сооружений, аэродромные и дорожные покрытия и т. п., опирающиеся на различного рода грунтовые и скальные основания. Конструкции на упругом основании могут иметь также жесткие опоры.
 При расчете конструкций на упругом основании необходимо определить реактивный отпор со стороны основания на конструкцию. Реактивный отпор представляет собой поперечную нагрузку, распределенную по длине или площади конструкции.
При расчете конструкций на упругом основании необходимо определить реактивный отпор со стороны основания на конструкцию. Реактивный отпор представляет собой поперечную нагрузку, распределенную по длине или площади конструкции.
Рассмотрим, например, работу балки, свободно лежащую на упругом основании. Суммарная распределенная нагрузка на балку равна
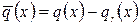 ,
,
где  - внешняя нагрузка на балку, а
- внешняя нагрузка на балку, а  - реактивный отпор основания (рис. а).
- реактивный отпор основания (рис. а).
Внешняя нагрузка на балку, как правило, всегда известна. Задача, таким образом, сводится к определению реактивного отпора. Эта задача не может быть решена с помощью уравнений статики. Например, для свободно лежащей балки уравнения статики позволяют определить только величину равнодействующей реактивного отпора основания и положение линии ее действия. Закон распределения реактивного отпора по длине балки остается при этом неизвестным.
Для решения такой задачи необходимо ввести предположение о зависимости между реактивным отпором и осадкой поверхности основания  (рис. б). Эта зависимость характеризует расчетную схему или модель основания. Учеными и инженерами в разное время предложено несколько моделей упругого основания. Наиболее простой и широко применяемой на практике является модель, предложенная немецким ученым Е. Винклером. В этой модели зависимость между реактивным отпором основания и осадкой его поверхности предполагается линейной и в задачах расчета балок на упругом основании записывается в следующем виде:
(рис. б). Эта зависимость характеризует расчетную схему или модель основания. Учеными и инженерами в разное время предложено несколько моделей упругого основания. Наиболее простой и широко применяемой на практике является модель, предложенная немецким ученым Е. Винклером. В этой модели зависимость между реактивным отпором основания и осадкой его поверхности предполагается линейной и в задачах расчета балок на упругом основании записывается в следующем виде:
|
|
|
 ,
,
где b – ширина подошвы балки и k – коэффициент, характеризующий жесткость основания и называемый коэффициентом постели.
Этот коэффициент определяется экспериментально и имеет размерность силы, отнесенной к единице длины в третьей степени, например Н/см3.
Значения коэффициента жесткости (коэффициента постели) некоторых грунтовых и скальных оснований приведены в таблице 1.
Таблица 1
| №№ пп | Материал основания | k Н/см3 |
| Песок свеженасыпанный Глина мокрая, размягченная | 
| |
| Песок слежавшийся Гравий насыпной Глина влажная | 
| |
| Песок и гравий плотно слежавшиеся Щебень Глина малой влажности | 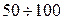
| |
| Грунт песчано-глинистый искусственно уплотненный Глина твердая | 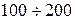
| |
| Известняк, песчаник, мерзлота | 
| |
| Твердая скала | 
|
С физической точки зрения модель  Е. Винклера может быть представлена множеством несвязанных между собой одинаковых упругих пружин, опирающихся на абсолютно жесткое основание.
Е. Винклера может быть представлена множеством несвязанных между собой одинаковых упругих пружин, опирающихся на абсолютно жесткое основание.
В большинстве задач принимается, что пружины могут работать как на сжатие, так и на растяжение, что характеризует двустороннюю связь между балкой и основанием
Деформация упругого основания, соответствующего модели Винклера, происходит только в области, приложенной к нему нагрузки. Это достаточно хорошо отражает реальные свойства рыхлых и несвязных оснований.
Для плотных и, тем более, скальных оснований модель Винклера не соответствует действительному характеру деформации основания, которая происходит и за пределами области приложения нагрузки. Существуют другие модели упругого основания (например, модель с двумя коэффициентами постели, модель упругого полупространства и т. п.), которые позволяют учитывать работу основания за пределами области приложенных нагрузок. Однако расчет балок и других конструктивных элементов с использованием таких моделей достаточно сложен.
|
|
|
Цилиндрический изгиб равномерно нагруженной прямоугольной пластины жестко опертой по краям, опирающейся всей поверхностью на упругое основание.
 Рассмотрим изгиб длинной прямоугольной пластины, равномерно нагруженной, опирающейся всей своей поверхностью на упругое основание и жестко опертой по краям (рис. 1.1). Вырезав из пластины элементарную балку – полосу, ее можно рассматривать как балку на упругом основании. При этом полагают, что балка-полоса уложена на постель из материала, способного сопротивляться как силам, действующим вниз, так и силам, действующим вверх. Положив, что реакция основания в некоторой произвольной точке пластины пропорциональна ее прогибу w в этой точке (модель Винклера) и воспользовавшись уравнением
Рассмотрим изгиб длинной прямоугольной пластины, равномерно нагруженной, опирающейся всей своей поверхностью на упругое основание и жестко опертой по краям (рис. 1.1). Вырезав из пластины элементарную балку – полосу, ее можно рассматривать как балку на упругом основании. При этом полагают, что балка-полоса уложена на постель из материала, способного сопротивляться как силам, действующим вниз, так и силам, действующим вверх. Положив, что реакция основания в некоторой произвольной точке пластины пропорциональна ее прогибу w в этой точке (модель Винклера) и воспользовавшись уравнением
 ,
,
после двукратного его дифференцирования получим
 . (1.1)
. (1.1)
Здесь q – интенсивность действующей на пластину нагрузки, а k – реакция основания на единицу площади при прогибе, равном единице (коэффициент жесткости упругого основания - коэффициент постели).
Используя обозначение
 (1.2)
(1.2)
общее решение уравнения (1.1) можно представить в следующем виде:
 , (а)
, (а)
где первые четыре члена представляют решение однородного дифференциального уравнения, а последний член – частное решение, зависящее от характера внешней нагрузки.
Из условий на концах балки-полосы надлежит определить четыре постоянных интегрирования. В рассматриваемом случае прогиб симметричен относительно середины полосы. Расположим поэтому оси координат в соответствии с рис. 1.1. При принятой системе координат члены выражения (а) с коэффициентами С2 и С3 меняют знак при замене x на – x и, следовательно, граничные условия выполняются, если С2 =С3 =0.
Тогда выражение (а) принимает вид:
 (б)
(б)
Постоянные С1 и С4 находим из условия, что на конце 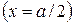 как прогиб, так и изгибающий момент полосы равны нулю. Поэтому
как прогиб, так и изгибающий момент полосы равны нулю. Поэтому
|
|
|
 . (в)
. (в)
Подставив в выражение (в) значение w из выражения (б), получим
 . (г)
. (г)
Найдем вторую производную от прогиба..


или
 . (д)
. (д)
Подставим значение второй производной во второе граничное условие.
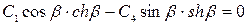 . (е)
. (е)
Рассмотрим совместно граничные условия (г) и (е).




Упростим выражение
 .
.
Окончательно получим выражения для С1 и С4 в виде:
 (ж)
(ж)
Подставив значения произвольных интегрирования в выражение (б), получим:

С учетом (1.2) выражение для прогиба имеет вид:
 (1.3)
(1.3)
Определим прогиб в середине полосы  .
.
 (1.4)
(1.4)
где
 . (1.5)
. (1.5)
Для получения углов поворота пластины, дифференцируем выражение (1.3).
 (з)
(з)
Определим угол поворота края пластины  .
.


 ,
,
 , (1.6)
, (1.6)
где
 . (1.7)
. (1.7)
Изгибающий момент в произвольном сечении балки-полосы получим из уравнения
 .
.

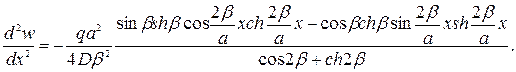
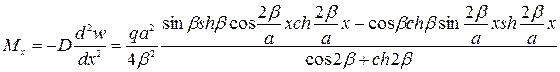 . (1.8)
. (1.8)
Для середины балки-полосы 
 . (1.9)
. (1.9)
где
 . (1.10)
. (1.10)
Перечную силу в произвольном сечении балки-полосы получим из уравнения 
 ,
,
или, с учетом (1.5) и (1.10):
 . (1.11)
. (1.11)
Для левого края балки-полосы  :
:
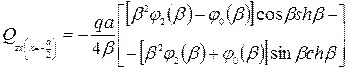 . (1.12)
. (1.12)
Подставив (1.5) и (1.10) в (1.3) формулу для прогиба приведем к виду:
 (1.13)
(1.13)
|
|
|


