 |
Лекция 11. Экстремальные задачи на метрических пространствах.
|
|
|
|
Основные теоремы.
Дан булев куб размерности n с расстояние Хэмминга. В нем нужно разместить M точек, попарные расстояния между которыми не меньше. Пусть A(n,d) это максимальное значение M при таком размещении. Задача состоит в нахождении A(n,d) и оценок для него.
Лемма. Пусть есть множество V= (α1… αk), 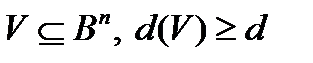 . Также есть множество V’= (β1… βS),
. Также есть множество V’= (β1… βS), 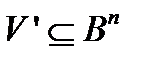 и для любых x, y
и для любых x, y 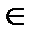 V’:
V’:  . Тогда множества
. Тогда множества 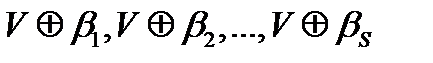 не пересекаются.
не пересекаются.
Доказательство. От противного. Если два множества пересекаются, то существуют четыре вектора, для которых справедливо соотношение:

где 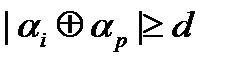 ,
, 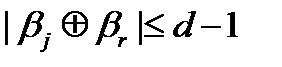 . Получило противоречие.
. Получило противоречие.
Лемма доказана.
Теорема. (Граница Хемминга) Справедливо соотношение:
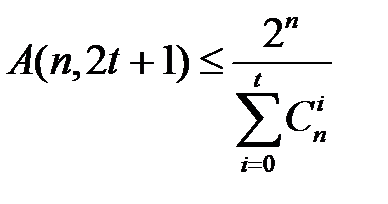
Доказательство.
Пусть V= (α1… αk) – наш код, V’ = 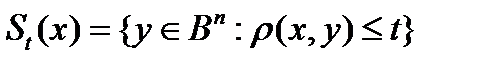 – шар радиуса t, тогда в этом шаре расстояние между двумя любыми точками не превосходит ρ
– шар радиуса t, тогда в этом шаре расстояние между двумя любыми точками не превосходит ρ 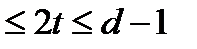 .
.
Из леммы следует, что множества вида V  y, где y
y, где y 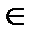 V’, не пересекаются, но тогда
V’, не пересекаются, но тогда
 .
.
По определению  и получим искомое неравенство.
и получим искомое неравенство.
Теорема доказана.
Теорема (Граница Джоши). Справедливо соотношение:
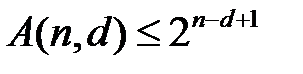 .
.
Доказательство. Пусть V – множество векторов с попарным расстоянием не меньше расстоянием d, 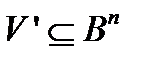 , V’ – множество всех векторов y, у которых первые d-1 компонент произвольные, а остальные нули, т.е y=
, V’ – множество всех векторов y, у которых первые d-1 компонент произвольные, а остальные нули, т.е y= 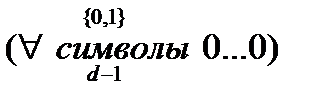 . Тогда
. Тогда  , для любых x, y
, для любых x, y 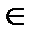 V’:
V’:  .
.
Снова из леммы получаем
 .
.
Теорема доказана.
Теорема (Варшамова-Гильберта). Справедливо соотношение:
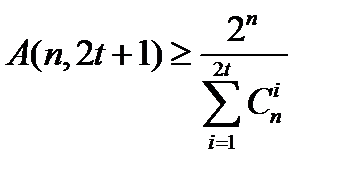 .
.
Доказательство. Рассмотрим простую геометрическую аналогию. Пусть дан отрезок [a,b]. Мы произвольным образом поочередно размещаем на нем отрезки длины d<(b-a) так, чтобы они не пересекались. Пусть мы разместили k таких отрезков, а (k+1)-й уже не помещается. После этого мы, оставляя на месте центры размещенных отрезков, увеличиваем их вдвое на одинаковую величину в обе стороны. После этой операции на отрезке не останется пустого места, ведь, если бы оно было, то от любой точки на этом пустом месте, до центра одного из соседних размещенных отрезков было бы расстояние, большее 2d, а это противоречит тому, что (k+1)-й отрезок ранее уже не мог быть размещен.
|
|
|
На этом факте и основано доказательство теоремы. Вместо отрезка берем булев куб B n и размещаем в нем шары 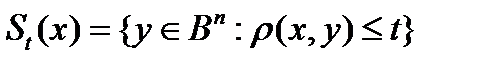 . Таким образом будет построено множество векторов V*, которые соответствуют центрам размещенных шаров.
. Таким образом будет построено множество векторов V*, которые соответствуют центрам размещенных шаров.
Построим V* следующим образом:
Итерации:
x 1 → V*
x 2 → V* \ St (x’)
…
p) xp → V* \ 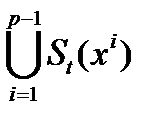
В какой-то момент очередной шар уже не поместится. Расстояние между любыми точками таким образом построенной конструкции равняется 2 t, а шары радиуса 2 t с центрами в этих точках покроют весь булев куб. Так как они могут пересекаться, то суммарное количество точек в этих шарах будет не меньше мощности куба, откуда и следует неравенство в теореме.
Теорема доказана.
Теорема (Плоткина). При условии, что 2d>n cправедливо соотношение:
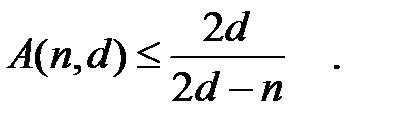
Доказательство. Рассмотрим множество булевых векторов  , попарные расстояния между которыми не менее d. Построим таблицу.
, попарные расстояния между которыми не менее d. Построим таблицу.
 , где k 1, k 2,…, k n – количество единиц в столбце.
, где k 1, k 2,…, k n – количество единиц в столбце.
Рассмотрим сумму расстояний между всеми векторами множества.

Здесь каждое расстояние подсчитано 2 раза. Тогда 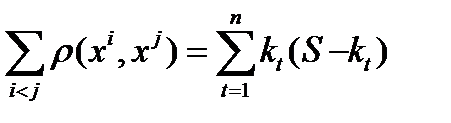 .
.
Заметим, что max x (S- x) достигается при x = S /2. Воспользуемся этим. Тогда справедливо соотношение:
 (11.1)
(11.1)
Кроме того, по условию 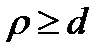 . Поставим это неравенство в (11.1):
. Поставим это неравенство в (11.1): 
 . Отсюда следует nS≥2d(S-1) и
. Отсюда следует nS≥2d(S-1) и
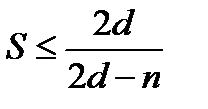 .
.
Теорема доказана.
Сводка результатов.
Рассмотренные в этих теоремах конструкции имеют разнообразное применение в комбинаторном анализе. Так как ниже будем их применять при передачи информации по каналу с шумом, то используем терминологию, принятую в теории кодирования.
Пусть Bn - булев куб размерности n.
|
|
|
Определение. Кодом C называется произвольное подмножество 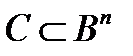 .
.
Пусть M – мощность множества C. Элементы этого подмножества будем называть кодовыми словами.
Пусть k - минимальное целое, такое что M≤2k. (Ниже будет рассмотрен важный класс кодов, где всегда M=2k).
Определение. Кодовой скоростью называется число  .
.
Определение. Кодовым расстоянием называется число 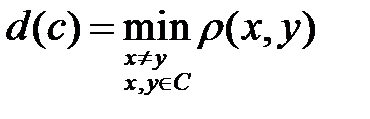 .
.
Так как расстояние Хемминга  - это количество различных бит в x и y, а
- это количество различных бит в x и y, а
|| x || - количество единиц в  (норма или вес x). Тогда очевидно, что
(норма или вес x). Тогда очевидно, что
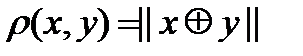 .
.
Определение. (n, M, d)-код – это код C, такой, что | C | = M, C = { xi }, xi  Bn, d (C) = d.
Bn, d (C) = d.
Сведем полученные в приведенных выше теоремах результаты на один график, по координатам которого даны отношения k/n и d/2n. (Этот график можно найти в любой книге по теории кодов, исправляющих ошибки, например, в [7]).
| k/n |
| П |

| 0.156 |
| 1 |
| 0.9 |
| 0.8 |
| 0.7 |
| 0.6 |
| 0.5 |
| 0.4 |
| 0.3 |
| 0.2 |
| 0.1 |
| 0.4 |
| 0.3 |
| 0.2 |
| 0.1 |
| 0 |
| 0.5 |
| d/ 2 n |
| Х |
| ВГ |
Соответствующие кривые, вытекающие из теорем, обозначены: ВГ- Теорема Варшамова-Гильберта, П- Теорема Плоткина, Х - Теорема Хэмминга.
Комментарий к графику.
Из графика видно, что при постоянном отношении k/n и росте размерности куба границы для отношения d/n стремятся константе, не зависящей от этой размерности.
(n,M,d)-коды существуют только для тех значений параметров, которые лежат в заштрихованной области. Однако, не для любой точки в этой области (а каждой такой точке соответствует фиксированная тройка параметров n,M,d) известен (построен) (n,M,d)-код.
Ниже будут рассмотрены несколько примеров известных кодов, в частности коды Хэмминга и коды Боуза-Чоудхури-Хоквингема (БЧХ-коды). Они при больших скоростях передачи лежат на границе Хэмминга и являются оптимальными. Для малых скоростей БЧХ-коды лежат на границе Плоткина.
При средних скоростях для БЧХ-кодов отношение d/n стремится к 0, когда n неограниченно растет.
Неизвестны коды, для которых d/n остается конечным при росте n и фиксированном k/n, хотя граница Варшамова-Гильберта дает основание считать, что такие коды должны быть.
В следующих лекциях будет доказана вторая теорема Шеннона (теорема Шеннона для канала с шумом). Из нее следует, что при любой скорости k/n, меньшей пропускной способности канала, существуют коды, вероятность ошибки декодирования в которых может быть сделана сколь угодно близкой к нулю.
|
|
|
В целом, существующие коды, с теоретической точки зрения, далеки от оптимальных, поэтому теория кодирования до сих пор дает возможность исследователям получать интересные результаты.
Упражнения.
Пусть A(n,d) – максимальное число точек в коде из Bn с минимальным расстоянием d. Пусть B(n,d) – максимальное число точек в коде из Bn такое, что расстояние между любой парой не больше d.
1. Доказать неравенство  .
.
2. Проверить существование (8,12,3)-кода. Проверить существование (12,200,3)-кода.
3. При каких параметрах граница Джоши лучше границы Хэмминга?
4. Доказать соотношения:
a)  ;
;
b)  ;
;
c) 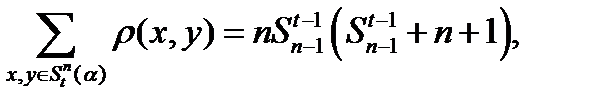 где
где 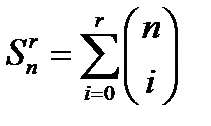 .
.
|
|
|


