 |
Электромагнитные волны в ферромагнетике при экваториальном (поперечном) намагничивании
|
|
|
|
Теоретическое изучение нечетных экваториальных МОЭ проводилось в целом ряде работ [8,9,16,27,32,33,34 и др]. В настоящей главе использованы, в основном, результаты работ [8,16,27,32], в которых развита наиболее полная теория нечетных экваториальных МОЭ как в отраженном, так и в прошедшем свете для бигиротропной ферромагнитной среды.
Феноменологическая теория МОЭ основана на уравнениях макроскопической электродинамики, включающих уравнения поля, материальные уравнения среды я граничные условия [2]. В качестве исходной выбирается система уравнений Максвелла
rot  = -
= - 
 , diw
, diw  = 0,
= 0,
(1.1)
rot 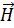 =
= 
 , diw
, diw  = 0,
= 0,
где  и
и 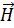 - напряженности электрического и магнитного полей,
- напряженности электрического и магнитного полей,  и
и  – вектора электрической и магнитной индукции. На поверхности раздела двух сред эти поля удовлетворяют граничным условиям
– вектора электрической и магнитной индукции. На поверхности раздела двух сред эти поля удовлетворяют граничным условиям
[  x
x 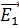 ] = [
] = [  x
x  ], [
], [  x
x  ] = [
] = [  x
x 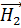 ], (1.2)
], (1.2)
( - орт нормали к границе раздела), которые выражают непрерывность тангенциальных составляющих напряженностей электрического и магнитного полей.
- орт нормали к границе раздела), которые выражают непрерывность тангенциальных составляющих напряженностей электрического и магнитного полей.
Система линейных однородных уравнений (1.1) имеет решения в форме монохроматических плоских волн вида
 (t,
(t, 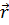 ) =
) =  ∙ exp i (wt -
∙ exp i (wt - 

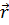 ), (1.3)
), (1.3)
где t - время, 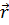 - координата, w - частота, С - скорость света в вакууме. Амплитуда
- координата, w - частота, С - скорость света в вакууме. Амплитуда  плоской волны определяет состояние её поляризации (в общем случае эллиптической) и носит название вектора поляризации. Вектор рефракции
плоской волны определяет состояние её поляризации (в общем случае эллиптической) и носит название вектора поляризации. Вектор рефракции  =
=  ’- i
’- i  ” связан с комплексным показателем преломления n плоской волны соотношением
” связан с комплексным показателем преломления n плоской волны соотношением
n =  =
=  . (1.4)
. (1.4)
Действительная часть вектора рефракции  ’определяет направление распространения фронта волны, а мнимая
’определяет направление распространения фронта волны, а мнимая  ” - направление её затухания. Волна (1.3) однородна при условии, что вектора
” - направление её затухания. Волна (1.3) однородна при условии, что вектора  ’ и
’ и  ” коллинеарны. Плоская волна является поперечной, если ее вектор амплитуды ортогонален вектору рефракции, т.е.
” коллинеарны. Плоская волна является поперечной, если ее вектор амплитуды ортогонален вектору рефракции, т.е. 
 = 0.
= 0.
|
|
|
Для полей в форме плоских волн (1.3) уравнения Максвелла (1.1) принимают вид
 = [
= [  x
x  ],
], 
 = 0,
= 0,
(1.5)
 = - [
= - [  x
x 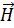 ],
], 
 = 0,
= 0,
Вектора индукции  и
и  связаны с напряженностями полей материальными уравнениями
связаны с напряженностями полей материальными уравнениями
 =
= 
 ,
,  =
= 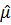
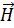 , (1.6)
, (1.6)
где  и
и 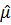 - тензоры диэлектрической и магнитной проницаемости среды. Подстановка (1.6) в (1.5) приводит к волновому уравнению
- тензоры диэлектрической и магнитной проницаемости среды. Подстановка (1.6) в (1.5) приводит к волновому уравнению
 + [
+ [  x
x 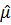 -1 [
-1 [  x
x  ]] = 0, (1.7)
]] = 0, (1.7)
которое определяет вектора поляризации  волн, распространяющихся в среде, описываемой тензорами
волн, распространяющихся в среде, описываемой тензорами  и
и 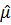 . Отметим, что уравнение (1.7) определяет вектор поляризации волны лишь с точностью до произвольного скалярного множителя. Как известно [35], умножение на такой множитель не изменяет состояние поляризации волны. Таким образом, поляризация плоской волны с заданным вектором рефракции
. Отметим, что уравнение (1.7) определяет вектор поляризации волны лишь с точностью до произвольного скалярного множителя. Как известно [35], умножение на такой множитель не изменяет состояние поляризации волны. Таким образом, поляризация плоской волны с заданным вектором рефракции  зависит целиком от структуры тензоров
зависит целиком от структуры тензоров  и
и 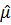 . Система линейных однородных уравнений (1.7) относительно компонент Ei имеет отличное от нуля решение в том случае, если определитель этой системы равен нулю. Из этого условия находятся показатели преломления волн.
. Система линейных однородных уравнений (1.7) относительно компонент Ei имеет отличное от нуля решение в том случае, если определитель этой системы равен нулю. Из этого условия находятся показатели преломления волн.
Ограничимся рассмотрением однородной и изотропной ферромагнитной среды, намагниченной до состояния насыщения. В системе координат, в которой ось Z выбрана вдоль вектора намагниченности, тензоры диэлектрической и магнитной проницаемости ферромагнетика записывается в виде [1]
 (w) =
(w) = 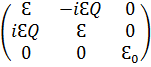 ;
;  (1.8)
(1.8)
Величины Q и M, определяемые выражение:
Q = i  , M = i
, M = i 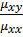 (1.9)
(1.9)
называются соответственно первым и вторым магнитооптическими параметрами и являются нечетными функциями намагниченности. Проницаемости Ɛ =  , Ɛ0 =
, Ɛ0 =  , μ =
, μ =  , μ0 =
, μ0 =  , зависят только от четных степеней намагниченности, и их разности Ɛ0 – Ɛ, μ0 – μ, вызывают слабые (на фоне нечетных эффектов) эффекты высокочастотной магнитной анизотропии. Отличные от нуля величины
, зависят только от четных степеней намагниченности, и их разности Ɛ0 – Ɛ, μ0 – μ, вызывают слабые (на фоне нечетных эффектов) эффекты высокочастотной магнитной анизотропии. Отличные от нуля величины  приводят к возникновению МОЭ, которые принято называть гироэлектрическими. Аналогично, эффекты, которые связаны е неравенством нулю недиагональной компоненты
приводят к возникновению МОЭ, которые принято называть гироэлектрическими. Аналогично, эффекты, которые связаны е неравенством нулю недиагональной компоненты  тензора магнитной проницаемости, называют гиромагнитными. Среда, у которой в некотором интервале частот одновременно
тензора магнитной проницаемости, называют гиромагнитными. Среда, у которой в некотором интервале частот одновременно 
 0 и
0 и 
 0 называется бигиротропной.
0 называется бигиротропной.
|
|
|
Рассмотрим волны в ферромагнетике, вектор рефракции которых ортогонален вектору намагниченности. В этом случае говорят, что по отношению к распространяющейся волне ферромагнетик экваториально, или поперечно, намагничен. Если  - орт намагниченности, то при экваториальном
- орт намагниченности, то при экваториальном 
 = 0, или, в выбранной системе координат, где
= 0, или, в выбранной системе координат, где  = (0,0,1), nz = 0. Экваториальное намагничивание имеет место, например, при наклонном падении световой волны на образец, когда последний намагничен перпендикулярно плоскости падения света. Решение волнового уравнения (1.7) с учетом выражений (1.8) и условия
= (0,0,1), nz = 0. Экваториальное намагничивание имеет место, например, при наклонном падении световой волны на образец, когда последний намагничен перпендикулярно плоскости падения света. Решение волнового уравнения (1.7) с учетом выражений (1.8) и условия 
 = 0, дает следующие результаты.
= 0, дает следующие результаты.
При экваториальном намагничивании в изотропной ферромагнитной среде распространяются две нормальные плоские волны моды с показателями преломления n1 и n2, квадраты которых равны
 = Ɛ0μ ∙ (1- M2),
= Ɛ0μ ∙ (1- M2),  = Ɛμ0 ∙ (1- Q2). (1.10)
= Ɛμ0 ∙ (1- Q2). (1.10)
Соответствующие вектора поляризации волн, единичные амплитуды напряженностей электрического ( ) и магнитного (
) и магнитного ( ) поля даются выражениями:
) поля даются выражениями:
 1 =
1 =  ,
,
 1 =
1 = 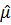 -1[
-1[  1∙
1∙  1] =
1] =  ([
([  1∙
1∙  ] - iM
] - iM  1),
1),
(1.11)
 2 =
2 =  ([
([  2∙
2∙  ] - iQ
] - iQ  2),
2),
 2 =
2 = 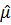 -1[
-1[  2∙
2∙  2] = -
2] = - 
 ,
,
где  - орт намагниченности,
- орт намагниченности,  1 и
1 и  2 - вектора рефракции первой и второй волны.
2 - вектора рефракции первой и второй волны.
Анализ формул (1.10) и (l.11) позволяет сделать некоторые заключения об общем характере МОЭ при экваториальном намагничивании. Прежде всего, как видно из (l.10), показатели преломления волн зависят только от четных степеней намагниченности. Поэтому нечетные эффекты, обусловленные двойным магнитным лучепреломлением, в такой геометрии отсутствуют. С другой стороны, вектора поляризации  1 и
1 и  2 содержат нечетные по намагниченности продольные вдоль векторов рефракции
2 содержат нечетные по намагниченности продольные вдоль векторов рефракции  1 и
1 и  2 составляющие. Именно наличие этих продольных составляющих у векторов поляризации волн является причиной возникновения нечетных экваториальных эффектов. Наконец, существует еще одна отличительная особенность волн при экваториальном намагничивании. Она состоит в том, что характеристики (показатель преломления n1 и вектора поляризации) первой волны зависят от величины μxy, но не зависят от Ɛxy и, наоборот, характеристики второй волны зависят только от величины Ɛxy. Указанная особенность приводит к тому, что если под действием падающего света в ферромагнетике возбуждается первая волна, то возникающие МОЭ имеют чисто гиромагнитное происхождение, а при возбуждении второй волны возникает только гироэлектрические эффекты. Таким образом, при экваториальном намагничивании существуют МОЭ, позволяющие раздельно изучать гироэлектрические и гиромагнитные свойства ферромагнитной среды.
2 составляющие. Именно наличие этих продольных составляющих у векторов поляризации волн является причиной возникновения нечетных экваториальных эффектов. Наконец, существует еще одна отличительная особенность волн при экваториальном намагничивании. Она состоит в том, что характеристики (показатель преломления n1 и вектора поляризации) первой волны зависят от величины μxy, но не зависят от Ɛxy и, наоборот, характеристики второй волны зависят только от величины Ɛxy. Указанная особенность приводит к тому, что если под действием падающего света в ферромагнетике возбуждается первая волна, то возникающие МОЭ имеют чисто гиромагнитное происхождение, а при возбуждении второй волны возникает только гироэлектрические эффекты. Таким образом, при экваториальном намагничивании существуют МОЭ, позволяющие раздельно изучать гироэлектрические и гиромагнитные свойства ферромагнитной среды.
|
|
|
|
|
|


