 |
Решение задачи № 3. Утверждение 1. ( О структуре общего решения неоднородного уравнения). I. Нахождение общего решения линейного однородного уравнения с постоянными коэффициентами (метод Эйлера)
|
|
|
|
Решение задачи № 3
Найдем частное решение уравнения
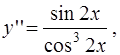(1)
удовлетворяющее начальным условиям
(2)
Данное уравнение является «простейшим» уравнением второго порядка, правая часть которого зависит только от независимой переменной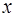 
, т. е. уравнением вида
Предполагается, что функция 
непрерывна в некотором интервале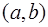 
. Тогда для простейшего уравнения справедлива теорема существования и единственности решения (см. [2] и [4]).
Для уравнения (1)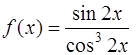 
и с учетом начальных условий (2) мы выбираем интервал 
.
Тогда на плоскости 
в интервале 
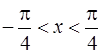существует единственная интегральная кривая уравнения (1), проходящая через точку с координатами 
и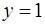 
, при этом тангенс угла наклона касательной в этой точке равен нулю (геометрический смысл начальных условий (2)).
Найдем решение задачи Коши (1), (2).
Учитывая, что
и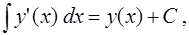 
проинтегрируем обе части уравнения (1) по переменной 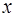. В результате получим
Для вычисления интеграла сделаем замену переменной 
.
Отсюда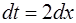 
, 
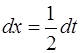и
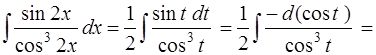
Таким образом,
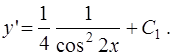(3)
Найдем значение постоянной интегрирования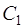 
, используя начальное условие 
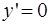при . Учитывая, что 
, получаем
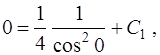
и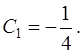 
Подставим значение 
в уравнение (3)
(4)
Интегрируя обе части уравнения (4) по переменной 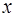, получим
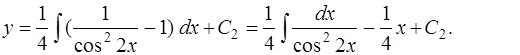
Для вычисления интеграла вновь сделаем замену переменной и .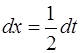
Тогда
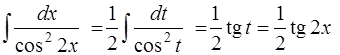
и, следовательно,
Найдем значение постоянной интегрирования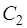 
, используя второе начальное условие 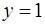при . Учитывая, что 
, получаем
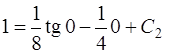и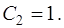 
Отсюда искомое частное решение уравнения (1), удовлетворяющее начальным условиям (2), запишется в виде
|
|
|
Ответ. Решением задачи Коши (1), (2) является функция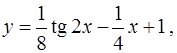 
определенная на интервале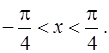 
В задачах 4 и 5 даны линейные дифференциальные уравнения второго порядка с постоянными коэффициентами и со специальной правой частью.
Уравнение вида
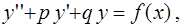(1)
где 
и 
– вещественные числа, а – функция непрерывная на некотором промежутке, называется линейным уравнением второго порядка с постоянными коэффициентами.
Функция
(2)
называется функцией специального вида.
Комплексные числа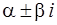 
будем называть контрольными числами.
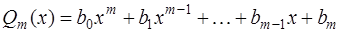
–многочлены степени 
и 
.
Функция специального вида (2) определена при всех 
Уравнение (1) называется неоднородным, если функция не равна тождественно нулю. Если же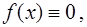 
то уравнение (1) принимает вид
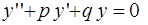(3)
и называется однородным.
Если левые части однородного и неоднородного уравнений совпадают, то в этом случае однородное уравнение называется соответствующим данному неоднородному.
Имеет место следующее утверждение (см. [2], [4] и [5]).
Утверждение 1. ( О структуре общего решения неоднородного уравнения).
Если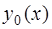 
– общее решение однородного уравнения (3), а 
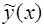– какое-либо частное решение неоднородного уравнения (1), то
(4)
есть общее решение неоднородного уравнения (1).
Отсюда следует, что построение общего решения неоднородного уравнения состоит из двух этапов. Сначала нужно найти общее решение 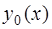соответствующего однородного уравнения, а затем найти какое-либо частное решение 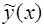неоднородного уравнения.
I. Нахождение общего решения линейного однородного уравнения с постоянными коэффициентами (метод Эйлера)
Определение. Будем говорить, что два решения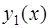 
и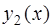 
линейного однородного уравнения (3) линейно независимы на промежутке 
, если их отношение 
не равно тождественно константе.
|
|
|
Тогда имеет место следующее утверждение.
Утверждение 2. ( О структуре общего решения однородного уравнения).
Есл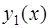и и 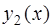– два линейно независимых решения уравнения (3), то их линейная комбинация
(5)
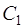где и 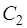– произвольные постоянные, есть общее решение линейного однородного уравнения (3).
Решение уравнения (3)
где и – вещественные числа, будем искать в виде
(6)
Постоянная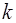 
подлежит определению.
Так как 
и 
, то подстановка полученных выражений производных в уравнение (3) приводит к равенству
Так как 
, то последнее равенство выполняется, если
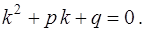(7)
Таким образом, функция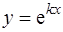 
является решением дифференциального уравнения (3), если постоянная 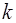является корнем квадратного уравнения (7).
|
|
|
