 |
I. Дифференциальные уравнения, допускающие понижение порядка.
|
|
|
|
Основные понятия и определения. Теорема и задача Коши.
Дифференциальные уравнения, порядок которых выше первого, называются дифференциальными уравнениями высших порядков. В общем виде эти уравнения записывают
F (x, y, y¢,..., y ( n )) = 0, п >1,
или в нормальной форме
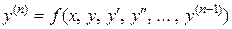 .
.
Дифференциальные уравнения высших порядков рассмотрим на примере дифференциальных уравнений второго порядка:
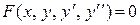 , (2. 1)
, (2. 1)
которые в нормальной форме имеют вид
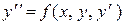 . (2. 2)
. (2. 2)
Задача Коши для дифференциального уравнения второго порядка формулируется следующим образом:
 Найти решение
Найти решение  дифференциального уравнения (2.2), удовлетворяющее начальным условиям
дифференциального уравнения (2.2), удовлетворяющее начальным условиям
 (2.3)
(2.3)
Систему (2.3) называют системой начальных условий.
Условия разрешимости задачи Коши для дифференциального уравнения 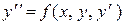 определяет следующая теорема существования и единственности:
определяет следующая теорема существования и единственности:
Теорема 2.1 (Коши)
Если функция 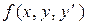 и ее частные производные
и ее частные производные  и
и 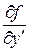 определены и непрерывны в некоторой области D изменения переменных х, у, у ¢, то для любой внутренней точки
определены и непрерывны в некоторой области D изменения переменных х, у, у ¢, то для любой внутренней точки 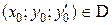 существует единственное решение
существует единственное решение  дифференциального уравнения
дифференциального уравнения  , удовлетворяющее условиям
, удовлетворяющее условиям 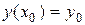 ,
, 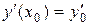 .
.
Как и в случае дифференциального уравнения первого порядка, из теоремы 2.1 следует:
1) каждой точке М0 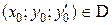 соответствует единственное решение
соответствует единственное решение  уравнения, определенное в некоторой окрестности точки
уравнения, определенное в некоторой окрестности точки 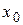 ;
;
2) в области D, в которой выполняются условия теоремы, уравнение 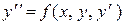 имеет бесконечное множество решений.
имеет бесконечное множество решений.
Пусть D – некоторая область изменения переменных х, у, у ¢, в которой выполнены условия теоремы Коши.
Определение 2.1 Общим решением дифференциального уравнения  в области D называется функция
в области D называется функция 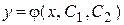 , зависящая от произвольных постоянных
, зависящая от произвольных постоянных 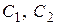 , непрерывно–дифференцируемая по переменной х и удовлетворяющая условиям:
, непрерывно–дифференцируемая по переменной х и удовлетворяющая условиям:
|
|
|
1) 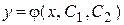 является решением этого дифференциального уравнения для любых значений
является решением этого дифференциального уравнения для любых значений 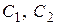 ;
;
2) для любых начальных условий 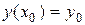 ,
, 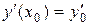 , где
, где  , существуют значения постоянных
, существуют значения постоянных 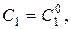
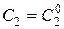 такие, что решение
такие, что решение 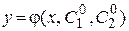 удовлетворяет этим начальным условиям.
удовлетворяет этим начальным условиям.
Общее решение, записанное в неявном виде 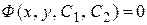 , называют общим интегралом дифференциального уравнения.
, называют общим интегралом дифференциального уравнения.
Определение 2.2 Частным решением дифференциального уравнения  называется функция
называется функция 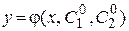 , полученная из общего решения
, полученная из общего решения 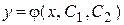 при конкретных значениях постоянных
при конкретных значениях постоянных 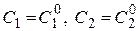 .
.
Заметим, что задача Коши, по существу, есть задача отыскания частного решения, удовлетворяющего заданным начальным условиям. Поэтому, чтобы найти частное решение дифференциального уравнения  , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям 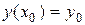 ,
, 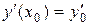 (решить задачу Коши), нужно использовать правило:
(решить задачу Коши), нужно использовать правило:
1. Найти общее решение 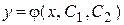 заданного дифференциального уравнения.
заданного дифференциального уравнения.
2. Найти производную  функции
функции 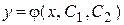 по переменной х.
по переменной х.
3. В равенствах 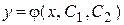 и
и  заменить х на х 0, у на у 0,
заменить х на х 0, у на у 0, 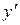 на
на 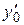 ; получится алгебраическая система уравнений
; получится алгебраическая система уравнений 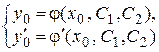 относительно
относительно 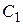 и
и  .
.
4. Решить эту систему уравнений и найти значения 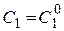 ,
,  .
.
5. Подставить найденные значения 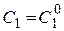 ,
,  в общее решение
в общее решение 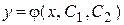 вместо постоянных
вместо постоянных 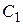 и
и  .
.
6. Полученная функция 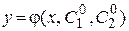 и есть искомое частное решение.
и есть искомое частное решение.
Как отмечалось выше, общее решение дифференциального уравнения определяет на плоскости О ху семейство интегральных кривых, что является его геометрической интерпретацией. Всякое частное решение определяет одну интегральную кривую этого семейства.
Выясним геометрический смысл задачи Коши нахождения решения  дифференциального уравнения
дифференциального уравнения  , удовлетворяющего начальным условиям
, удовлетворяющего начальным условиям
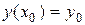 ,
, 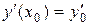 .
.
Условие 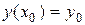 означает, что из семейства интегральных кривых уравнения выбирается кривая, проходящая через точку (х 0, у 0). Условие
означает, что из семейства интегральных кривых уравнения выбирается кривая, проходящая через точку (х 0, у 0). Условие 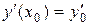 означает, что из всех интегральных кривых, проходящих через точку (х 0, у 0), выбирается та, тангенс угла наклона касательной к которой в этой точке равен у ¢0.
означает, что из всех интегральных кривых, проходящих через точку (х 0, у 0), выбирается та, тангенс угла наклона касательной к которой в этой точке равен у ¢0.
|
|
|
Таким образом, с геометрической точки зрения, задача Коши для дифференциального уравнения второго порядка означает отыскание интегральной кривой, проходящей через данную точку под заданным углом наклона*).
Рассмотрим механическую интерпретацию дифференциального уравнения второго порядка и его решения. Пусть материальная точка массы т движется по прямой (которую примем за ось О у) под действием силы F. Тогда у = у (t) – закон движения точки, 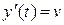 – скорость точки,
– скорость точки,  – ускорение. Согласно второму закону Ньютона имеем та = F, откуда
– ускорение. Согласно второму закону Ньютона имеем та = F, откуда 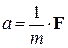 . Пусть сила F, действующая на точку, зависит от времени t, положения y точки на оси и скорости
. Пусть сила F, действующая на точку, зависит от времени t, положения y точки на оси и скорости 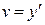 движения, т.е.
движения, т.е. 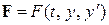 . Тогда
. Тогда  , или
, или
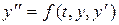 ,
,
где  . Таким образом, получили дифференциальное уравнение второго порядка.
. Таким образом, получили дифференциальное уравнение второго порядка.
Следовательно, дифференциальное уравнение второго порядка есть дифференциальное уравнение движения точки по прямой под действием силы, зависящей от времени, положения и скорости точки, а каждое его решение  определяет закон (уравнение) такого движения. Поэтому решение
определяет закон (уравнение) такого движения. Поэтому решение  дифференциального уравнения часто называют движением, определяемым уравнением
дифференциального уравнения часто называют движением, определяемым уравнением 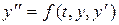 .
.
Задача Коши:
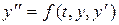 , у (t 0) = у 0, у ¢(t 0) = у ¢0.
, у (t 0) = у 0, у ¢(t 0) = у ¢0.
с механической точки зрения означает, что из всех движений, определяемых дифференциальным уравнением второго порядка, требуется выбрать то, для которого точка (двигаясь по оси Оу) в заданный момент времени t 0 займет положение у 0 и при этом будет иметь скорость у 0¢.
Рассмотрим методы интегрирования некоторых типов дифференциальных уравнений второго порядка.
I. Дифференциальные уравнения, допускающие понижение порядка.
Во многих случаях дифференциальное уравнение второго порядка
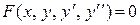
можно свести к уравнению первого порядка. Ниже в таблице перечислены некоторые виды дифференциальных уравнений, допускающих понижение порядка, и методы их интегрирования.
| Особенности и вид дифференциального уравнения | Метод интегрирования |
I. Уравнение не содержит 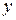 и и 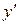 , т.е. имеет вид , т.е. имеет вид
 или
или
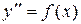
| Учитывая, что 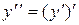 , заданное уравнение записать в виде , заданное уравнение записать в виде
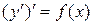 .
Два раза последовательно проинтегрировать: .
Два раза последовательно проинтегрировать:
 , ,
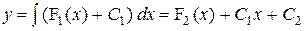 .
Искомое общее решение .
Искомое общее решение  . .
|
II. Уравнение не содержит явно неизвестной у, т.е. имеет вид
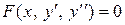
| 1) Сделать замену 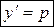 , , 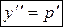 , где , где 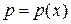 , ,  . Получится дифференциальное уравнение первого порядка относительно новой неизвестной функции р (х): . Получится дифференциальное уравнение первого порядка относительно новой неизвестной функции р (х):
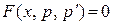 .
2) Определить тип этого уравнения и найти его общее решение .
2) Определить тип этого уравнения и найти его общее решение  (или общий интеграл (или общий интеграл 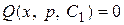 ).
3) В равенстве ).
3) В равенстве  (или (или 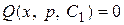 соответственно) заменить р на соответственно) заменить р на 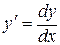 . Получится . Получится
|
еще одно дифференциальное уравнение первого порядка 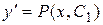 (или (или 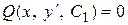 ).
4) Определить тип этого уравнения и найти его общее решение: ).
4) Определить тип этого уравнения и найти его общее решение: 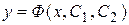 . .
| |
III.Уравнение не содержит явно независимой переменной х, т.е. имеет вид
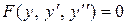 . .
| 1) Сделать замену 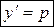 , ,  , где , где 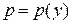 , ,  . Получится дифференциальное уравнение первого порядка относительно новой неизвестной функции р (у), т.е. . Получится дифференциальное уравнение первого порядка относительно новой неизвестной функции р (у), т.е.
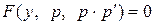 .
2) Определить тип этого уравнения и найти его общее решение .
2) Определить тип этого уравнения и найти его общее решение  (или общий интеграл (или общий интеграл 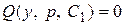 ).
3) В равенстве ).
3) В равенстве  (или (или 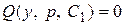 соответственно) заменить р на соответственно) заменить р на 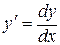 . Вновь получится еще дифференциальное уравнение первого порядка . Вновь получится еще дифференциальное уравнение первого порядка  (или (или 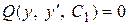 ).
4) Определить тип этого уравнения и найти его общее решение: ).
4) Определить тип этого уравнения и найти его общее решение: 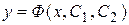 . .
|
Рассмотрим примеры решения таких уравнений.
|
|
|
Пример 2.1 Решить уравнение 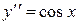 .
.
Решение
Поскольку в записи уравнения отсутствуют 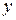 и
и 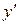 , то заданное уравнение является уравнением вида I (таблица 2). Следуя методу интегрирования таких уравнений, запишем уравнение в виде
, то заданное уравнение является уравнением вида I (таблица 2). Следуя методу интегрирования таких уравнений, запишем уравнение в виде 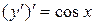 , откуда последовательно получаем
, откуда последовательно получаем
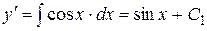 ,
,
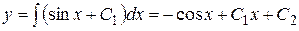 .
.
Итак, общее решение заданного уравнения 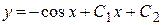 .
.
Ответ: 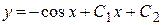 .
.
Пример 2.2 Решить дифференциальное уравнение 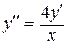 .
.
Решение
Заметим, что решение этого дифференциального уравнения следует искать при 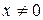 .
.
Данное уравнение не содержит переменной у, и, следовательно, является уравнением вида II (таблица 2).
Применим подстановку 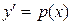 , тогда
, тогда  , где
, где  , и исходное уравнение примет вид
, и исходное уравнение примет вид
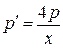 , или
, или  .
.
Получили дифференциальное уравнение первого порядка. Нетрудно убедиться в том, что это уравнение с разделяющимися переменными.
«Разделяя» переменные (при условии 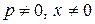 ), получим
), получим  , откуда имеем
, откуда имеем
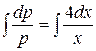 Þ
Þ 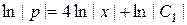 , или
, или 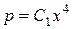 .
.
Учитывая, что  , получим новое дифференциальное уравнение первого порядка
, получим новое дифференциальное уравнение первого порядка 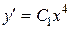 . Решим его:
. Решим его:
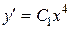 Þ
Þ 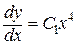 Þ
Þ 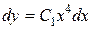 Þ
Þ 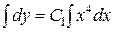 Þ
Þ
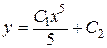 .
.
Итак, получили общее решение заданного дифференциального уравнения
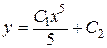 .
.
Ответ: 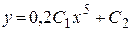 .
.
Пример 2.3 Найти решение дифференциального уравнения
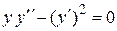 .
.
Решение
Поскольку данное уравнение не содержит независимой переменной х, то это – дифференциальное уравнение вида III (таблица 2). Сделаем замену
|
|
|
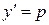 , где
, где 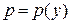 , тогда
, тогда 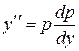 .
.
Подставляя в исходное уравнение, получим
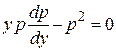
– дифференциальное уравнение первого порядка. Чтобы определить тип уравнения, запишем его в нормальной форме:
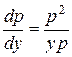 (
( ),
), 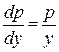 .
.
Очевидно, полученное уравнение есть дифференциальное уравнение с разделяющимися переменными. «Разделим» переменные и проинтегрируем уравнение:
 Þ
Þ  Þ
Þ 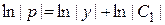 Þ
Þ
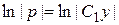 Þ р = С 1 у.
Þ р = С 1 у.
Учитывая, что 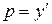 имеем ещё одно дифференциальное уравнение первого порядка
имеем ещё одно дифференциальное уравнение первого порядка

Решим его:
 Þ
Þ 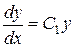 Þ
Þ  Þ
Þ 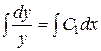 Þ
Þ
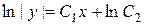 Þ
Þ 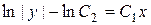 Þ
Þ 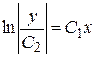 Þ
Þ
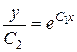 .
.
Отсюда 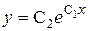 – общее решение исходного дифференциального уравнения.
– общее решение исходного дифференциального уравнения.
Проведем анализ решения. Поскольку на первом этапе интегрирования заданного дифференциального уравнения нам пришлось разделить на 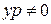 , нужно проверить, не потеряны ли решения этого уравнения.
, нужно проверить, не потеряны ли решения этого уравнения.
Пусть 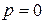 , т.е.
, т.е.  , тогда у = С. Эта функция является решением заданного дифференциального уравнения, поскольку удовлетворяет уравнению. Действительно:
, тогда у = С. Эта функция является решением заданного дифференциального уравнения, поскольку удовлетворяет уравнению. Действительно:
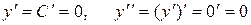 ,
,  – верное равенство.
– верное равенство.
И это решение не потеряно, т.к. функция 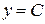 входит в семейство решений заданного дифференциального уравнения, описываемого формулой
входит в семейство решений заданного дифференциального уравнения, описываемого формулой 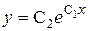 , при С 1 = 0, С 2 = С.
, при С 1 = 0, С 2 = С.
Функция 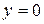 также есть решение исходного дифференциального уравнения:
также есть решение исходного дифференциального уравнения: 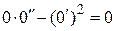 , но и она получается из общего решения
, но и она получается из общего решения 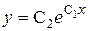 при
при 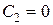 , и поэтому не является потерянным решением. Таким образом, формула
, и поэтому не является потерянным решением. Таким образом, формула  описывает все возможные решения данного дифференциального уравнения.
описывает все возможные решения данного дифференциального уравнения.
Ответ:  .
.
Замечание
При решении задачи Коши для дифференциального уравнения, допускающего понижение порядка, целесообразнее определять значения постоянных С 1 и С 2 в процессе решения, а не после того как будет найдено общее решение. Это ускоряет ход решения задачи, а в некоторых случаях значительно упрощает дальнейшее интегрирование.
Рассмотрим пример.
Пример 2.4 Найти решение дифференциального уравнения
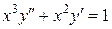 ,
,
удовлетворяющее условиям  ,
, 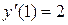 .
.
Решение
Данное дифференциальное уравнение не содержит переменной у и следовательно, является дифференциальным уравнением, допускающим понижение порядка типа II (таблица 2). Сделаем замену
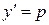 , где
, где 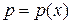 , тогда
, тогда  .
.
Получим дифференциальное уравнение первого порядка
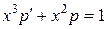 .
.
Разделим обе части этого уравнения на 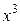 (считая
(считая 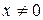 ), получим
), получим
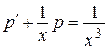
– линейное дифференциальное уравнение первого порядка. Будем решать его методом Бернулли (таблица 1). Положим 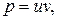 где
где 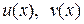 – новые неизвестные функции. Тогда
– новые неизвестные функции. Тогда 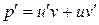 и уравнение примет вид
и уравнение примет вид
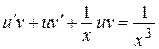 , или
, или 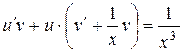 ,
,
а функции 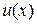 и
и  найдём из системы уравнений
найдём из системы уравнений 
1) Функцию v находим из уравнения 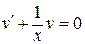 . Имеем:
. Имеем:
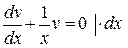 Þ
Þ 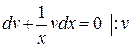 Þ
Þ  Þ
Þ 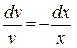 .
.
Отсюда
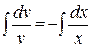 Þ
Þ 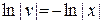 *) Þ
*) Þ 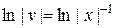 Þ
Þ  .
.
2) При  найдем функцию и из уравнения
найдем функцию и из уравнения 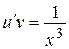 :
:
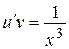 Þ
Þ 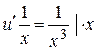 Þ
Þ  Þ
Þ 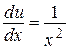 Þ
Þ
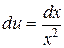 Þ
Þ 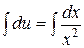 Þ
Þ  .
.
|
|
|
Следовательно, 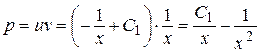 .
.
Учитывая, что 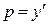 , получим еще одно дифференциальное уравнение первого порядка:
, получим еще одно дифференциальное уравнение первого порядка:
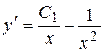 .
.
Так как по условию 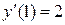 , то получаем
, то получаем
 , откуда
, откуда 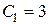 .
.
Таким образом, для отыскания неизвестной функции у имеем дифференциальное уравнение первого порядка
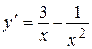 , или
, или 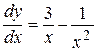 , откуда
, откуда 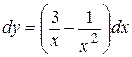 .
.
Интегрируя, находим
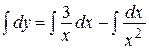 ,
,  .
.
Учитывая начальное условие у (1) = 1, получаем
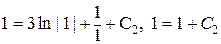 ,
, 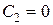 ,
,
значит, искомое частное решение имеет вид 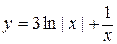 .
.
Ответ: 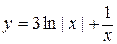 .
.
2. Общая теория линейных дифференциальных уравнений второго порядка
Многие задачи математики, механики, электротехники и других технических наук приводят к линейным дифференциальным уравнениям различных порядков, поэтому теория их интегрирования является наиболее разработанной частью теории дифференциальных уравнений. Ранее мы рассматривали решение линейных дифференциальных уравнений первого порядка. Теперь рассмотрим линейные дифференциальные уравнения любого, в частности, второго порядка.
Определение 3.1 Дифференциальное уравнение п -го порядка, линейное относительно неизвестной функции и всех ее производных, входящих в это уравнение, называется линейным дифференциальным уравнением п -го порядка.
В общем виде линейное дифференциальное уравнение п- го порядка записывают так
 , (3.1)
, (3.1)
где 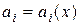 ,
,  – заданные функции от х или постоянные, причем
– заданные функции от х или постоянные, причем 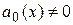 для всех значений х из той области, в которой рассматривается уравнение (3.1).
для всех значений х из той области, в которой рассматривается уравнение (3.1).
Если  , то уравнение (3.1) называется линейным однородным дифференциальным уравнением или уравнением без правой части:
, то уравнение (3.1) называется линейным однородным дифференциальным уравнением или уравнением без правой части:
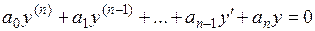 . (3.2)
. (3.2)
Если 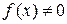 на
на 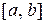 , то уравнение (3.1) называют линейным неоднородным дифференциальным уравнением п -го порядка или уравнением с правой частью. Функция
, то уравнение (3.1) называют линейным неоднородным дифференциальным уравнением п -го порядка или уравнением с правой частью. Функция  при этом называется правой частью линейного неоднородного дифференциального уравнения. Уравнение (3.2) называется линейным однородным дифференциальным уравнением, соответствующим линейному неоднородному дифференциальному уравнению (3.1).
при этом называется правой частью линейного неоднородного дифференциального уравнения. Уравнение (3.2) называется линейным однородным дифференциальным уравнением, соответствующим линейному неоднородному дифференциальному уравнению (3.1).
Теорию интегрирования линейных дифференциальных уравнений рассмотрим на примере уравнений второго порядка. Линейное однородное дифференциальное уравнение второго порядка имеет вид
 ,
,
а неоднородное –
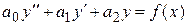 .
.
Сформулируем теорему существования и единственности решения линейного дифференциального уравнения.
Теорема 3.1
Если функции 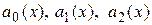 и
и  непрерывны на отрезке
непрерывны на отрезке 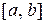 , то для любого
, то для любого  и произвольных чисел
и произвольных чисел 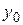 ,
, 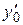 существует единственное решение
существует единственное решение 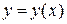 уравнения
уравнения 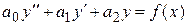 , удовлетворяющее условиям
, удовлетворяющее условиям  ,
, 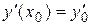 .
.
В дальнейшем, чтобы обеспечить существование решения линейного дифференциального уравнения, будем предполагать, что коэффициенты 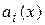 и правая часть
и правая часть  этого уравнения есть непрерывные на некотором интервале
этого уравнения есть непрерывные на некотором интервале 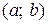 функции.
функции.
Рассмотрим линейное однородное дифференциальное уравнение
 . (3.3)
. (3.3)
При выполнении условий теоремы 3.1 уравнение имеет бесконечное множество решений, которые обладают следующим свойством:
 Если
Если 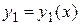 и
и 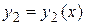 – решения линейного однородного дифференциального уравнения (3.3), то для любых значений постоянных С 1, С 2 функция
– решения линейного однородного дифференциального уравнения (3.3), то для любых значений постоянных С 1, С 2 функция 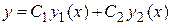 также есть решение этого уравнения.
также есть решение этого уравнения.
Решим вопрос нахождения общего решения уравнения (3.3). Для этого введем понятие линейной независимости (линейной зависимости) решений линейного однородного дифференциального уравнения.
Определение 3.1 Решения 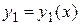 и
и 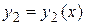 называются линейно независимыми на интервале
называются линейно независимыми на интервале 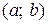 , если для любого
, если для любого 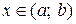 их отношение не является постоянной величиной:
их отношение не является постоянной величиной:
 (
(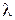 – const).
– const).
Решения 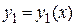 и
и  называются линейно зависимыми на интервале
называются линейно зависимыми на интервале 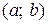 , если для любого
, если для любого 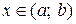 их отношение постоянно:
их отношение постоянно:  (
(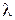 – const).
– const).
Определение 3.2 Фундаментальной системой решений (ФСР) линейного однородного дифференциального уравнения второго порядка называется совокупность любых двух линейно независимых на интервале 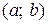 частных решений этого уравнения.
частных решений этого уравнения.
Вопрос о нахождении общего решения линейного однородного дифференциального уравнения решает следующая теорема.
Теорема 3.2 (о структуре общего решения линейного однородного дифференциального уравнения)
Общим решением линейного однородного дифференциального уравнения (3.3) является функция
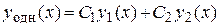 ,
,
где { 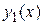 ,
, 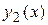 } – какая-либо фундаментальная система решений этого дифференциального уравнения, а С 1, С 2 – произвольные постоянные.
} – какая-либо фундаментальная система решений этого дифференциального уравнения, а С 1, С 2 – произвольные постоянные.
Таким образом, чтобы найти общее решение однородного линейного дифференциального уравнения следует воспользоваться алгоритмом:
1. Отыскать какую-либо фундаментальную систему { 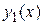 ,
, 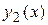 } решений уравнения.
} решений уравнения.
2. Записать функцию 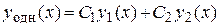 , которая и является общим решением уравнения.
, которая и является общим решением уравнения.
Рассмотрим теперь неоднородное линейное дифференциальное уравнение второго порядка
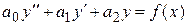 . (3.4)
. (3.4)
Оказывается, если известно какое-либо частное решение уравнения (3.4), то нахождение его общего решения сводится к нахождению общего решения соответствующего однородного линейного уравнения (3.3).
Теорема 3.3 (о структуре общего решения линейного неоднородного дифференциального уравнения)
Общее решение  линейного неоднородного дифференциального уравнения
линейного неоднородного дифференциального уравнения 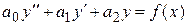 равно сумме общего решения
равно сумме общего решения 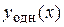 линейного однородного дифференциального уравнения, соответствующего данному, и
линейного однородного дифференциального уравнения, соответствующего данному, и
какого-либо частного решения 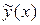 заданного неоднородного дифференциального уравнения:
заданного неоднородного дифференциального уравнения:
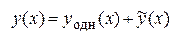 .
.
Таким образом, чтобы найти общее решение линейного неоднородного дифференциального уравнения можно использовать следующий алгоритм:
1. Найти общее решение 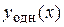 соответствующего однородного уравнения.
соответствующего однородного уравнения.
2. Найти какое-либо частное решение 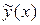 исходного уравнения.
исходного уравнения.
3. Записать функцию 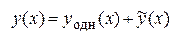 .
.
Практическую реализацию сформулированных алгоритмов рассмотрим для линейных дифференциальных уравнений второго порядка с постоянными коэффициентами.
*) Под углом наклона кривой понимают угол, который образует её касательная с положительным направлением оси О х.
*) Согласно методу Бернулли, находим частное решение этого дифференциального уравнения, поэтому сразу возьмём постоянную С равной нулю.
|
|
|


