Слушатель: 4. Слушатели: 6. А.С.: Без сомнения. А граней?

Слушатель: 4.

А. С.: В = 4. Сколько ребер у нашего тетраэдра?

 

Слушатели: 6.

А. С.: Без сомнения. А граней?

 

Слушатели: 4.

А. С.: Верна формула? 4 – 6 + 4 = 2. Верна.

А теперь рассмотрю другую пирамиду – четырехугольную (рис. 27).

 

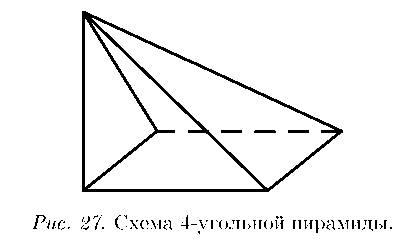
У нее 5 вершин, 8 ребер и 5 граней. Формула верна: 5^8 + 5 = 2. Слушатель: А количество вершин и граней всегда совпадает? А. С.: Нет, ни в коем случае не всегда. Давайте посмотрим на куб (рис. 26, слева).

У обычного куба – 8 вершин, 12 ребер и 6 граней. (Бывают еще и необычные кубы... например, 4‑ мерные. )

Снова получаем два: 8 – 12 + 6 = 2.

Никуда от этой формулы не денешься. Думаю, что до Эйлера эту закономерность тоже кто‑ то замечал, но важно не первым за­метить, а громко об этом заявить. Так сказать, довести до сведения широких масс.

Не буду сегодня ничего больше доказывать. Вместо этого я рас­скажу о некоторых великих математических загадках прошлого.

Давайте вспомним формулу для решения квадратного уравне­ния с коэффициентами а, Ь, с:

_ ± %/fo² – 4ас ^Ж_ 2а '

На самом деле не очень важно, как конкретно она выглядит. Важно то, что это – универсальный метод решения квадратного уравне­ния. Какие бы они ни были, эти а, Ъ и с, если действие произвести, вы получите какое‑ то число.

Тут есть две точки зрения на эту ситуацию. Если написа­на некоторая формула, то она может случайно оказаться верной для каких‑ то чисел а, Ь, с, то есть для какого‑ то квадратного трех­члена. Для одного случайно оказалась верной, для другого ока­залась верной. Сколько раз нужно проверять, чтобы точно ска­зать, что она всегда верна? Бесконечное количество раз. Но можно сделать иначе. Можно взять эту формулу, подставить в исходное уравнение

ах ² + Ьх + с = О

и убедиться в том, что всё сократится, и вместо символов а, Ь, с слева возникнет ноль. Это и будет означать, если мы верим в язык символов, что формула верна. У нас всё сократилось, в любом случае, какие бы а, Ь, с мы ни взяли.

Слушатель: Простите, а для чего нужна эта формула?

А. С.: Для чего она нужна? Ну, я бы сказал так. Лично для ме­ня ответ такой: для красоты. Для того, чтобы быть уверенным, что математика может дать какие‑ то универсальные рецепты вычисле­ний. Сейчас, конечно, компьютеры решают задачи посложнее этого уравнения, но раньше она была нужна для быстрого вычисления.

Вы распределяете земельные участки, измеряете какие‑ то пря­моугольные куски, у вас получается квадратное уравнение. Можно медленно прикидывать, как это сделать, а можно быстро получить ответ.

Слушатель: То есть практическое применение какое‑ то было?

А. С.: Ну, раньше – да. Дальше эта идея развивалась так. А что, если я напишу уравнение:

аж³ + Ьх ² + сх + d = О?

Могу я написать универсальную формулу, с помощью которой можно вычислить ж? При этом разрешается складывать, вычитать, умножать, делить и даже извлекать корни, причем любой степени. Но больше ничего не разрешается.

Слушатель: От куба и дальше такого сделать нельзя.

А. С.: Можно; но эту формулу не изучают в школе. Форму­ла для кубического случая была придумана в первой половине XVI века. Несколько математиков работали над этой проблемой одновременно. Сейчас формула носит имя Джироламо Кардано, но он не придумал ее, а опубликовал метод другого математика (т. е. «громко об этом заявил»).

Чтобы выписать эту формулу, мне понадобится целая доска, поэтому я не буду этого делать. Как только поняли механизм ре­шения кубического уравнения, сразу придумали формулу для ре­шения уравнения четвертой степени. Она была еще страшнее. Вы­вел ее ученик Кардано, по фамилии Феррари. Всё это происходило в XVI веке, когда математики уже свободно обращались с буква­ми, поэтому был сформулирован самый общий вопрос. Можно ли написать формулу для решения уравнения произвольной степени:

а _п х ^п  + a _n ‑ ix ⁿ+... + a, Q = О

(а _п, а _п ‑ 1,... – известные числа. Так обозначают для удобства. А то вдруг не хватит букв алфавита для их обозначения? )?

Пусть она займет 10 досок, пусть она займет 100 досок. Пого­ня за этой формулой продолжалась до конца XVIII века. А в са­мом начале XIX века прозрение спустилось на несколько человек сразу, из которых самым главным я считаю французского мате­матика Эвариста Галуа (хотя первым ситуацию в общих чертах осознал Жозеф Луи Лагранж). Было доказано, что никакая ко­нечная формула не может быть решением уравнения произволь­ной степени. Такой формулы не существует. Не потому, что люди еще глупые или не все формулы перебрали или, может быть, они не так ставили корни. Никакое выражение, содержащее плюс, ми­нус, умножить, разделить и извлечь корень любой степени не мо­жет при подстановке в уравнение а _п х ^п  + а„_\х ^п ^ ¹  +... + ао = О полностью сократиться. Это – математически строгий результат начала XIX века7.

Еще очень известна теорема Ферма. Доказательство теоремы Ферма – это примерно 120 страниц трудного текста для очень посвященного человека.

Про нее мы поговорим потом, а сейчас просто запишем ее фор­мулировку. Она очень простая.

Ни для каких целых чисел ж, у, г, отличных от нуля, и никакого натурального п, большего 2, не может выполняться равенство:

 

х^п + у^п = zⁿ.

Эту теорему доказывали с 1637 по 1994 год. Впоследствии были решены еще две или три величайшие математические проблемы прошлых веков. Сейчас математика пожинает плоды всего своего существования.

Слушатель: Это сделано с помощью компьютеров?

А. С.: Нет. Единственное, что сделали с помощью компьюте­ра – это так называемая «проблема четырех красок». XX век – прорыв в авиации, в космосе. Но самый большой прорыв в это вре­мя был в математике. В ней перевернули всё вверх дном: сняли кучу гипотез, превратили их в теоремы. На моей памяти сняли не­сколько проблем, которые стояли веками, если не тысячелетиями.

Слушатель: А это правда, что у теоремы Ферма нет практи­ческого применения?

А. С.: А кто его знает? Она (точнее, метод ее доказательства) может иметь некоторое отношение к физической модели мира. На самом деле, последнее, что интересно математику, это то, ка­кое у теоремы практическое применение. Математика в каком‑ то смысле сродни настоящей религии. Это вещь в себе. Если она кому‑ то помогает, математиков это особо не интересует. Люди, которые занимаются прикладной математикой, имеют совершенно другое настроение. Это – другие люди. Как, например, разнятся между собой учителя и чиновники. То же самое с математиками. Чело­век, который формулу ищет, и человек, который хочет с помощью нее что‑ то сделать, – это два разных человека.

На этом мы закончим первую лекцию. На следующем занятии мы будем доказывать теорему про футбольный мяч и формулу Эйлера.

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: