Главная | Обратная связь | Поможем написать вашу работу!

Внетабличное умножение и деление в пределах 100

К внетабличным случаям умножения и деления в пределах 100 относят случаи умножения двузначного числа на однозначное (20-3, 18-3),а также случаи деления двузначного числа на однозначное, не входящие в число табличных (80: 4, 96: 6) и случаи деления двузначного числа на двузначное в пределах 100 (80: 40, 96: 16). Эти случаи рассматриваются как случаи устных вычислений, и предполагается, что ребенок выполняет их без обращения к письменным алгоритмам вычислений, а лишь используя известные ему правила и законы арифметических действий и знание табличного умножения и деления.

Используемые математические законы и правила

Для подготовки к изучению внетабличного умножения и деления необходимо рассмотреть следующие правила арифметических действий:

1) правило умножения суммы на число и правило умножения числа на сумму;

2) правило деления суммы на число;

3) правило группировки множителей (сочетательное свойство умножения).

Рассмотрим каждое из этих правил и обоснуем их использование при устных внетабличных вычислениях.

Правило умножения суммы на число и правило умножения числа на сумму

Эти два правила являются двумя вариантами раскрытия смысла распределительного свойства умножения относительно сложения. В буквенном виде эти варианты могут быть записаны следующим образом:

(a+b) •c=a•c+b•c с•(a+b)=с•a+с•b

Реально знакомство детей с этими двумя вариантами одного и того же правила разведено во времени почти на целый год: первое правило лежит в основе обучения детей умножению двузначных чисел на однозначные в теме «Внетабличное умножение и деление» в 3 классе, а второе правило лежит в основе способа действия при умножении двузначного числа на двузначное при умножении в столбик в 4 классе.

В основе разъяснения правила умножения суммы на число лежит опора на знание конкретного смысла действия умножения.

Рассматривая два способа вычисления результатов с опорой на анализ рисунка, дети убеждаются в том, что результат при обоих способах вычислений одинаков.

Следует отметить, что первый способ вычислений не требует специальных объяснений и введения нового правила, поскольку он подчиняется общим требованиям к порядку выполнения действий в выражениях со скобками: действия в скобках выполняются первыми.

Особо следует оговорить второй способ, поскольку при таких вычислениях фактически нарушается установка на выполнение действия в скобках первым. Именно поэтому при знакомстве детей с этим правилом в 3 классе снова возвращаются к предметным картинкам, позволяющим получить результаты действий пересчетом. В данном случае пересчет фигурок является тем единственным аргументом, который учитель может привести в подкрепление правомочности такого нарушения устоявшегося правила (действие в скобках выполняется первым).

Введение правила таким образом является нестрогим, эмпирическим (т. е. опирающимся на непосредственный практический опыт). Более общие способы доказательства этого закона требуют привлечения сложного математического аппарата и нецелесообразны в начальной школе. Безусловно, такое введение правила не формирует у детей обобщенных представлений о способах раскрытия скобок при вычислениях, однако в начальной школе это и не предполагается. Более того, терминология, содержащая слова «раскрываем скобки», не употребляется в начальной школе вообще. Хотя дети и знакомятся с правилом умножения суммы на число, но применять они его могут только на ограниченном количестве случаев, связанных с внетабличным умножением двузначных чисел на однозначное. Применение того же правила в других обстоятельствах (например, при решении уравнений) не предусмотрено. Так при решении уравнения вида (х + 2) • 3 = 15 дети не будут применять правило умножения суммы на число (это не предусмотрено ни учебником, ни программой, ни методикой) не только в начальной школе, но и в 5—6 классе, а будут использовать правила взаимосвязи компонентов действий умножения и сложения.

Способ решения: х + 2 = 15: 3 х+2 = 5х = 5 — 2 х = 3.

Правило умножения суммы на число:

Чтобы умножить сумму на число, можно умножить на это число каждое слагаемое и полученные результаты сложить.

Используя аналогичный предметный рисунок, рассматривают правило умножения числа на сумму:

4-(3 + 2) = 4- 5 = 20 4-(3 + 2) = 4-3 + 4- 2 = 12 + 8 = 20

Анализ предметного рисунка и подсчет фигурок на нем помогает ребенку убедиться в том, что результаты вычислений совпадают, несмотря на разные способы вычислений. Этот способ знакомства с правилом используется в 4 классе также как и в 3 классе использовался предыдущий вариант. Точно также, речь идет не о формировании у ребенка обобщенных представлений о способах действий в выражениях со скобками, а только об использовании данного способа вычислений при письменных вычислениях в столбик.

Правило умножения числа на сумму:

Чтобы умножить число на сумму можно умножить это число на каждое слагаемое и полученные произведения сложить.

Правило деления суммы на число

Это правило является вариантом раскрытия смысла распределительного свойства деления относительно сложения. В буквенном виде это правило может быть записано следующим образом:

(a + b): с = a: с + b: с

В основе разъяснения правила деления суммы на число лежит опора на знание конкретного смысла действия деления. Например:

(8 + 6): 2 = 14:2 = 7 (8 + 6): 2 = 8: 2+ 6: 2 = 4+ 3 = 7

Такое введение правила является нестрогим, эмпирическим. Более общие способы доказательства этого закона требуют привлечения сложного математического аппарата и нецелесообразны в начальной школе. Такое введение правила не формирует у детей обобщенных представлений о способах раскрытия скобок при вычислениях, что в начальной школе и не предполагается. Хотя дети и знакомятся с правилом деления суммы на число, но применять они его могут только на ограниченном количестве случаев, связанных с внетабличным делением двузначных чисел на однозначные. Применение того же правила в других обстоятельствах (например, при решении уравнений) не предусмотрено. Так при решении уравнения вида (х + 6): 3 = 5 дети не будут применять правило деления суммы на число (это не предусмотрено ни учебником, ни программой, ни методикой) не только в начальной школе, но и в 5—6 классе, а будут использовать правила взаимосвязи компонентов действий умножения и сложения.

Способ решения: х + 6 = 5 • 3 д: + 6=15 х=15-6 х = 9

Правило деления суммы на число:

Чтобы разделить сумму на число, можно разделить на это число каждое слагаемое и полученные результаты сложить.

Правило группировки множителей (сочетательное свойство умножения)

Правило группировки множителей (сочетательное свойство умножения) представлено в учебнике как правило умножения числа на произведение. Это правило позволяет научить детей новым способам действия при выполнении устных внетабличных вычислений. В буквенном виде правило может быть представлено следующим образом:

(а • b) • с = а • (b • с) ~ (а • с) • b

В основе его разъяснения лежит конкретный смысл действия умножения и правило перестановки множителей.

Рассматривая три способа вычисления результатов с опорой на анализ рисунка, дети убеждаются в том, что результат при всех способах вычислений одинаковый. Формулируется правило:

Умножить число на произведение можно разными способами:

1) Вычислить произведение и умножить на него число: 6-(3-4) =612 = 72

2) Умножить число на первый множитель и результат умножить на второй множитель:

6 (3 4) = (6 3) 4= 18 4 = 72

3) Умножить число на второй множитель и результат умножить на первый множитель:

6 (3 4) - (6 4) 3=24 3 = 72 Фактически все три данные правила могут быть заменены более короткой общей формулировкой:

Произведение двух соседних множителей можно заменить его значением.

Или:

Чтобы найти произведение нескольких множителей, их можно перемножить в любом порядке.

Методически данное правило имеет целью подготовить ребенка к знакомству со способами умножения в столбик чисел, оканчивающихся нулями, поэтому с ним знакомятся только в четвертом классе. Реально данное свойство умножения позволяет рационализировать устные вычисления как во 2, так и в 3 классе.

Например:

Вычисли:

(7 • 2) • 5 =...

В данном случае намного легче вычислить вариант 7-(2 5) = 7 10 = 70.

Вычисли:

12 • (5 • 7) =...

В данном случае намного легче вычислить вариант (12-5)-7 = 60-7 = 420.

Приемы вычислений

1. Умножение и деление чисел, оканчивающихся нулем:

20-3; 3 • 20; 60: 3; 80: 20

Вычислительный прием в данном случае сводится к умножению и делению однозначных чисел, выражающих число десятков в заданных числах.

Например:

20.3=... 3-20 =... 60:3 =...

2 дес. -3= 20-3 = 60 6 дес.: 3 = 2 дес.

20-3 = 60 3-20 = 60 60:3 = 20

Для случая 80:20 может быть использовано два способа вычислений: тот, что использовался в предыдущих случаях, и способ подбора частного.

Например:

80: 20 =... 80: 20 =...

8 дес.: 2 дес. = 4 или 20 • 4 = 80

80:20 = 4 80:20 = 4

В первом случае использовался прием представления двузначных десятков в виде разрядных единиц, что сводит рассматриваемый случай к табличному (8:2). Во втором случае цифра частного находится подбором и проверяется умножением. Во втором случае ребенок возможно не сразу подберет верную цифру частного, это означает, что проверка будет выполнена не один раз.

2. Прием умножения двузначного числа на однозначное: 23 • 4; 4-23

При умножении двузначного числа на однозначное актуализируются следующие знания и умения:

23-4 = (20 + 3).4 - 20-4 + 3-4 = 80 + 12 = 92 разрядный свойство умножения сложение состав числа суммы на число двузначных

S \ чисел

20-4 + 34 умножение таблица целых умножения десятков

В случае умножения вида 4 • 23 сначала применяется перестановка множителей, а затем та же схема умножения, что и выше.

3. Прием деления двузначного числа на однозначное: 48:3; 48:2

При делении двузначного числа на однозначное актуализируются следующие знания и умения:

48:3 = (30+ 18):3 = 3d:3 + 18:3 = 10 + 6=16 «удобные» свойство деления «разрядное»

слагаемые суммы на число сложение

/ \ 30:3 18:3 деление табличное целых деление десятков

В случае 48: 2 = (40 + 8): 2, а дальше аналогично предыдущему случаю. разрядные

слагаемые

4. Прием деления двузначного числа на двузначное: 68:17

При делении двузначного числа на двузначное необходимы следующие знания и умения:

68:17 = *

Прием подбора частного Связь деления и умножения

2 • 17 = 17 * 2 = 34 < 68

коммутативность

умножения

3*17 = 17*3=5<68

умножение двузначного на однозначное

4 • 17 = 17 • 4 = 68

68: 17 = 4

Сложность последнего приема состоит в том, что ребенок не может сразу подобрать нужную цифру частного и выполняет несколько проверок подобранных цифр, что требует достаточно сложных вычислений. Многие дети тратят много времени на выполнение вычислений этого вида, поскольку начинают не столько подбирать подходящую цифру частного, сколько перебирают все множители подряд, начиная с двух.

С целью облегчения вычислений могут быть использованы два приема:

1) ориентировка на последнюю цифру делимого;

2) прием округления.

Первый прием предполагает, что при подборе возможной цифры частного ребенок ориентируется на знание таблицы умножения, сразу перемножая подобранную цифру (число) и последнюю цифру делителя.

Например, 3-7 = 21. Последняя цифра числа 68 - это 8, значит нет смысла умножать 17 на 3, последняя цифра делителя все равно не совпадает. Пробуем в частном число 4 — умножаем 7 • 4 = 28. Последняя цифра совпадает, значит имеет смысл найти произведение 17 ■ 4.

Второй прием предполагает округление делителя и подбор цифры частного с ориентиром на округленный делитель.

Например, 68:17 делитель 17 округляется до 20. Примерная цифра частного 3 дает при проверке 20 • 3 = 60 < 68, значит имеет смысл сразу проверять в качестве цифры частного 4:17 • 4 = 68.

Эти приемы позволяют сократить затраты сил и времени при выполнении вычислений данного вида, но требуют хорошего знания таблицы умножения и умения округлять числа.

Целые числа, оканчивающиеся цифрами 0,1,2,3,4, округляют до ближайшего целого десятка, отбрасывая эти цифры.

Например, числа 12, 13, 14 следует округлять до 10. Числа 62, 63, 64 округляют до 60.

Целые числа, оканчивающиеся цифрами 5, 6, 7,8,9, округляют до ближайшего целого десятка в большую сторону.

Например, числа 15,16,17,18,19 округляют до 20. Числа 45,47, 49 округляют до 50.

Порядок действий в выражениях, содержащих умножение и деление

Правила порядка выполнения действий задают основные признаки выражений, на которые следует ориентироваться при вычислении их значений.

Первые правила, определяющие порядок действий в арифметических выражениях, задавали порядок действий в выражениях, содержащих действия сложения и вычитания:

1. В выражениях без скобок, содержащих только действия сложения и вычитания, действия выполняются в том порядке, как они записаны: слева направо.

2. Действия в скобках выполняют первыми.

3. Если выражение содержит только действия сложения, то два соседних слагаемых всегда можно заменить их суммой (сочетательное свойство сложения).

В 3 классе изучаются новые правила порядка выполнения действий в выражениях, содержащих умножение и деление:

4. В выражениях без скобок, содержащих только умножение и деление, действия выполняются в том порядке, как они записаны: слева направо.

5. В выражениях без скобок умножение и деление выполняются раньше, чем сложение и вычитание.

При этом установка на выполнение действия в скобках первым сохраняется. Возможные случаи нарушения этой установки были оговорены ранее.

Правила порядка выполнения действий являются общими правилами вычислений значений математических выражений (примеров), которые сохраняются на протяжении всего периода изучения математики в школе. В связи с этим формирование у ребенка четкого понимания алгоритма порядка выполнения действий является важной преемственной задачей обучения математике в начальной школе. Проблема заключается в том, что правила порядка выполнения действий являются достаточно вариативными и не всегда однозначно заданными.

Например, в выражении 48-3 + 7 + 8 следует по общей установке применять правило 1 для выражения без скобок, содержащего действия сложения и вычитания. В то же время, как вариант рациональных вычислений, можно использовать прием замены суммой части 7 + 8, поскольку после вычитания числа 3 из 48 получится 45, к чему удобно прибавить 15.

Однако подобный разбор такого выражения в начальных классах не предусмотрен, поскольку есть опасения, что при неадекватном понимании такого подхода ребенок будет применять его в случаях вида 72 - 9 - 3 + 6. В данном случае замена выражения 3 + 6 суммой невозможна, она приведет к неверному ответу.

Большая вариативность в применении всей группы правил и вариантов правил при определении порядка действий требует значительной гибкости мышления, хорошего понимания смысла математических действий, последовательности мыслительных действий, математического «чутья» и интуиции (математики называют это «чувство числа»). Реально намного проще приучить ребенка жестко соблюдать четко установленный порядок анализа числового выражения с точки зрения тех признаков, на которые ориентировано каждое правило.

Определяя порядок действий, рассуждай так:

1) Если есть скобки, выполняю первым действие, записанное в скобках.

2) Выполняю по порядку умножение и деление.

3) Выполняю по порядку сложение и вычитание.

Данный алгоритм задает порядок действий достаточно однозначно, хотя и с небольшими вариациями. Например:

2 1 2 1

100-21:3 = 100-7 = 93 60 + 9-3 = 60 + 27 = 87

3 2 1

30+6 • (13 - 9) = 30 + 6 • 4 = 30 + 24 = 54

В этих выражениях порядок действий определен алгоритмом однозначно и является единственно возможным. Приведем другие примеры:

3 14 2 5

54 16 • 3 - 72:81 6 = 54 + 18 - 72: 8 + 6 = 54 + 18 - 9 + 6 = 72 --9 + 6=63 + 6 = 69

После выполнения умножения и деления в данном примере можно было сразу к 54 прибавить 6, а из 18 вычесть 9, после чего результаты сложить. Технически было бы значительно легче, чем путь, обусловленный алгоритмом, возможен изначально другой порядок действий в примере:

3 2 4 1 5

54 + 6^3-72:8 + 6 — этот путь не противоречит алгоритму, хотя также не является рациональным.

Таким образом, вопрос о формировании умения определять порядок действий в выражениях в начальной школе определенным образом противоречит необходимости обучать ребенка способам рациональных вычислений.

Например, в случае порядок действий определен алгоритмом

абсолютно однозначно, при этом требует от ребенка сложнейших вычислений в уме с переходами через разряд: 42 - 7 и 35 + 8.

Если же после выполнения деления 21:3, выполнить сложение 42 + 8 = 50, а затем вычитание 50 - 7 = 43, что намного легче технически, ответ будет тот же. Этот путь вычислений противоречит установке данного в учебнике алгоритма, хотя и является рациональным.

В общем можно сказать, что изменять порядок действий, оговоренный правилом, можно только в тех случаях, когда это позволяют законы сложения и умножения (сочетательный и распределительный). Для того, чтобы научить ребенка распознавать такие случаи, необходимо реализовать при обучении математике специальную систему формирования рациональных вычислений. Одним из элементов этой системы является знакомство ребенка с признаками делимости чисел.

Признаки делимости

Признаки делимости как таковые не рассматриваются в начальной школе специально.. Единственным признаком делимости, рассматриваемым в новом учебнике математики можно считать понятие о четности натуральных чисел в учебнике 3 класса:

Числа, которые делятся на 2, называются четными, а числа, которые не делятся на 2, — нечетными.

Однако целью введения данного определения является не столько знакомство детей с одним из признаков делимости (являющимися крайне полезными с точки зрения формирования вычислительных умений и рациональных вычислений), что видно из формы построения определения, а знакомство детей с еще одним математическим термином (понятием), определенным по соглашению (методом сообщения ребенку термина и его значения).

Умение применять признаки делимости для рационализации вычислений является важным и полезным умением перспективного характера, сохраняющим свою ценность в старших классах.

Признак делимости на 2:

Если последняя цифра числа делится на 2, то и само число разделится на 2.

Например:

49 — последняя цифра 9 на 2 не делится, значит, и все число на 2 не разделится.

12 345 678 — последняя цифра 8 на 2 делится, значит, и все число на 2 разделится.

12 345 678: 2 = 6 172 839

Признак делимости на 3:

Если сумма цифр числа делится на 3, то и само число разделится на 3.

Например:

375 — сумма цифр 3 + 7 + 5= 15 делится на 3, значит, и само число разделится на 3. 375: 3 = 125.

679 — сумма цифр 6 + 7 + 9 = 22 не делится на 3, значит, и само число не разделится на 3.

Признак делимости на 4:

Если две последние цифры числа образуют число, делящееся на 4, то и само число разделится на 4.

Например:

3732 — две последние цифры образуют число 32, которое делится на 4, значит число 3732 разделится на 4. 3732: 4 = 933.

Число 3700 также разделится на 4, поскольку две последние цифры — это нули, а нуль делится на любое число. 3700: 4 = 925.

Признак делимости на 5:

Если число оканчивается на 0 или на 5, то оно делится на 5.

Например:

3700 — делится на 5,3705 — делится на 5, а 3703 — не делится на 5. Признак делимости на 9:

Если сумма цифр числа делится на9, то и само число разделится на 9.

Например:

7245 — сумма цифр 7 + 2 + 4 + 5 =18 делится на 9, значит и само число разделится на 9. 7245: 9 = 805.

7234 — сумма цифр 7 + 2 + 3 + 4 = 16 не делится на 9, значит и само число не разделится на 9.

Признак делимости на 10:

Если число оканчивается цифрой 0, то оно разделится на 10.

Это единственный признак делимости, рассмотренный в учебнике математики для 4 класса в виде: «Чтобы число разделилось без остатка на 10, достаточно, чтобы в его записи на конце был хотя бы один нуль».

Следует отметить, что данное требование не только достаточное условие, но и необходимое.

Как следствие этого признака делимости, можно рассматривать признак делимости без остатка на 100 (1000): для делимости числа на разрядную единицу нужно, чтобы число имело такое же количество нулей на конце.

Признак делимости на 6: ^N

Если число делится одновременно на 2 и на 3, то оно разделится на 6.

Аналогичным образом можно определить делимость на 8. Она следует из одновременной делимости на 2 и на 4.

Вопрос о делимости натуральных чисел предполагает, что речь идет о делении нацело, т. е. без остатка. Таким образом, он предваряет знакомство детей с понятием «деление с остатком».

Деление с остатком

Тема «Деление с остатком» предваряет знакомство с письменным алгоритмом деления (в столбик). С математической точки зрения деление с остатком является более общим случаем, чем деление без остатка. Деление без остатка получается в случае равенства остатка нулю. Однако в связи с тем, что в начальной школе действие деления рассматривается как действие, обратное умножению, дети сначала знакомятся с делением без остатка, а затем с делением с остатком.

Конкретный смысл действия деления в общем смысле раскрывается в процессе выполнения операций с предметными множествами: разбиении множества на равночисленные подмножества. При таких операциях не всегда возможно получение равночисленных подмножеств. Для того чтобы продемонстрировать это детям, учитель снова вынужден возвращаться к предметным действиям, манипулируя небольшим количеством предметов, чтобы продемонстрировать детям возможность получения неделимого остатка.

Например:

17 карандашей разложили в три коробки поровну. Сколько карандашей в каждой коробке?

Выполняя предметные действия в соответствии с заданной ситуацией, дети убеждаются в том, что выполнить такое разбиение множества карандашей невозможно. Остаются 2 карандаша, которые нельзя распределить поровну в три коробки.

На основании выполнения подобных заданий, учитель вводит новую запись, позволяющую определить роль оставшихся в процессе распределения предметов:

17:3 = 5 (остаток 2) и поясняет, что действие, записанное таким образом называют «деление с остатком».

В данной записи: 17 — делимое, 3 — делитель, 5 — неполное частное от деления 17 на 3, 2 — остаток.

Для проверки правильности выполненного деления следует:

1. Умножить неполное частное на делитель (5-3).

2. К полученному произведению прибавить остаток (15 + 2 = 17). В буквенном выражении данные операции соответствуют общему правилу деления с остатком:

a: b = q (ост. р), тогда а = q • b + р

В общем виде правило деления с остатком в начальной школе не рассматривается. •

Основное требование к делению с остатком:

При делении остаток всегда должен быть меньше делителя.

Это основное требование к делению с остатком. При выполнении деления с остатком всегда следует проверять выполнимость этого требования по завершении деления. Если остаток получился больше делителя, это означает, что деление выполнено неверно.

Например, при делении любого числа на 7 остаток может быть 1, 2, 3,4, 5, 6. Но не может быть 8 или 9.

Для закрепления понимания данной закономерности учитель предлагает детям задания вида:

1. Какой остаток может получиться при делении натурального числа на 2; на 3; на 6?

Ответ: При делении на 2 остаток может быть только 1; при делении на 3 — остаток может быть 2 и 1; при делении на 6 остаток может быть 1, 2, 3, 4, 5.

2. Ученик выполнил деление 144: 15 = 8 (ост. 24). В чем заключается его ошибка? Исправьте ошибку.

Ответ: Остаток должен быть меньше делителя, а в данном случае 24 >15, значит, деление выполнено неверно.

3. Найдите делимое в примерах:

а: 12 = 3 (ост. 1) b: 26 = 7 (ост. 4) Ответ: По общему правилу деления с остатком а=12-3+1 = 36+1 = 37=26.7 + 4= 182 + 4= 186.

4. Найдите делители в примерах:

56: а= 11 (ост. 1) 93: b = 2 (ост. 3)

Ответ: По общему правилу деления с остатком

а- 11 + 1 = 56; а- 11 = 56 - 1; а- 11 = 55; а= 55: 11; а= 5

b- 2 + 3 = 93; b- 2 = 93 - 3; b- 2 = 90; b= 90: 2; b= 45

Для нахождения результатов деления с остатком в начальной школе используют два основных приема:

1) При делении вида 27:5 основным приемом нахождения результата является опора на таблицу умножения. В качестве неполного частного подбирается такое значение множителя, чтобы при умножении на 5 (на делитель) получалось число, ближайшее к 27 (делимому). В данном случае — это число 5. Остаток в таком случае равен 2, что удовлетворяет основному требованию к делению с остатком.

Например:

Раздели 34: 9.

Подбираем значение частного так, чтобы при умножении его на 9 получилось число, ближайшее к 34. Это 3. Проверим 9 • 3 = 27. Найдем остаток 34 - 27 = 7. Сравним его с делителем 7 < 9.

Значит, 34: 9 = 3 (ост. 7).

Если ребенок лучше помнит таблицу деления, то можно ориентироваться на нее. В этом случае рассуждения будут несколько иными. Например:

Раздели 34: 9.

Вспомним самое большое число до 34, которое делится на 9. Это 27. 27: 9 = 3. Проверим остаток: 34 - 27= 7. 7 < 9, значит, деление выполнено верно. 34: 9 = 3 (ост. 7)

2) При делении с остатком вида 85: 15 применяется прием подбора частного с проверкой, поскольку этот случай не может опираться на знание табличного умножения или деления. В этом случае примерную цифру частного следует проверять умножением до тех пор, пока не подберется цифра, умножение которой на делитель даст в результате число, близкое к делимому.

Например:

Раздели 85: 15.

При подборе цифр частного следует применять все рациональные приемы, оговоренные ранее. В данном случае можно использовать прием округления: число 15 округляем до 20 и сразу проверяем цифру 4: 20 • 4 = 80 < 85 — не подходит. Проверяем цифру 5 сразу на делителе: 15 • 5 = 75. Находим остаток: 85 - 75 = 10 < 15.

Значит деление закончено и выполнено верно: 85; 15 = 5 (ост. 10).

В новом учебнике математики для 3 класса рассмотрен особый случай вида 3: 4. Рассмотрение таких случаев является необходимой подготовкой к обучению делению в столбик, поскольку могут попадаться случаи, когда неполное делимое не делится на делитель, и в этом случае в частном в данном разряде записывается 0.

Например:

Раздели 612: 6.

При делении данного числа имеем 6 сот.: 6 = 1 сот.

1 дес. нельзя разделить на 6 так, чтобы в частном получились десятки, поэтому в разряде десятков запишем 0, добавим к 1 дес. еще 2 ед. и разделим 12: 6 = 2.

2 единицы запишем в разряд единиц. Таким образом 612:6 = 102.

Выполнить этот случай письменного деления невозможно с полным осознанием смысла процесса, если ребенок не знаком со случаями получения нулей в неполном частном.

Для знакомства с этими случаями рассматривают деление вида 3:4.

Рассуждают следующим образом: 3 нельзя разделить на 4 так, чтобы получить целые единицы в частном, поэтому в частном запишем 0, а неразделенное число 3 запишем в остаток:

3:4 = 0 (ост. 3)

В новом учебнике математики для 3 класса при знакомстве с делением с остатком вводится новый вид записи действия деления — «уголок»:

Этот вид записи ребенок будет в дальнейшем использовать при письменном делении. Здесь эта запись используется в ознакомительном плане.

4. Приемы устных вычислений умножения и деления трехзначных и многозначных чисел

Приемы устных вычислений с трехзначными и многозначными числами касаются действий умножения и деления с числами, оканчивающимися нулями.

Прием вычислений для случаев вида 200-3; 800:4; 800:200

В этом случае целые сотни (или тысячи в примерах вида 4 000 • 3) рассматриваются как разрядные единицы, что позволяет свести эти случаи к табличному умножению и делению:

200-3 800:4 800:400

2 сот. -3 = 6 сот. 8 сот.: 4 = 2 сот. 8 сот.: 4 сот. = 2

200 • 3 = 600 800: 4 = 200 800: 400 = 2

Прием вычисления для случаев вида 70 6; 320: 8; 4 800: 800

В этом случае целые десятки (или сотни) также рассматриваются как разрядные единицы, что позволяет свести эти случаи либо к табличному умножению и делению, либо применять к ним приемы устного внетабличного умножения и деления в пределах 100.

Например:

70-6 320:8 4 800:800

7 дес. • 6 = 42 дес. 32 дес.: 8 = 4 дес. 48 сот.: 8 сот. = 6 70 • 6 = 420 320: 8 = 40 4 800: 800 = 6

При хорошем владении разрядным и десятичным составом чисел дети без труда осваивают эти приемы самостоятельно. Для подведения ребенка к осознанию смысла этих приемов можно использовать примера — помощники:

Например:

Вычисли:

4-7 40-70 140:2

40-7 14:2 140:20

Прием вычисления для случаев вида 840: 2; 560: 4; 303 • 2; 180 -4

8 подобных случаях необходимо использовать как знание десятичного состава чисел, так и приемы устного внетабличного умножения и деления в пределах 100.

Например:

840:2

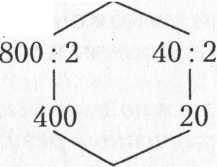
Приемы умножения и деления

на разрядную единицу

(умножения и деления на 10, 100, 1 ООО)

Умножение на разрядную единицу переводит число в следующие разряды. Технически такое умножение добавляет нули справа в запись числа, что увеличивает количество содержащихся в нем разрядов на количество добавленных нулей.

Например:

65-10 = 650 43-100 = 4300 75 -1 000 = 75 000

Делить на 10, 100, 1 000 в области натуральных чисел можно только числа, содержащие соответствующее количество младших разрядов, не имеющих значащих цифр. Технически при этом как бы убирают соответствующее количество нулей справа, начиная с последнего. Например:

650:10 = 65 8600: 100 = 86 71 000:1 000 = 71

4500:10 = 450 123 000:100= 1 230 Во всех остальных случаях деления на разрядную единицу в области натуральных чисел будет получаться деление с остатком. Например:

642:10 = 64 (ост. 2) 5 140: 100 = 51 (ост. 40)

Лекция 13

⇐ Предыдущая 15 16 17 18 192021 22 23 24 Следующая ⇒

Воспользуйтесь поиском по сайту: