 |
Потеря устойчивости внецентренно сжатых стержней
|
|
|
|
|
При действии на стержень только продольной силы N, но приложенной к продольной оси с эксцентриситетом 
, стержень будет внецентренно сжат (a).
Если к стержню приложена осевая сила N и поперечная нагрузка Q, изгибающая стержень, стержень будет сжато-изогнут. (б). Различие в работе внецентренно сжатых и сжато-изогнутых стержней незначительно, поэтому сжато-изогнутые стержни рассматриваются как внецентренно сжатые с эксцентриситетом приложения силы 
.
При определенных значениях N и M внецентренно сжатые стержни также теряют устойчивость, причем критическая сила N будет меньшей, чем при центральном сжатии, поскольку потере устойчивости способствует изгибающий момент. Изгибающий момент изменяет поведение внецентренно сжатого стержня по сравнению с центрально сжатым. По мере увеличения продольной силы первоначальный прогиб стержня увеличивается, в сечении развиваются пластические деформации и для восприятия увеличивающегося изгибающегося момента необходимо уменьшить продольную силу. Условие устойчивости внецентренно сжатого стержня можно записать так:
,
или в удобной форме сравнения напряжений с расчетным сопротивлением:
,
где 
– коэффициент понижения напряжения при внецентренном продольном изгибе.
Коэффициент зависит от условной гибкости стержня:
,
и приведенного эксцентриситета 
,
где 
- коэффициент, учитывающий развитие пластических деформаций в стержне при потере устойчивости;
- относительный эксцентриситет,
; 
-радиус ядра сечения,
- определяются по таблицам, приведенных в нормах проектирования,
- дает завышенные результаты, идущие в запас.
В плоскости, перпендикулярной к плоскости действия момента (в которой нет момента), стержень должен был бы потерять устойчивость как центрально сжатый, однако, из-за развития пластических деформаций по сечению от действия момента рабочая упругая часть сечения уменьшается и стержень может потерять устойчивость досрочно. Поэтому устойчивость внецентренно сжатых стержней в плоскости, перпендикулярной к действию момента, проверяют по формуле:
|
|
|
,
где 
- коэффициент продольного изгиба при центральном сжатии относительно, оси перпендикулярной к плоскости действия момента;
С – коэффициент, меньше единицы, зависящий от формы сечения, гибкости и относительного эксцентриситета; определяется по указаниям, приведенным в нормах проектирования.
24 Что называется критической силой и критическим напряжением?
Критическая сила (Fкр) – нагрузка, превышение которой вызывает потерю устойчивости первоначальной формы (положения) тела. С момента наступления критического состояния до момента разрушения деформации системы нарастают крайне быстро, и практически нет времени принять меры по предотвращению грозящей катастрофы. Таким образом, при расчете на устойчивость критическая нагрузка подобна разрушающей при расчете на прочность. При этом условие устойчивости можно записать в следующем виде: Fmax ≤ Fкр, или в напряжениях σmax ≤ [σу ]= Fкр A.
Критическое напряжение – это напряжения, соответствующего критической силе при потере устойчивости сжатого стержня.
Вспомним, что 
- квадрат минимального радиуса инерции.
Тогда формулу можно записать так:
Величина 
, называется гибкостью стержня.
Окончательно получаем:
25 Какой вид имеет формула Эйлера для определения критической силы?
Формула Эйлера имеет вид:
По ней можно вычислить критическую силу 
при выпучивании стержня в одной из двух главных его плоскостей, т.к только при этом условии справедливо уравнение 
, а следовательно и формула.
|
|
|
26 Как влияют жесткость стержня на изгиб, длина и условия закрепления концов стержня на значение критической силы?
Формула Эйлера была получена путем интегрирования приближенного дифференциального уравнения изогнутой оси стержня при определенном закреплении его концов (шарнирно-опертых). Значит, найденное выражение критической силы справедливо лишь для стержня с шарнирно-опертыми концами и изменится при изменении условий закрепления концов стержня.
Закрепление сжатого стержня с шарнирно-опертыми концами мы будем называть основным случаем закрепления. Другие виды закрепления будем приводить к основному случаю.
Если повторить весь ход вывода для стержня, жестко защемленного одним концом и нагруженного осевой сжимающей силой на другом конце, то мы получим другое выражение для критической силы, а следовательно, и для критических напряжений.
Расчетная схема стержня с жесткозакрепленным одним концом.
Пусть при достижении силой Р критического значения колонна будет сохранять равновесие при слабом выпучивании по кривой АВ. Сравнивая два варианта изгиба видим, что изогнутая ось стержня, защемленного одним концом, находится совершенно в тех же условиях, что и верхняя часть стержня двойной длины с шарнирно-закрепленными концами.
Значит, критическая сила для стойки длиной 
с одним защемленным, а другим свободным концами будет та же, что для стойки с шарнирно-опертыми концами при длине 
:
Если мы обратимся к случаю стойки, у которой оба конца защемлены и не могут поворачиваться, то заметим, что при выпучивании, по симметрии, средняя часть стержня, длиной 
, будет работать в тех же условиях, что и стержень при шарнирно-опертых концах (так как в точках перегиба С и D изгибающие моменты равны нулю, то эти точки можно рассматривать как шарниры).
Расчетная схема с жестко закреплеными торцами.
Поэтому критическая сила для стержня с защемленными концами, длиной , равна критической силе для стержня основного случая длиной :
Полученные выражения можно объединить с формулой для критической силы основного случая и записать:
Здесь 
— так называемый коэффициент длины, равный:
|
|
|
при шарнирных концах (основной случай) 
,
одном свободном, другом защемленном 
,
обоих защемленных концах 
.
Для стержня, изображенного на рис.4, с одним защемленным, а другим шарнирно-опертым концами, коэффициент оказывается примерно равным 
, а критическая сила:
Потеря устойчивости стержня с одним жесткозакрепленным и другим шарнирно-опорным торцом
Величина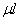 
называется приведенной (свободной) длиной, при помощи коэффициента длины любой случай устройства опор стержня можно свести к основному; надо лишь при вычислении гибкости вместо действительной длины стержня ввести в расчет приведенную длину 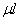. Понятие о приведенной длине было впервые введено профессором Петербургского института инженеров путей сообщения Ф. Ясинским.
На практике, однако, почти никогда не встречаются в чистом виде те закрепления концов стержня, которые мы имеем на наших расчетных схемах.
Вместо шаровых опор обычно применяются цилиндрические шарниры. Подобные стержни следует считать шарнирно-опертыми при выпучивании их в плоскости, перпендикулярной к оси шарниров; при искривлении же в плоскости этих осей концы стержней следует считать защемленными (с учетом оговорок, приведенных ниже для защемленных концов).
27 Что называется гибкостью стержня? От каких параметров сжатой стойки она зависит?
Понятие гибкости стержня: λ = μl / imin. Это безразмерная величина, характеризующая размеры стержня и способ закрепления его концов. Окончательно получим:
Σкр = π2Е / λ2.
Формулу Эйлера можно применять только при выполнении условия:
Σкр = π2Е / λ2 ≤ σпц,
где: σпц – предел пропорциональности материала стержня. Следовательно, должно быть
λ ≥ √(π2Е / σпц) = λпред (здесь √ - знак квадратного корня).
Величину, стоящую в правой части неравенства, называют предельной гибкостью. Предельная гибкость зависит только от физико-механических свойств материала стержня.
Условие применимости формулы Эйлера можно записать так: λ ≥ λпред, т. е. формула Эйлера применима лишь в тех случаях, когда гибкость стержня больше или равна предельной гибкости. Так, для стержней из низкоуглеродистой стали формула Эйлера применима, если их гибкость λ ≥ 100.
|
|
|
В тех случаях, когда гибкость стержней меньше предельной, формула Эйлера становится неприменимой и при расчетах пользуются эмпирической формулой Ясинского:
Σкр = a – bλ,
где: а и b – коэффициенты, зависящие от материала и определяемые по таблицам справочников.
Если стержень имеет гибкость λ ≤ 40, то его можно рассчитывать на простое сжатие по формуле σс = F / А.
28 В какой диапазоне гибкости можно использовать Эйлера? Как устанавливается предел ее применимости?
Вывод формулы Эйлера основан на интегрировании дифференциального уравнения упругой линии стержня. Это уравнение справедливо только в пределах линейной зависимости между напряжениями и деформациями, поэтому и формула Эйлера применима только до тех пор, пока критические напряжения, определяемые по этой формуле, не превосходят предела пропорциональности, т. е. при условии:
Используя соотношение — наименьший радиус инерции поперечного сечения стержня, можем записать это условие так:
Безразмерная величина X называется гибкостью стержня:
29 Какой вид имеет график зависимости критических напряжений от гибкости стержня?
График зависимости критических напряжений от гибкости стержня представлен на рисунке.
30 Какие формы поперечного сечения сжатого стержня являются рациональными с точки зрения устойчивости?
При проектировании стержней, работающих на устойчивость, следует выбирать такую форму сечения, чтобы гибкость стержня была одинаковой относительно обеих главных осей его сечения (условие равноустойчивости), а значит, максимальный и минимальный моменты инерции такого сечения должны быть одинаковы Jmax = Jmin. Кроме того, необходимо стремиться к получению при данной площади наибольших радиусов инерции. Для этого необходимо разместить материал сечения по возможности дальше от центра тяжести (трубчатые, коробчатые сечения). По степени рациональности известные сечения можно распределить следующим образом: трубчатое сечение, уголок, двутавр, швеллер, квадрат, круг, прямоугольник.
Вопросы к Задаче 6
31 Как записывают интеграл О.Мора для определения перемещений при изгибе?
Интеграл Мора позволяет определять прогибы и углы поворота заданного сечения балки, используя интегральное исчисление. Хотя данный метод предпочтительнее метода начальных параметров, он неудобен из-за необходимости вычисления интеграла. Из интеграла Мора был получен удобное для практического применения правило Верещагина, при котором не нужно вычислять интегралы, а только нужно находить площадь и центр тяжести эпюр.
|
|
|
Формула для получения интеграла Мора:
32 Какова последовательность определения линейных и угловых перемещений с использованием интеграла О.Мора?
1) К вспомогательной балке в той точке, где требуется определить перемещение, прикладываем единичное усилие. При определении прогиба прикладываем единичную силу 
, а при определении угла поворота – единичный момент 
;
2) для каждого участка балки составляем выражения для изгибающих моментов заданной (
) и вспомогательной (
) балок;
3) вычисляем интеграл Мора для всей балки по соответствующим участкам;
- если вычисленное перемещение имеет положительный знак, то это означает, что его направление совпадает с направлением единичного усилия. Отрицательный знак указывает на то, что действительное направление искомого перемещения противоположно направлению единичного усилия.
33 Что означает знак «минус» вычисленного значения интеграла О.Мора?
Отрицательный знак указывает на то, что действительное направление искомого перемещения противоположно направлению единичного усилия.
34 В каких случаях при вычислении перемещений методом О.Мора можно применить формулу Симпсона? Как записывают формулу Симпсона?
Для определения любого перемещения (линейного или углового) в методе Мора балка рассматривается в двух состояниях: действительном и вспомогательном. Вспомогательное состояние получается следующим образом: сначала всю заданную нагрузку нужно удалить, затем приложить «единичный силовой фактор» в том месте, где требуется определить перемещение, и по направлению этого искомого перемещения. Причем, когда определяем линейное перемещение (прогиб балки), то в качестве «единичного силового фактора» принимается сосредоточенная сила 
, а если требуется найти угол поворота, то приложить следует сосредоточенную пару 
.
Во многих случаях интегрирования по Мору можно избежать и применить способ «перемножения» эпюр. Одним из таких способов является способ Симпсона, по которому значение интеграла Мора на участке длиной ℓ вычисляется по следующей формуле:
Здесь обозначено: a, b и с – соответственно крайние и средняя ординаты эпюры изгибающих моментов действительного состояния М,
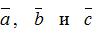- крайние и средняя ординаты эпюры изгибающих моментов, но только вспомогательного состояния.
|
|
|
