 |
Линейное обнаружение
|
|
|
|
Варианты задания
1. Статистика 
, независимые 
, 
,
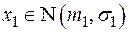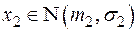. Проверить гипотезу H: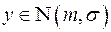 
, 
, 
.
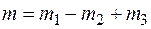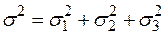2. Статистика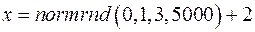 
. Проверить гипотезу H: 
.
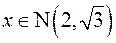3. Статистика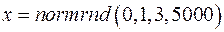 
. Проверить гипотезу H: 
.
4. Проверить гипотезу о величине 
, генерируемой функцией RAND: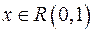 
.
5. Распределение Релея: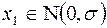 
, 
, 
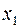и 
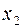независимы; 
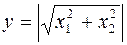. Проверить гипотезу 
.
6. Распределение Максвелла: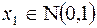 
, 
, 
, , , 
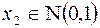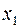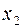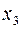независимы; 
.
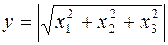Проверить гипотезу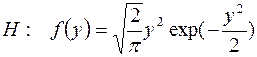 
.
7. Проверить гипотезу о величине , генерируемой функцией RANDN: 
.
8. Распределение арксинуса: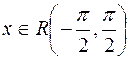 
, 
.
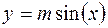Проверить гипотезу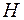 
:
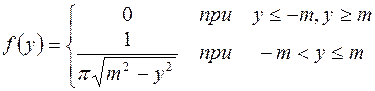
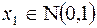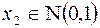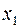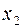9. Показательное распределение: , , и независимы;
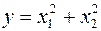. Проверить гипотезу : 
, 
.
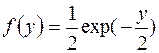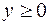10. 
- распределение: независимые 
, 
;
, 
, .
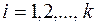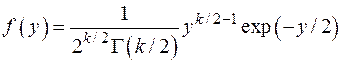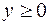Проверить гипотезу 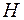для одной степени свободы (
):
.
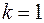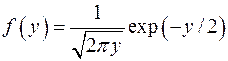Гамма- функция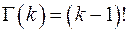 
вычисляется функцией 
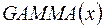. Частные случаи: 
, 
, 
, 
, 
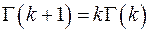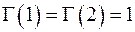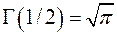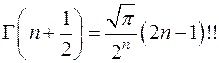
11. Проверить гипотезу 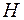для - распределения с двумя степенями свободы (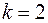
, экспоненциальное распределение):
.
12. Проверить гипотезу 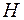для - распределения с четырьмя степенями свободы (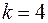
):
.
13. Гамма – распределение:
.
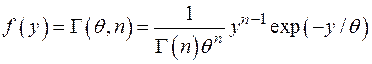При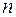 
- целом это распределение называется распределением Эрланга порядка 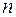, описывающим сумму независимых случайных величин с распределением
.
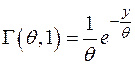Проверить гипотезу о распределении Эрланга с двумя степенями свободы.
14. Проверить гипотезу о распределении Эрланга с тремя степенями свободы.
15. Проверить гипотезу о том, что гамма – распределение 
есть - распределение с 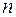степенями свободы для случая 
.
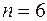16. Распределение Стъюдента: 
, 
, 
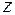и 
независимы;
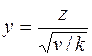. Проверить гипотезу :
, 
.
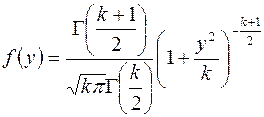17. Распределение Фишера (Снедекора):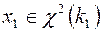 
, 
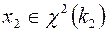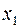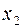, и независимы; 
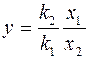. Проверить гипотезу :
, 
.
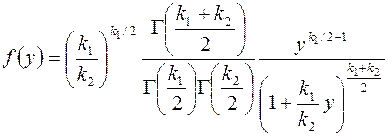18. Нецентральное - распределение с степенями свободы имеет плотность
,
- параметр нецентральности. Оно описывает сумму 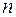независимых величин
, 
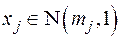- сумма квадратов математических ожиданий.
|
|
|
Проверить гипотезу о нецентральном - распределении с одной степенью свободы и параметром нецентральности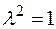 
.
19. Проверить гипотезу о нецентральном - распределении с тремя степенями свободы; параметр нецентральности 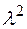задать самостоятельно.
20. Проверить гипотезу о нецентральном - распределении с пятью степенями свободы; параметр нецентральности 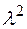задать самостоятельно.
21. Проверить гипотезу о нецентральном - распределении с двумя степенями свободы
,
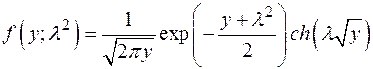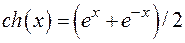- гиперболический косинус. Параметр нецентральности 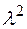задать самостоятельно.
22. 
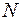- мерный случайный вектор 
. Задана квадратичная форма
.
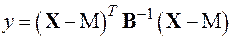Проверить гипотезу о том, что величина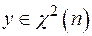 
для случая 
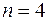; вектор средних 
и корреляционную матрицу 
задать самостоятельно.
23. Выборочное среднее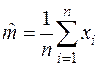 
, независимые 
. Задана статистика 
. Проверить гипотезу : 
. Параметры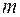 
, 
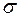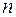, задать самостоятельно.
24. Выборочня дисперсия 
, независимые . Задана статистика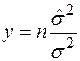 
. Проверить гипотезу : 
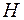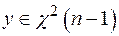. Параметры 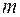, , 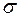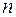задать самостоятельно.
25. Статистика 
, независимые 
, 
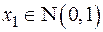. Проверить гипотезу H: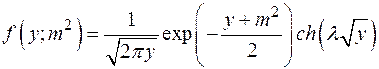 
.
MATLAB – функции:
NORMCDF(X,M,SIGMA) – нормальное распределение;
UNICDF(X,A,B) – равномерное распределение от A до B;
RAYLCDF(X,B) – распределение Релея с параметром B =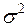 
;
EXPPDF(X,MU) – показательное распределение с параметром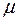 
(плотность распределения 
);
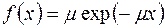CHI2CDF(X,V) - - распределение с V степенями свободы;
NCX2CDF(X,N,L) – нецентральное - распределение с 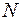степенями свободы и параметром нецентральности L;
TCDF(X,V) - распределение Стъюдента с V степенями свободы;
FCDF(X,K1,K2) - распределение Фишера с K1 и K2 степенями свободы.
Пример. Статистика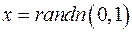 
. Проверить гипотезу H: 
.
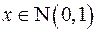Программа
N=5000
del=0.5
x=-3:del:3;
f=normpdf(x,0,1)
y=randn(1,N);
H=hist(y,x)
hh=hist(y,x)/N/del % гистограмма для рисунка
h=hist(y,x)/N % гистограмма для расчета вероятностей
plot(x,f)
hold on
stem(x,hh)
рассчитывает теоретическую плотность распределения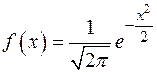 
и
гистограмму (рис. 1).
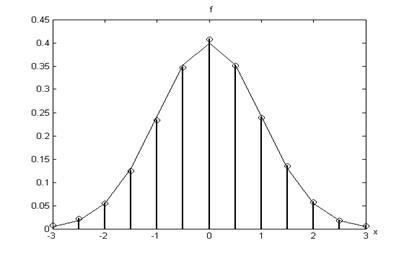
Рис. 1. Плотность распределения и гистограмма
|
|
|
Расчеты вероятностей попадания в интервалы дискретизации должны выполняться с функцией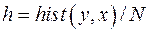 
. Применение функции 
требует сдвига на полинтервала:
F=normcdf(x+del/2,0,1) % сдвиг на полинтервала
p=diff(F)
ppp=sum(p)
pp=sum(h)
dH=diff(cumsum(h))
n=length(dH)
P=[p;dH]
0.0092 0.0278 0.0656 0.1210 0.1747 0.1974 0.1747
0.0106 0.0276 0.0620 0.1168 0.1732 0.2036 0.1752
0.1210 0.0656 0.0278 0.0092 0.0024
0.1194 0.0674 0.0284 0.0092 0.0032
Критерий 
:
hi=N*sum((p-dH).^2./p)
hi0=chi2inv(0.95,11)
дает результат = 5.4804 при критическом значении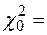 
19.6751. Гипотеза не отвергается.
Пример расчета вероятности попадания величины, распределенной по закону Максвелла, в интервал (a,b).
syms x
f=sqrt(2/pi)*x^2*exp(-x^2/2) % плотность Максвелла
F=int(f) % функц. распред. Максвелла
ezplot(F,0,4)
a=1
b=1.5
p=int(f,a,b) % вероятность попадания в интервал (a,b)
p = (7186705221432913/18014398509481984*2^(1/2)*erf(3/4*2^(1/2))-7186705221432913/18014398509481984*2^(1/2)*erf(1/2*2^(1/2)))*pi^(1/2)-21560115664298739/18014398509481984*exp(-9/8)+
+7186705221432913/9007199254740992*exp(-1/2) = 0.2791.
Литература
1. Соколов Г.А, Гладких И.М. Математическая статистка. - М.: Экзамен, 2007. –
431 с.
2. Ивченко Г.И., Медведев Ю.И. Математическая статистика. - М.: Высшая школа, 1984. – 248 с.
3. Чистяков В.П. Курс теории вероятностей. - М.: Наука, 1982. – 256 с.
Лабораторная работа № 2
ГЕНЕРАТОР ВЕКТОРНЫХ РЕАЛИЗАЦИЙ
СЛУЧАЙНОГО ПРОЦЕССА
Цель работы: освоение аппарата сингулярного разложения корреляционной матрицы для генерирования псевдослучайных векторов с заданными корреляционными свойствами.
1. Методические указания
Линейный фильтр может описываться не только весовой функцией, но и оператором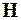 
- матрицей, которая преобразует вектор 
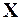в вектор 
по правилу
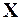= . (1)
Получая последовательно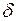 
- коррелированные векторы 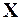размерностью чисел и преобразовывая их по правилу (1), можно построить генератор векторов той же размерности, но уже окрашенных в соответствии с оператором 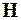. Таким образом, задача синтеза генератора сводится к задаче расчета нужного оператора .
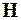Генератор полубесконечных реализаций задается интегральным уравнением
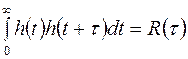. (2)
Его векторный аналог
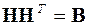, (3)
в котором 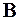- корреляционная матрица заданного векторного процесса, определяет искомый оператор 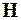. Его решение
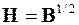. (4)
Действительно, так как корреляционная матрица - симметричная квадратная матрица, то и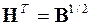 
, что и дает равенство (3).
|
|
|
Корень квадратный из корреляционной матрицы [1,2] вычисляется следующим образом.
Корреляционная матрица (по определению невырожденная) может быть записана в виде сингулярного разложения (разложения по собственным векторам 
), называемого также разложением Такаги [2]:
,
где 
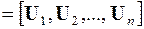- матрица вектор - столбцов 
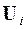- собственных векторов матрицы ;
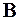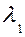0 0...... 0
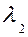= 0 
0...... 0 -
................
0 0 0.....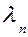 
 |
- диагональная матрица собственных значений матрицы 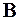. Собственные векторы ортонормированы:
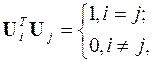
собственные значения 
> 0,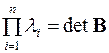 
.
Если определить
,
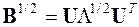то произведение
.
Таким образом, согласно (4), оператор генератора векторных сигналов с корреляционной матрицей 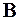, формирующего их по правилу (1), есть
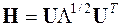. (5)
Оператор можно записать еще короче:
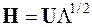, (6)
так как и форма (6) обращает уравнение (3) в тождество.
Аппарат собственных векторов позволяет решать более сложные задачи “перекрашивания” шума - преобразовывать окрашенный шум в окрашенный. В пространстве непрерывных процессов эта задача описывается интегральным уравнением [3], обобщающим уравнение (2),
, (7)
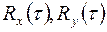- соответственно функции корреляции преобразуемого и нужного стационарных процессов. Если (1) записать
= 
,
то матрица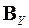 
рассеяния вектора представляется соотношением
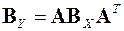, (8)
являющимся векторным аналогом уравнения (7). Его можно записать
,
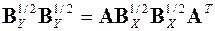откуда следует
, 
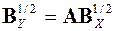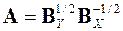. (9)
Кроме основного решения (9) уравнение (8) имеет следующие:
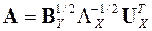, (10)
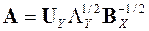, (11)
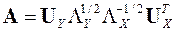(12)
Таким образом, генератор векторных случайных процессов определяется операторами (5),(6), если преобразуется 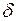- коррелированный процесс, или операторами (9) - (12), если преобразуется окрашенный процесс.
В современном математическом обеспечении ЭВМ имеются весьма точные процедуры вычисления собственных векторов и собственных значений матриц. Например, в системе “MATLAB” оператор
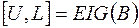
предписывает вычисление матриц U = и L = 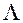с погрешностями порядка 10 
.
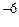Пример. Заданы корреляционные матрицы
1,000 0,607 0,368 0,223 0,105
0,607 1,000 0,607 0,368 0,223
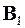= 0,368 0,607 1,000 0,607 0,368,
0,223 0,368 0,607 1,000 0,607
0,105 0,223 0,368 0,607 1,000
1,000 - 0,607 0,368 - 0,223 0,105
- 0,607 1,000 - 0,607 0,368 - 0,223
|
|
|
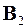= 0,368 - 0,607 1,000 - 0,607 0,368.
- 0,223 0,368 - 0,607 1,000 - 0,607
0,105 - 0,223 0,368 - 0,607 1,000
Собственные значения обеих матриц одинаковы: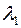 
= 0,2628,
= 0,3576,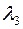 
= 0,5412, 
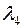= 1,1694, 
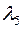= 2,6690.
Собственные векторы матриц отличаются знаками некоторых элементов:
0,2411 - 0,4111 - 0,5493 - 0,5753 0,3743
- 0,5111 0,5753 0,1013 - 0,4111 0,4780
= 0,6010 0 0,6132 0 0,5127,
- 0,5111 - 0,5753 0,1013 0,4111 0,4780
0,2411 0,4111 - 0,5493 0,5753 0,3743
0,2411 0,4111 - 0,5493 - 0,5753 0,3743
0,5111 0,5753 - 0,1013 - 0,4111 - 0,4780
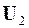= 0,6010 0 0,6132 0 0,5127.
0,5111 - 0,5753 - 0,1013 0,4111 - 0,4780
0,2411 - 0,4111 - 0,5493 - 0,5753 0,3743
Задача расчета оператора , преобразующего 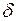- коррелированный процесс с единичной матрицей рассеяния в процесс с матрицей рассеяния 
, и оператора 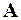, преобразующего процесс с 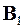в процесс с 
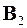, имеет восемь решений. Одно из них: расчет по формуле (6) дает
0,1236 - 0,2458 - 0,4041 - 0,6221 0,6115
- 0,2620 0,3440 0,0745 - 0,4446 0,7809
= 0,3081 0 0,4511 0 0,8376;
- 0,2620 - 0,3440 0,0745 0,4446 0,7809
0,1236 0,2458 - 0,4041 0,6221 0,6115
расчет по формуле (9)
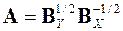
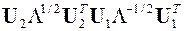
дает оператор
1,2363 - 0,8370 0,2746 - 0,1748 0,0746
0,6946 1,4469 - 0,7511 0,2852 - 0,1561
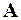= 0,2385 - 0,7659 1,4211 - 0,7659 0,2385.
- 0,1561 0,2852 - 0,7511 1,4469 - 0,6946
0,0746 - 0,1748 0,2746 - 0,8240 1,2363
2. Порядок выполнения работы
1. Записывается матрица рассеяния 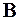стационарного шума размерностью 
= 5 - 9.
2. Вычисляются собственные векторы и собственные числа; проверяются их свойства.
3. Вычисляются 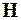- оператор окрашивания и 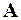- оператор “выбеливания” - преобразования окрашенного процесса в 
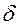- коррелированный.
4. Моделируются процессы окрашивания и “выбеливания”.
3. Содержание отчета
Результаты по пунктам 1 - 4 разд. 2.
4. Контрольные вопросы
1. Как составляется матрица рассеяния стационарного шума?
2. Каковы собственные значения матрицы рассеяния белого шума?
3. Каковы собственные значения матрицы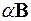 
?
4. Запишите характеристическое уравнение квадратной матрицы.
5. Каковы собственные значения матрицы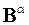 
?
6. Существует ли произвольная степень несимметричной квадратной матрицы?
Список литературы
1. Воробьёв С.Н., Осипов Л. А. Моделирование систем. - СПб.: ГУАП, 2006. –
66 с.
2. Воробьев С.Н., Осипов Л.А. Линейные системы. Расчет и моделирование. -
СПб.: ГУАП, 2004. – 122 с.
3. Гантмахер Ф.Р. Теория матриц. - М.: Наука, 1966. – 576 с.
4. Хорн Р., Джонсон Ч. Матричный анализ. - М.: Мир,1989. – 655 с.
5. Тихонов В.И. Статистическая радиотехника. - М.: Сов. радио, 1966. – 678 с.
Лабораторная работа № 3
ЛИНЕЙНОЕ ОБНАРУЖЕНИЕ
Цель работы: изучение принципов построения классических обнаружителей импульсных сигналов в аддитивном стационарном гауссовом шуме.
1. Методические указания
1.1. Рабочая характеристика.
Классическая задача обнаружения детерминированного сигнала 
, маскируемого аддитивным стационарным гауссовым шумом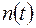 
, формулируется как задача проверки гипотезы 
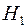против альтернативы 
[1]:
|
|
|
: 
, : + ;
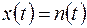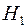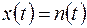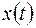- сигнал на входе, 
, 
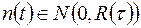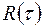- функция корреляции. Если известны функция корреляции шума, форма, амплитуда, время прихода и длительность 
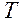сигнала, гипотезы называются простыми: неизвестно лишь, была ли на входе в интервале 
сумма шума и сигнала или наблюдался только шум. Итак:
: 
, : 
.
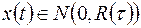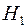Отрезок входного сигнала на известном интервале по некоторому линейному правилу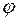 
преобразуется в число 
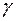, называемое статистикой проверки гипотез:
.
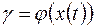Так как преобразование линейно, статистика распределена по нормальному закону:
, 
.
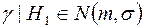Плотности распределения статистики при обеих гипотезах показаны на рис.1 для отношения сигнал – шум 
.
Процедура обнаружения, таким образом, сводится к разбиению пространства значений статистики критическим уровнем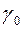 
(пороговым уровнем) на две области: если статистика 
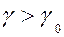, принимается решение в пользу гипотезы 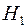, если 
- в пользу гипотезы .
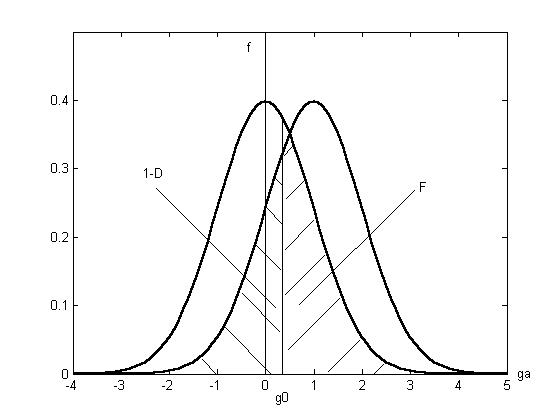
Рис.1. Плотности распределения
Решения могут быть правильными или ошибочными. Вероятность ошибки первого рода (вероятность ложной тревоги)
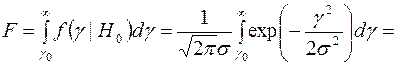
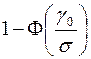, (1)
вероятность ошибки второго рода (вероятность пропуска сигнала)
.
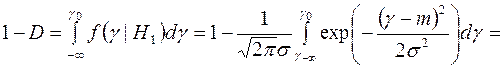
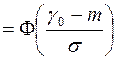Вероятность правильного решения при гипотезе 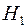- вероятность обнаружения равна
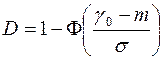, (2)
-
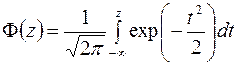- интеграл вероятности.
Функциональная зависимость вероятности обнаружения от вероятности ложной тревоги
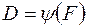
называется рабочей характеристикой [2] обнаружителя (рис. 2).
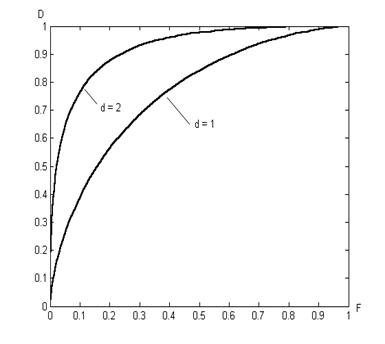
Рис. 2. Рабочие характеристики
Рабочая характеристика строится расчетом вероятностей по формулам (1) и (2) при изменении критического уровня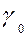 
от = 
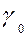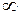до 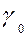= - 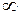. Рабочая характеристика полностью характеризует эффективность обнаружителя. Чем выше крутизна рабочей характеристики на начальном участке, тем выше качество обнаружения. В свою очередь, крутизна рабочей характеристики тем больше, чем больше отношение сигнал - шум (по мощности)
,
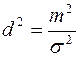характеризующее относительный сдвиг плотностей распределения статистики при различных гипотезах. Например, рабочая характеристика на рис. 2 соответствует значению 
= 1, что обеспечивает при вероятности ложной тревоги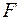 
= 0,1 вероятность обнаружения 
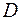= 0,39. При отношении сигнал - шум = 4 значению 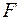= 0,1 соответствовала бы вероятность обнаружения 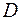= 0,76 и т. д.
1.2. Критерии проверки гипотез
Проверка гипотез, как любая задача математической статистики, предполагает ее оптимальное решение. Понятие оптимальности включает и правило формирования линейной статистики, и правило назначения критического уровня 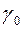. Первое связано с максимизацией крутизны рабочей характеристики, второе - с выбором рабочей точки, то есть с назначением критического уровня.
Пусть заданы априорные вероятности гипотез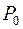 
и 
и матрица стоимости решений
=,
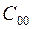
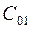
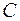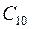
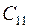
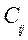- стоимость принятия решения в пользу гипотезы 
при правильной гипотезе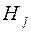 
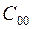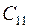(, - стоимость правильных решений; 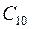- стоимость ложной тревоги, 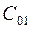- стоимость пропуска сигнала). Средняя стоимость решения равна
.
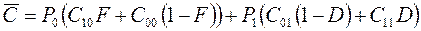Критерий (правило) Байеса (минимума среднего риска) предписывает выбор рабочей точки, минимизирующей среднюю стоимость [2]. Минимум среднего риска достигается, если решение в пользу гипотезы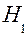 
принимается при условии
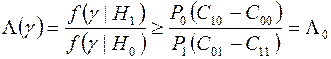, (3)
в котором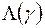 
- отношение правдоподобия, 
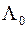- критический уровень. Например, в двоичном симметричном канале:
- вероятности ошибок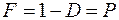 
;
- априорные вероятности 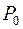= = 0,5;
- стоимости решений 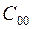= 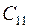, 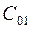= 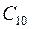, можно положить 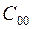= 0, 
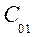=1;
тогда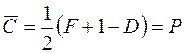 
, минимум среднего риска обеспечивается минимумом вероятности ошибки при значении критических уровней 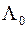=1,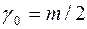 
(рис.2).
Альтернативный критерий Неймана - Пирсона [1,2] применяется, если априорные вероятности и стоимости решений неизвестны, напри-
мер, в радиолокации. Критерий Неймана - Пирсона предписывает при заданном значении вероятности ложной тревоги 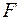максимизировать вероятность обнаружения 
. Обычно значения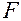 
задаются близкими к нулю, так что по критерию Неймана - Пирсона лучше тот обнаружитель, рабочая характеристика которого круче в окрестности 
.
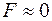Следует отметить, что при обнаружении полностью известного сигнала в аддитивном гауссовом шуме вероятност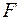и и 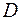связаны функционально, и максимизация вероятности обнаружения теряет смысл. Критерий Неймана - Пирсона применяется в более сложных случаях.
1.3. Согласованная фильтрация.
Оптимальное правило формирования статистики проверки простых гипотез описывается интегральным уравнением [3]
, (4)
называемым также уравнением согласованной фильтрации. Решение уравнения определяет статистику
, (5)
обладающую свойством
.
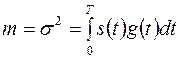Следовательно, отношение сигнал - шум для статистики равно
. (6)
Согласованный фильтр - линейный фильтр с весовой функцией
.
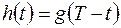Выходное напряжение согласованного фильтра
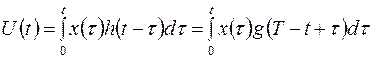
в момент окончания сигнала (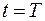
) равно статистике (5).
Согласованный фильтр обеспечивает максимальное отношение сигнал - шум, следовательно, оптимален по критерию Неймана - Пирсона.
1.4. Дискретная согласованная фильтрация.
В дискретном временном пространстве уравнение согласованной фильтрации (4) записывается
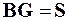, (7)
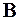- корреляционная матрица, 
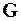- решающий вектор, 
- вектор сигнала. Уравнение (7) имеет решение всегда, так как матрица рассеяния невырожденная:
. (8)
Статистика аналогично (5) определяется произведением
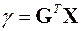. (9)
Как и в непрерывном случае, вследствие линейности процедуры (9)
, ;
,
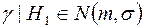. (10)
Свойства (10) дискретного согласованного фильтра аналогичны свойствам (6) согласованного фильтра. Дискретный согласованный фильтр полностью описывается рабочей характеристикой.
2. Порядок выполнения работы
1. В соответствии с заданием решается уравнение дискретной согласованной фильтрации (7).
2. Генерируются массивы векторов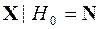 
и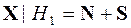 
размерностью = 5 - 9, объемом N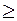 
1000.
3. Вычисляются массивы значений статистики (9) при гипотезах и .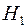
4. Строятся гистограммы статистики при гипотезах и .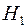
5. Строятся рабочие характеристики для нескольких значений отношения сигнал - шум.
6. Рассчитываются значения (3) критических уровней 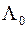при различных вариантах матрицы стоимостей и априорных вероятностей.
3. Содержание отчета
Результаты по пунктам 1 - 6 разд. 2.
4. Контрольные вопросы
1. Получите соотношения (10).
2. Как следует строить гистограммы (пункт 4 содержания отчета)?
3. В каких случаях решение (8) становится некорректным?
4. Какова минимальная вероятность обнаружения?
5. Имеют ли размерность величины из соотношения (10)?
6. Решите задачу дискретной согласованной фильтрации для 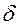- коррелированного шума.
7. Запишите отношение правдоподобия (3) для гауссовых статистик.
8. Каково решение задачи проверки простых гипотез, если сигнал имеет форму собственной функции ядра интегрального уравнения (4)?
9. Каково решение задачи дискретной согласованной фильтрации, если сигнал задан в виде собственного вектора матрицы рассеяния?
10. Может ли согласованный фильтр использоваться как измеритель времени прихода сигнала?
Список литературы
1. Ивченко Г.И. Математическая статистика. - М.:
|
|
|
