 |
Задача о покрытии множества
|
|
|
|
Постановка задачи
Задача о покрытии множества формулируется следующим образом.
Пусть M = {h1, …, hm} – некоторое множество объектов hi (i = = 1,…,m), а S = {S1, …, Sn} – семейство подмножеств Sj (j = 1,…,n), содержащих элементы множества M, и каждому из этих подмножеств поставлено в соответствие некоторое число (вес) cj. Требуется найти такой набор подмножеств S*Ì S, при котором достигается покрытие множества M с минимальным суммарным весом.
Сформулируем данную задачу в терминах булевого линейного программирования.
Пусть A = ||aij|| – булева матрица размерности m´n, элементы которой формируются исходя из условия: aij = 1, если hi Î Sj (т.е. если i-й элемент множества M содержится в подмножестве Sj), и aij = 0 – в противном случае.
Пусть xj – булева переменная, которая равна 1, если подмножество Sj входит в покрытие множества M, и равна 0 –в противном случае.
Тогда в формальном виде задача о покрытии множества может быть представлена следующим образом:
 (4.1)
(4.1)
 i = 1,…,m. (4.2)
i = 1,…,m. (4.2)
Выражение (4.2) – ограничение в виде системы линейных неравенств – задаёт условие принадлежности каждого элемента множества М покрытию.
Формулировка задания
Решить задачу о покрытии множества M = {1,2,3,4,5,6,7,8}. Семейство подмножеств данного множества и значения их весов для различных вариантов выполнения задания представлены на рисунке
| Номер вари-анта | Семейство подмножеств Sj | Веса cj подмножеств Sj |
| S1 = {2,3,5,8}; S2= {1,3,6,8}; S3 = {2,5,6,8}; S4 = {1,2,3,5}; S5= {3,5,6}; S6= {2,4,5,7}; S7 = {1,3,4,7,8}; S8= {2,3,5,6}; S9 = {1,5,7}; S10 = {1,2,5,8}; S11= {1,2,4,6,7}; S12= {2,7,8}; S13 = {1,3,6,7,8} | c1 =6; c2 =7; c3 =8; c4 =9; c5 =9; c6 =5; c7 =6; c8 =8; c9 =7; c10 =5; c11 =6; c12 =6; c13 =10 |
Код программы:
Файл 3_4_5:
clc
clear
f = [6; 7; 8; 9; 9; 5; 6; 8; 7; 5; 6; 6; 10];
A=[ 0 1 0 1 0 0 1 0 1 1 1 0 1;
1 0 1 1 0 1 0 1 0 1 1 1 0;
|
|
|
1 1 0 1 1 0 1 1 0 0 0 0 1;
0 0 0 0 0 1 1 0 0 0 1 0 0;
1 0 1 1 1 1 0 1 1 1 0 0 0;
0 1 1 0 1 0 0 1 0 0 1 0 1;
0 0 0 0 0 1 1 0 1 0 1 1 1;
1 1 1 0 0 0 1 0 0 1 0 1 1];
b = ones(8,1);
[x,fval] = bintprog(f, -A, -b) % вывод в двоичном виде
y = find(x) % номера подмножеств
Решение:
x =
fval =
y =
Таким образом, минимальное покрытие множества М образуют подмножества S1 и S11 с суммарным весом, равным 12.
Задача 5
РЕШЕНИЕ ЗАДАЧИ О МАКСИМАЛЬНОМ ПАРОСОЧЕТАНИИ
Постановка задачи
Задача о максимальном паросочетании (рёберном покрытии) формулируется следующим образом: для заданного неориентированного графа требуется найти такое подмножество E* рёбер из всего их множества E (E* Ì E) максимальной мощности, в котором никакие два ребра не будут инцидентны (т.е. не будут иметь общей вершины).
В терминах булевого линейного программирования формально данная задача формулируется следующим образом:
 (5.1)
(5.1)
 , i = 1,…,m. (5.2)
, i = 1,…,m. (5.2)
Здесь xj – переменные, ассоциированные с рёбрами, при этом xj = =1, если ребро с номером j входит в максимальное паросочетание, и xj = 0 – в противном случае.
Коэффициенты aij – компоненты булевой матрицы инцидентности А размерности m´n – принимают значение 1, если вершина с номером i инцидентна ребру с номером j, и значение 0 – в противном случае.
Выражение (5.2) – ограничение в виде системы линейных неравенств – задаёт условие того, что в каждой вершине сумма инцидентных ей переменных (рёбер) не превышает единицы.
Задача о максимальном взвешенном паросочетании отличается только целевой функцией, т.е. вместо выражения (5.1) имеет место
 (5.3)
(5.3)
где сj – вес ребра с номером j.
Формулировка задания
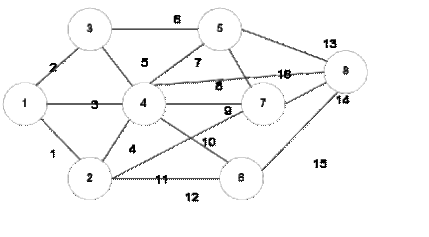
Решить задачу о максимальном взвешенном паросочетании для графа, изображённого на рисунке 5.1. Значения весов рёбер для различных вариантов выполнения задания представлены в таблице.
| Номер варианта | Значения весов рёбер | |||||||||||||||

|
|
|
Рисунок 5.1 – Неориентированный граф
Код программы:
Файл 3_4_5:
clc
clear
f = [6;8; 9; 10; 11;
7; 12; 9; 6; 7;
8; 10; 11; 7; 5; 9];
A = [ 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0;
1 0 0 1 0 0 0 0 0 0 1 1 0 0 0 0;
0 1 0 0 1 1 0 0 0 0 0 0 0 0 0 0;
0 0 1 1 1 0 1 1 1 1 0 0 0 0 0 0;
0 0 0 0 0 1 1 0 0 0 0 0 1 0 0 1;
0 0 0 0 0 0 0 0 0 1 0 1 0 0 1 0;
0 0 0 0 0 0 0 0 1 0 1 0 0 1 0 1;
0 0 0 0 0 0 0 1 0 0 0 0 1 1 1 0];
b = ones(8,1);
x = bintprog(-f, A, b);
y = find(x) % номера ребер
Решение:
y =
Таким образом, E* = {2,7,12,14}, т.е. в максимальное паросочетание входят рёбра с номерами 2,7,12,14
Задача 6
РЕШЕНИЕ ЗАДАЧИ О МИНИМАЛЬНОМ ВЕРШИННОМ ПОКРЫТИИ
Постановка задачи
Задача о минимальном вершинном покрытии формулируется следующим образом: для заданного неориентированного графа требуется найти такое подмножество V* вершин из всего их множества V (V * Ì V) минимальной мощности, которые были бы инцидентны всем рёбрам графа.
В терминах булевого линейного программирования формально данная задача формулируется следующим образом:
 (6.1)
(6.1)
 , j = 1,…,n. (6.2)
, j = 1,…,n. (6.2)
Здесь xi – переменные, ассоциированные с вершинами, при этом xi = 1, если вершина с номером i входит в минимальное вершинное покрытие, и xi = 0 – в противном случае.
Коэффициенты aji – компоненты булевой матрицы инцидентности А размерности n´m – принимают значение 1, если ребро с номером j
инцидентно вершине с номером i, и значение 0 – в противном случае.
Выражение (6.2) – ограничение в виде системы линейных неравенств – задаёт условие того, что каждому ребру инцидентна хотя бы одна вершина, т.е. сумма вершин, инцидентных каждому ребру, не меньше единицы.
Задача о минимальном взвешенном вершинном покрытии отличается только целевой функцией, т.е. вместо выражения (6.1) имеет место
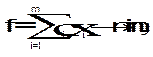 (6.3)
(6.3)
где сi – вес вершины с номером i.
Следует отметить, что данная задача является двойственной по отношению к задаче о максимальном паросочетании.
Формулировка задания
Решить задачу о минимальном взвешенном вершинном покрытии для графа, изображённого на рисунке 6.1. Значения весов вершин для различных вариантов выполнения задания представлены на рисунке.
| Номер вари-анта | Значения весов вершин | ||||||||
|
|
|
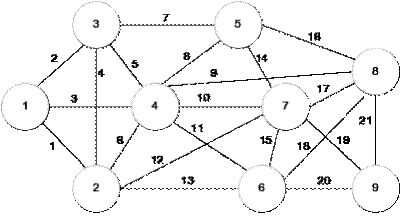

Рисунок 6.1 – Неориентированный граф
Код программы:
Файл 3_6_5:
clc
clear
f = [9; 6; 7; 8; 10; 8; 9; 7; 9];
A = [ 1 1 0 0 0 0 0 0 0;
1 0 1 0 0 0 0 0 0;
1 0 0 1 0 0 0 0 0;
0 1 1 0 0 0 0 0 0;
0 0 1 1 0 0 0 0 0;
0 1 0 1 0 0 0 0 0;
0 0 1 0 1 0 0 0 0;
0 0 0 1 1 0 0 0 0;
0 0 0 1 0 0 0 1 0;
0 0 0 1 0 0 1 0 0;
0 0 0 1 0 1 0 0 0;
0 1 0 0 0 0 1 0 0;
0 1 0 0 0 1 0 0 0;
0 0 0 0 1 0 1 0 0;
0 0 0 0 0 1 1 0 0;
0 0 0 0 1 0 0 1 0;
0 0 0 0 0 0 1 1 0;
0 0 0 0 0 1 0 1 0;
0 0 0 0 0 0 1 0 1;
0 0 0 0 0 1 0 0 1;
0 0 0 0 0 0 0 1 1];
b = ones(21, 1);
x = bintprog(f,-A,-b)
y = find(x) % номера вершин
Решение:
x =
y =
Таким образом, V* = {2, 3,4, 6, 7, 8}, т.е. в минимальное покрытие входят вершины с номерами 2, 3,4, 6, 7, 8,
Задача 7
|
|
|


