 |
Диагностическая контрольная работа
|
|
|
|
Правила раскрытия неопределенностей по правилу Лопиталя
1. Неопределенности вида  .
.
Раскрываются непосредственно с помощью правила Лопиталя.
2. Неопределенность вида  .
.
Для раскрытия неопределенности вида  , необходимо преобразовать соответствующее произведение
, необходимо преобразовать соответствующее произведение  , где
, где  ,
,  в частное:
в частное:  (вид
(вид 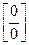 ) или
) или 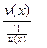 (вид
(вид  ).
).
3. Неопределенность вида 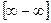 .
.
Для раскрытия неопределенности вида 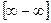 необходимо преобразовать соответствующую разность
необходимо преобразовать соответствующую разность  , где
, где  ,
,  , в произведение
, в произведение  и раскрыть сначала неопределенность
и раскрыть сначала неопределенность  . Если
. Если  , то выражение следует привести к виду
, то выражение следует привести к виду  (вид
(вид  ).
).
4. Неопределенности вида  .
.
Такого рода неопределенности раскрываются с помощью предварительного логарифмирования и нахождение предела степени  . Эти неопределенности сводятся к случаю неопределенности
. Эти неопределенности сводятся к случаю неопределенности  , при этом используется тождество
, при этом используется тождество
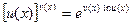 .
.
Задачи
Задача 1. Вычислить  .
.
Решение


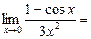


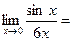


 .
.
При вычислении данного предела трижды применяли правило Лопиталя.
Ответ:  .
.
Задача 2. Вычислить  .
.
Решение


 .
.
При решении данной задачи дважды применяли правило Лопиталя.
Ответ:  .
.
Задача 3. Вычислить  .
.
Решение
В условии задачи подчеркнуто, что 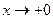 . Это указание является существенным, потому что при
. Это указание является существенным, потому что при  , так же, как и при
, так же, как и при  ,
, 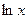 не существует, так как отрицательные числа логарифмов не имеют.
не существует, так как отрицательные числа логарифмов не имеют.
 .
.
При применении правила Лопиталя заменяется отношение функций отношением их производных.
Ответ: 0.
Задача 4. Вычислить  .
.
Решение





 .
.
Ответ:  .
.
Задача 5. Вычислить  .
.
Решение

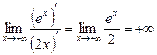
При решении данной задачи дважды применяли правило Лопиталя.
Ответ:  .
.
Задача 6. Вычислить  .
.
Решение
 .
.
Получили неопределенность 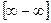 . По правилу 3 преобразуем выражение, стоящее под знаком предела к виду
. По правилу 3 преобразуем выражение, стоящее под знаком предела к виду  , путем приведения к общему знаменателю:
, путем приведения к общему знаменателю:
|
|
|





 .
.
Чтобы раскрыть неопределенность  , дважды применяли правило Лопиталя.
, дважды применяли правило Лопиталя.
Ответ:  .
.
Задача 7. Вычислить  .
.
Решение
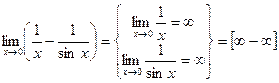 .
.
Получили неопределенность 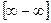 . По правилу 3 раскроем эту неопределенность, приводя ее к виду
. По правилу 3 раскроем эту неопределенность, приводя ее к виду 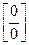 путем приведения к общему знаменателю:
путем приведения к общему знаменателю:



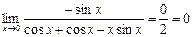 .
.
Чтобы раскрыть неопределенность 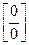 , дважды применяли правило Лопиталя.
, дважды применяли правило Лопиталя.
Ответ: 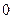 .
.
Задача 8. Вычислить  .
.
Решение

Получили неопределенность  . По правилу 2 преобразуем выражение, стоящее под знаком предела к виду
. По правилу 2 преобразуем выражение, стоящее под знаком предела к виду  :
:

 .
.
Ответ: 0
Задача 9. Вычислить  .
.
Решение
 .
.
Получили неопределенность  . По правилу 2 преобразуем выражение, стоящее под знаком предела к виду
. По правилу 2 преобразуем выражение, стоящее под знаком предела к виду  :
:
 .
.
Неопределенность  раскрыли, применяя правило Лопиталя.
раскрыли, применяя правило Лопиталя.
Ответ: 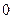 .
.
Задача 10. Вычислить  .
.
Решение
 .
.
Получили неопределенность  . На основании правила 4 воспользуемся тождеством
. На основании правила 4 воспользуемся тождеством 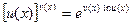 .
.

 .
.
Ответ: 1.
Задача 11. Вычислить  .
.
Решение
 . Получили неопределенность
. Получили неопределенность  . По правилу 4 воспользуемся тождеством
. По правилу 4 воспользуемся тождеством
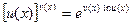 .
.
 .
.
Вычислим отдельно предел степени:




 ,
,
тогда  .
.
Ответ: 1.
Задача 12. Вычислить  .
.
Решение
 .
.
Получили неопределенность  . По правилу 4, принимая во внимание тождество
. По правилу 4, принимая во внимание тождество 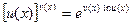 , находим:
, находим:
 .
.
Вычислим отдельно предел степени:






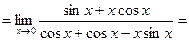
 .
.
Следовательно,  .
.
При нахождении предела степени трижды воспользовались правилом Лопиталя.
Ответ: 1.
Задача 13. Вычислить  .
.
Решение
 .
.
Получили неопределенность  . По правилу 4, учитывая тождество
. По правилу 4, учитывая тождество 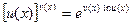 , находим:
, находим:
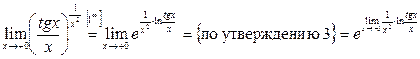 .
.
Отдельно вычислим предел степени:
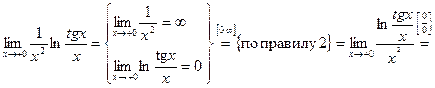


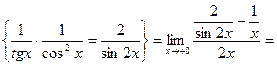




 .
.
Итак,  .
.
Правилом Лопиталя воспользовались четырежды при нахождении предела степени.
Ответ:  .
.
Задача 14. Вычислить  .
.
Решение
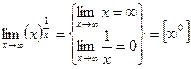 .
.
Получили неопределенность  . По правилу 4, применяя тождество
. По правилу 4, применяя тождество 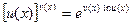 , раскроем эту неопределенность:
, раскроем эту неопределенность:
 .
.
Отдельно вычислим предел степени:


 .
.
Подставляя результат, получим:
 .
.
Ответ: 1.
Задача 15. Вычислить  .
.
Решение
 .
.
Получили неопределенность  . По правилу 4, принимая во внимание тождество
. По правилу 4, принимая во внимание тождество 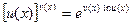 , находим:
, находим:
|
|
|
 .
.
Вычислим предел степени:
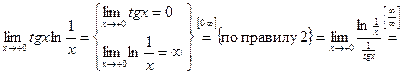



Последнюю неопределенность 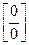 раскрыли с помощью первого замечательного предела. Тогда
раскрыли с помощью первого замечательного предела. Тогда  .
.
Ответ: 1.
Правило Лопиталя является эффективным приемом раскрытия неопределенностей, но не универсальным.
Задача 16. Вычислить  .
.
Решение
 .
.
При  функция
функция  не имеет предела, поэтому правило Лопиталя здесь неприменимо. Предел можно найти непосредственно:
не имеет предела, поэтому правило Лопиталя здесь неприменимо. Предел можно найти непосредственно:
 . Функция
. Функция  ограничена, так как
ограничена, так как  при любом
при любом 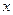 .А величина
.А величина 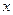 - бесконечно большая при
- бесконечно большая при  . Тогда по свойству: отношение ограниченной функции к бесконечно большой есть функция бесконечно малая
. Тогда по свойству: отношение ограниченной функции к бесконечно большой есть функция бесконечно малая 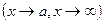 , имеем
, имеем  .
.
Ответ: 1.
Задача 17. Вычислить  .
.
Решение
 .
.
При  функция
функция  не имеет предела, поэтому правило Лопиталя неприменимо. Предел можно найти используя известный прием:
не имеет предела, поэтому правило Лопиталя неприменимо. Предел можно найти используя известный прием:
 . Функция
. Функция  ограничена, так как
ограничена, так как  при любом
при любом 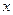 . А величина
. А величина 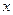 - бесконечно большая при
- бесконечно большая при  . Тогда по свойству: отношение ограниченной функции к бесконечно большой есть функция бесконечно малая
. Тогда по свойству: отношение ограниченной функции к бесконечно большой есть функция бесконечно малая 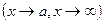 , имеем
, имеем  .
.
Ответ: 1.
Диагностическая контрольная работа
Вариант 1
Вычислить:
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4);
; 4); 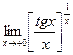 .
.
Вариант 2
Вычислить:
1)  ; 2)
; 2) 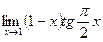 ; 3)
; 3) 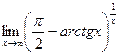 ; 4)
; 4)  .
.
Вариант 3
Вычислить:
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ;
;
Вариант 4
Вычислить:
1)  ; 2)
; 2)  ; 3)
; 3) 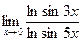 ; 4)
; 4)  .
.
Вариант 5
Вычислить:
1)  ; 2)
; 2)  ; 3)
; 3) 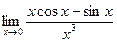 ; 4)
; 4)  .
.
Вариант 6
Вычислить:
1)  ; 2)
; 2) 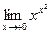 ; 3)
; 3)  ; 4)
; 4)  .
.
Домашнее задание
1. Теория: «Первый и второй замечательные пределы. Эквивалентные бесконечно малые».
2. Берман. Г.Н. Сборник задач по курсу математического анализа. №№ 383, 385, 391, 397, 399, 400.
|
|
|


