 |
Глава 5. Биматричные игры.
|
|
|
|
Игры с ненулевой суммой.
До сих пор рассматривались игры, в которых интересы игроков были прямо противоположны. В игре с ненулевой суммой интересы игроков хотя и не совпадают, о уже необязательно являются противоположными. Поэтому поведение игроков становится более разнообразным. В игре с ненулевой суммой становится желательным как-то координировать свои действия с партнером или каким-то способом влиять на его действия.
Игры с ненулевой суммой могут быть некооперативными и кооперативными. В некооперативных играх игроки принимают решения независимо друг от друга либо потому, что осуществление соглашения невозможно, либо потому, что оно запрещено правилами игры.
Пусть участник игры А может выбрать любую из стратегий А1, А2, …, Аm, а участник В – любую из стратегий В1, В2, …, Вn. Если игрок А выбрал стратегию Аi, а игрок В – стратегию Bk, то выигрыш игрока А будет равен числу аik, а выигрыш игрока В – числу bik,Таким образом, каждый из игроков получит свой приз. Выигрыши игроков А и В могут быть представлены двумя матрицами:
, 
Таким образом, имеем две матрицы: А – платежную матрицу игрока А; В – платежную матрицу игрока В. Поэтому такие игры получили название биматричных. Рассмотренные раньше матричные игры являются частным случаем биматричных, у которых aik=-bik.
Так же, как и для случая матричной игры, обозначим через 
вероятности с которыми игрок А использует в ходе игры свои чистые стратегии А1, А2, …, Аm. Для этих вероятностей выполняются условия
Аналогично, обозначим через 
, 
,…, 
вероятности, с которыми игрок B использует в ходе игры свои чистые стратегии 
, 
,…, 
. Для этих вероятностей выполняются условия:
Векторы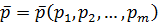 
и 
полностью определяют характер игры игроков A и B и называются смешанными стратегиями.
|
|
|
Можно показать, что для любой конечной некооперативной игры с ненулевой суммой всегда существует по крайней мере одна равновесная пара смешанных стратегий.
При использовании смешанных стратегий игра приобретает случайный характер, случайными становятся и величины выигрышей игроков. Поэтому выигрыши игроков A и B определяются математическими ожиданиями, рассчитываемыми по формулам:
Рассмотрим случай биматричной игры размера 
. В этом случае платежные матрицы игроков имеют вид:
вероятности 
а средние выигрыши вычисляются по формулам:
(6.1)
Пара чисел 
определяет равновесную ситуацию, если для любых p и q, удовлетворяющих условиям 
, 
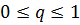, одновременно выполняются следующие неравенства:
(6.2)
Выполнение неравенств (6.2) равносильно выполнению следующих неравенств:
(6.3)
Четыре неравенства (6.3) позволяют провести поиск точки равновесия.
Перепишем формулы (6.1)для средних выигрышей в виде:
(6.4)
Положив в первой формуле (6.4) p=1 и p=0, получим:
Найдем соотношения для разностей:
где 
Перепишем эти соотношения в виде:
В случае, если пара (p,q) определяет точку равновесия, то в соответствии с (6.3) эти разности неотрицательны:
Сравнив это с предыдущей формулой, получим:
Аналогично для игрока B найдем:
где 
Таким образом, для того чтобы в биматричной игре:
пара (p, q) определяла равновесную ситуацию, необходимо и достаточно одновременное выполнение следующих неравенств:
(6.5)
где
(6.5)
Использование соотношений (6.5), (6.6) для решения задач рассмотрим на примерах.
Борьба за рынки.
Фирмы А и В производят однородный товар, который могут сбыть на одном из двух рынков. Фирма В является более состоятельной. Фирмы выбирают для борьбы один из рынков независимо друг от друга. Если фирмы выберут один и тот же рынок, то в конкурентной борьбе фирма А потерпит поражение. Если фирмы выберут разные рынки, то фирма А, не встречая противодействия, захватит выбранный рынок. Пусть платежные матрицы игроков имеют вид:
|
|
|
; 
.
Из этих матриц следует, что если фирмы выберут один и тот же рынок, то победа достанется фирме В. При выборе стратегий (А1,В1) выигрыш игрока В равен 5, а при выборе стратегий (А2,В2) его выигрыш равен 1. Это говорит о том, что первый рынок более выгоден, например удобно расположен, хорошо посещаем и т.д. Проигрыш игрока А при выборе стратегий (А1,В1) равен -10. А при выборе стратегий (А2,В2) – -1. Если фирмы выберут разные рынки, то при выборе стратегий (А1,В2) выигрыш игрока равен 2, а при выборе стратегий (А2,В1) его выигрыш равен 1. Здесь игрок А выигрывает больше на более выгодном рынке. Потери, которые несет при этом игрок В, оказываются прямо противоположными. Определить параметры равновесной ситуации.
По формулам (6.6) рассчитаем коэффициенты 
:
;
;
Подставив полученные значения в (6.5), получим
(6.7)
(6.8)
Рассмотрим сначала пару неравенств (6.7) для трех различных случаев: p=1, p=0, 0<p<1.
Для первого случая p=1получим:
Из второго неравенства находим:
или 
(6.9)
Для второго случая p=0 и
Из первого неравенства находим
или 
(6.10)
Для третьего случая 0<p<1 получим
Отсюда находим 
и 
. Выполнение этих двух неравенств одновременно возможно лишь при
(6.11)
Полученные результаты изображены на рис. 6.1.
Рис. 6.1
На рис. 6.1 выделен единичный квадрат, соответствующий неравенствам
Для первого случая p=1 имеем . На рис. 6.1 это луч, идущий из точки с координатами 
вниз. Для второго случая p=0 и . На рис. 6.1 это луч, идущий из точки с координатами 
вверх. Для третьего случая 0<p<1 получили . Это горизонтальный отрезок на интервале 0<p<1.
Получили зигзаг, выделенный полужирной линией. Нас интересует та часть зигзага, которая попала в выделенный единичный квадрат.
Рассмотрим теперь пару неравенств (6.8) для трех различных случаев q=1, q=0, 0<q<1.
Для первого случая q=1 найдем
Из второго неравенства получим 
или 
.
Для второго случая q=0 и 
, а для третьего случая 0<q<1 имеем 
.
Полученные результаты изображены на рис 6.2. Так же, как и в предыдущем случае, получили зигзаг, выделенный полужирной линией.
Результаты объединения рис. 6.1, 6.2 представлены на рис. 6.3.
|
|
|
Рис. 6.2 Рис. 6.3
Точкой равновесия является общая точка построенных зигзагов. Ее координаты равны 
. Тогда смешанные стратегии игроков имеют вид
.
Средние выигрыши игроков определим по формулам (6.1):
Дилемма узников.
Пример: Два узника находятся в предварительном заключении по подозрению в совершении преступления. Каждый узник имеет по две стратегии: молчать (стратегия М) или говорить (стратегия Г). Стратегия М – узник не признается в преступлении, стратегия Г- узник сознается в совершенном преступлении совместно с товарищем.
Если ни тот ни другой из узников не сознается в преступлении, то их потери составят -1, т.е. 
Если и тот и другой узники сознаются в преступлении, то их потери составляют -6 т.е. 
Приведенные условия представлены матрицами А и В:
; 
.
Определить параметры равновесной ситуации.
По формулам (6.6) рассчитаем коэффициенты С, α, D, β:
;
;
Подставив полученные значения в (6.5), получим:
(6.12)
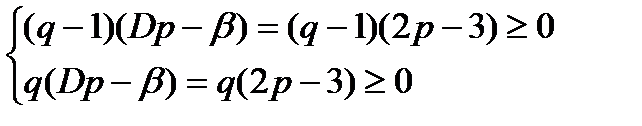(6.13)
Рассмотрим сначала пару неравенств (6.12) для трех различных случаев; p= 1, р = 0, 0< p < 1.
Для первого случая р = 1 получим:
Из второго неравенства находим
2q-3≥0, 2q≥3 или 
(6.14)
Для второго случая p= 0 и
Из первого неравенства находим
или 
. (6.15)
Для третьего случая 0< p < 1 получим
Отсюда находим -2q+3≥0 и 2q-3≥0. Выполнение этих двух неравенств одновременно возможно лишь при
(6.16)
Полученные результаты изображены на рис. 6.4.
Рис. 6.4
На рисунке 6.4 выделен единичный квадрат, соответствующий неравенствам
0< p < 1 и 0< q < 1.
Для первого случая р = 1 имеем 
. На рис.6.4 это луч, идущий из точки с координатами 
вверх.
Для второго случая р = 0 и . На рис.6.4 это луч, идущий из точки с координатами 
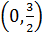вниз.
Для третьего случая 0< p < 1 получили . Этот горизонтальный отрезок на интервале 0 <p< 1, соединяющий точки с координатами и .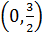
Получили зигзаг, выделенный полужирной линией. Нас интересует та часть зигзага, которая попала в выделенный единичный квадрат.
Рассмотрим теперь пару неравенств (6.13) для трёх различных случаев: q=1, q=0, 0 < q < 1.
|
|
|
Для первого случая q=1найдем
Из второго неравенства получим 
или 
.
Для второго случая 
и 
, а для третьего случая 0<q<1имеем 
.
Полученные результаты изображены на рис. 6.4. Так же, как и в предыдущем случае, получили зигзаг, выделенный полужирной линией.
Точкой равновесия является общая точка построенных зигзагов. Её координаты (0,0). Тогда смешанные стратегии игроков имеют вид
.
Средние выигрыши игроков вычисляются по формулам (6.1):
.
Это значит, что каждый игрок выбирает вторую смешанную стратегию (сознаться) и его потери составят -6. По условию задачи сговор (создание коалиции) между игроками запрещён. В противном случае игроки выбрали бы первую чистую стратегию (молчать), по которой каждый теряет -1.
Кооперативные игры.
Кооперативной игрой называется игра с ненулевой суммой, в которой игрокам разрешается обсуждать перед игрой свои стратегии и договариваться о совместных действиях, т.е. игроки могут образовывать коалиции.
Основная задача в кооперативной игре состоит в дележе общего выигрыша между членами коалиции.
Пусть выигрыши двух игроков определяются множеством S в пространстве переменных x и у, где х – выигрыш первого игрока, а у – выигрыш второго игрока (рис. 6.5).
Рис. 6.5
Множество S является выпуклым, замкнутым и ограниченным сверху. Точка Т с координатами хТ и уТ определяет величины выигрышей, которые игроки могут получить, не вступая в коалицию друг с другом. Эта точка называется точкой угрозы.
Парето-оптимальным множеством называется множество точек, образующих северо-восточную границу множества S (множество АВ на рис. 6.5).
Для этой области увеличение выигрыша одного игрока возможно только за счет уменьшения выигрыша другого.
Переговорным множеством называются точки Парето оптимального множества, координаты которых превышают хТ по оси х и уТ по оси у.
Иначе говоря, точки переговорного множества находятся выше и правее точки угрозы Т. Игрокам нет смысла договариваться относительно решений, не принадлежащих переговорному множеству.
Точкой решения Нэша называется точка, в которой достигается максимум 
, где 
и 
— превышения выигрышей каждого из игроков над платежами, которые могут быть получены без вступления в коалицию.
Если множество возможных платежей S выпукло, замкнуто и ограничено сверху, то точка Нэша существует и единственна.
Пример 6.1. Найти точку Нэша. Платежные матрицы в этой игре имеют вид
.
Определить параметры равновесной ситуации.
Решение. Средние выигрыши игроков А и В вычисляются по формулам (6.1):
(6.17)
Две эти функции заданы на единичном квадрате (рис. 6.6)
|
|
|
.
Рис. 6.6
Построим область, заполненную точками с координатами 
. Для определения первой границы этой области положим q = 0 и рассмотрим отрезок на оси Ор от нуля до единицы. При заданных условиях (6.17) приобретает вид:
(6.18)
Функция 
задана параметрически, где параметром является р. Умножив первое уравнение (6.18) на 2 и сложив уравнения системы (6.18), получим
.
Это уравнение прямой, т.е. граница искомой области является отрезком данной прямой (отрезок CF на рис. 6.7), причем точка 
соответствует 
, а точка 
— 
. Точно так же можно оказать, что остальные границы искомой области являются отрезками прямых.
Вторая граница. При и 
соотношения (6.17) приобретают вид:
При 
имеем 
, т.е. точку 
; при 
— 
, т.е. точку 
. Таким образом, искомым отрезком является отрезок LF.
Третья граница. При 
и :
При 
имеем 
, т.е. точку ; при - 
, т.е. точку 
. Искомым отрезком является отрезок CD.
Четвертая граница. При и 
:
При имеем 
, т.е. точку ; при — 
, т.е. точку 
. Искомым отрезком является отрезок LD.
Из сказанного следует, что областью, заполненной точками с координатами 
, является область внутри четырехугольника CDLF (рис. 6.7). Парето-оптимальным множеством является ломаная CDL.
Рис. 6.7
Координаты точки угрозы Т определяются путем подстановки в (6.17) координат точки равновесия биматричной игры. Эти координаты были найдены при решении примера 15.11: р* = 0, q* = 0.
Тогда
Таким образом, точкой угрозы является точка .
Точкой решения Нэша называется точка, в которой достигается максимум 
. Можно показать, что это точка . Ей соответствуют чистые стратегии обоих игроков (см. пункт «Третья граница»): , .
Все это означает, что потери узников составят -1, и стратегиями узников является «молчать», т.е. ни тот ни другой из узников не сознается в преступлении.
|
|
|
