 |
Экстремум функции двух переменных.
|
|
|
|
Функция нескольких переменных (ФНП).
Определение функции нескольких переменных ______________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
График функции 2-х переменных.____________
_________________________________________________________________________________________________________
Линия уровня_________________________
___________________________________
______________________________________________________________________
Простейшим примером функции нескольких переменных, используемой в экономике, является производственная функция.
Производственная функция – зависимость результатов производственной деятельности (выпуска продукции) от обусловивших его факторов – затрат ресурсов.
Производственная функция двух переменных вида 
называется функцией Кобба-Дугласа. Параметры α и β – частные эластичности выпуска продукции (постоянные величины) по отношению к переменным факторам х и у. График этой функции представляет собой некоторую поверхность трёхмерной системы координат, построение которой может вызвать определённые сложности. Но можно значительно упростить задачу, зафиксировав одну из переменных, как постоянную, придавая ей определённые значения.
Пример. Изменяя величину фонда заработной платы постройте производственную функцию 
, где 
- объем товарной продукции в стоимостном выражении, х - фонд заработной платы (млрд. руб.), у - стоимость основных фондов (млрд. руб.).
| |||||||
| |||||||
|
| |||||||
|
| |||||||
|
|
§ 2. Частные и полное приращения функции двух переменных. Частные производные функции двух переменных.
|
|
|
Пусть задана функция z = f (x, y). Так как х и у – независимые переменные, то одна из них может изменяться, а другая оставаться постоянной. Дадим независимой переменной х приращение 
, сохраняя значение у неизменным. Тогда z получит приращение, которое называют частным приращением z по x и обозначают:
Сформулировать самостоятельно частное приращение z по y ________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определение частной производной по х _____________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Частная производная по х обозначается одним из символов: 
; 
; 
; 
Аналогичным образом даётся следующее определение (самостоятельно)
Определение частной производной по y _____________________________________________
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Частная производная по у обозначается одним из символов: _______________________
Пример. Найти частные производные функции двух переменных 
по каждой из переменных: х и у.
Решение. Производную 
найдём, считая х переменной, а у постоянной величиной:
Производную 
найдём, считая у переменной, а х постоянной величиной:
Геометрический смысл частных производных функции двух переменных.
______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
|
|
|
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_________________________________________________________________________________________ __________________________________________________________________________________________________________________________________________________________________________________
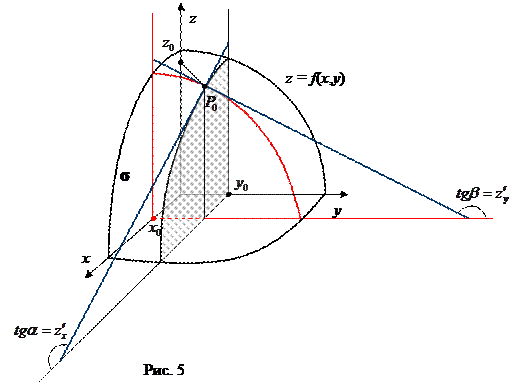
Частные производные высших порядков.
______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Схема формирования частных производных высших порядков функции двух переменных.
 |
Определение. Смешанными частными производными называют___________________________
_________________________________________________________________________________________________________________________________________________________________________________
Теорема (о смешанных производных) ______________________________________________
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Принимаем теорему без доказательств.
Пример. Найти частные производные второго порядка функции 
.
Решение. Производную найдём, считая х переменной, а у постоянной величиной:
Производную найдём, считая у переменной, а х постоянной величиной:
Вторые производные по х и по у будем искать, дифференцируя найденные производные первого порядка:
Мы убедились, что теорема выполняется:
Полный дифференциал функции.
По рис.4 _______________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________________
Определение функции, дифференцируемой в точке. _____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
|
|
|
(1)
___________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определение полного дифференциала. ____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
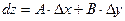(2)
Примем без доказательств, что если функция z = f (x,y) дифференцируема в точке M (x; y), то 
и 
. Приращения 
, 
. Тогда равенство (2) можно переписать, как
Приложение полного дифференциала к приближённым вычислениям.
Линеаризация функции в окрестности точки.
Постановка задачи и вывод формулы. ____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
___________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
___________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
___________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_________________________________________________________________________________________
___________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Пример. Вычислить приближенное значение функции 
в точке 
с помощью полного дифференциала, оценить абсолютную и относительную погрешность.
Решение. ______________________________________________________________________________
|
|
|
__________________________________________________________________________________________________________________________________________________________________________________
___________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_________________________________________________________________________________________
___________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Экстремум функции двух переменных.
Окрестность точки______________________________________
______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определение максимума функции двух переменных_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определение минимума функции двух переменных._________________ _______
_____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определение экстремума._______________________________________________________ _______________________________________________________________________________________
Теорема (необходимое условие экстремума)__________________________________________
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Принимаем без доказательств.
Необходимое условие экстремума не является достаточным (!)
Пример. Рассмотрим функцию 
(рис. 10).
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определение критической (стационарной) точки второго рода ____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Для ответа на вопрос, является ли точка области определения функции точкой экстремума, нужно использовать достаточное условие экстремума.
Теорема (достаточное условие экстремума)__________________________________________
_________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
|
|
|
Пример 1. Исследовать на экстремум функцию 
.
Решение.
1) Находим производные первого порядка.
2) Находим критические точки. Для этого решим систему уравнений:
Получаем две критические точки: __________________
3) Находим производные второго порядка:
4) Исследуем первую критическую точку:
Следовательно, ________________________________________________
5) Исследуем вторую критическую точку:
Следовательно, ________________________________________________
Пример 2. Исследовать на экстремум функцию 
.
Решение. (самостоятельно)
1) Находим производные первого порядка.
2) Находим критические точки. Для этого решим систему уравнений:
Получаем две критические точки: __________________
3) Находим производные второго порядка:
4) Исследуем первую критическую точку:
Следовательно, ________________________________________________
5) Исследуем вторую критическую точку:
Следовательно, ________________________________________________
|
|
|
