Получение временных характеристик динамических звеньев

Основы теории управления: практикум / В.Ю. Емельянов, А.Ю. Захаров, Е.А. Курилова, О.А. Мишина; под ред. В.Ю. Емельянова; Балт. гос. техн. ун-т; СПб., 2015. с.

 

Представлены материалы аудиторного и лабораторного практикумов, посвященных основам теории линейных непрерывных систем управления.

Содержит материалы девяти практических занятий, два домашних задания и описание семи лабораторных работ, выполняемых с помощью комплекса контрольно-обучающих программ.

Рассматриваются построение математических моделей динамических звеньев и систем управления, получение временных, частотных и логарифмических частотных характеристик, анализ устойчивости и качества, некоторые задачи параметрического синтеза линейных непрерывных систем управления.

Представлены основные сведения из теории, большое количество примеров, практические рекомендации по выполнению лабораторных работ, наборы контрольных вопросов и задач для самостоятельного решения, наборы индивидуальных вариантов домашних заданий, перечень рекомендуемой литературы.

Предназначено для студентов укрупненных групп направлений и специальностей (УГСН) 160000, 170000, 200000, 210000, 230000, изучающих дисциплины «Основы теории управления», «Управление в технических системах», «Радиоавтоматика» и др.

 

Рецензент: канд. физ.-мат. наук, доц. кафедры БГТУ «Прикладная механика, автоматика и управление» И.Л. Коробова

 

Оглавление

АУДИТОРНЫЙ ПРАКТИКУМ…………………………………………….5

Практическое занятие №1. Составление математических моделей динамических звеньев…………………………………………………………5

Практическое занятии №2. Получение временных характеристик динамических звеньев………………………………………………………..14

Практическое занятие №3. Получение частотных характеристик динамических звеньев……………………………………………………..…25

Практическое занятие №4. Логарифмические частотные характеристики динамических звеньев и систем…………………..………….....38

Практическое занятие №5. Преобразование структурных схем. Передаточные функции замкнутых систем…………………………………..51

Практическое занятие №6. Анализ устойчивости линейных стационарных систем (алгебраические методы)…………………………….…61

Практическое занятие №7. Анализ устойчивости линейных стационарных систем (частотные методы)……………………………………...70

Практическое занятие №8. Оценка качества систем управления.…82

Практическое занятие №9. Примеры синтеза систем управления...90

ДОМАШНИИ ЗАДАНИЯ……………………………… ………………….99

Домашнее задание№1. Составление математической модели и получение характеристик динамического звена………….………………….99

Домашнее задание №2. Анализ линейной системы управления……102

ЛАБОРАТОРНЫЙ ПРАКТИКУМ……………………………………..…104

Лабораторная работа №1. Построение амплитудно-фазовых частотных характеристик…………………………………………………………104

Лабораторная работа №2. Определение фазо-частотных характеристик………………………………………….…………………….…………108

Лабораторная работа №3. Построение асимптотических лагарифмических амплитудных характеристик……………………………………110

Лабораторная работа №4. Характеристики типовых динамических звеньев……………………………………………………………………….119

Лабораторная работа №5. Логарифмические и амплитудно-фазовые частотные характеристики………………………………………….……129

Лабораторная работа №6. Оценка устойчивости по логарифмическим характеристикам………………………………….……………….…132

Лабораторная работа №7. Характеристики типовых динамических звеньев………………………………………………………………………..147

Библиографический список……………………………………………….153

Приложение 1………………………………………………………………..154

 

АУДИТОРНЫЙ ПРАКТИКУМ

Практическое занятие 1

Составление математических моделей динамических звеньев

При составлении математической модели системы ее разбивают на динамические звенья. Далее составляют математические модели динамических звеньев с использованием сведений из соответствующей их физической природе науки. После этого динамические звенья объединяют в модель системы, учитывая их взаимное влияние.

Динамическое звено – это устройство любой физической природы и любого конструктивного исполнения, описываемое дифференциальным уравнением определенного вида. То есть главное здесь – конкретное математическое описание. Именно с математическими моделями работает теория управления. Поэтому математическая модель звена или системы должна правильно отображать их свойства, существенные с точки зрения решаемой задачи.

Электрическая схема, электрический двигатель, кастрюля с супом, летательный аппарат, студенческая аудитория и пр. при определенных допущениях, определяемых условиями задачи, оказываются одним и тем же динамическим звеном, то есть демонстрируют аналогичные динамические свойства. Формально это определяется тем, что для всех этих объектов может быть получено одно и то же дифференциальное уравнение (различие может быть только в численных значениях коэффициентов).

Для одного и того же реального объекта могут быть составлены разные модели динамического звена – тоже в зависимости от условий задачи и допущений.

Фундаментальным свойством динамического звена является направленность действия. То есть с формальной точки зрения динамическое звено преобразует свои входные сигналы в выходные и ни в коем случае не наоборот.

Под входными сигналами понимают конкретные физические параметры, характеризующие воздействие на динамическое звено предшествующих по структурной схеме системы звеньев или внешней среды. Под выходными сигналами понимают конкретные физические параметры, характеризующие воздействие рассматриваемого звена на последующие по структурной схеме системы звенья.

В соответствии со сказанным для динамического звена используются условные обозначения, показанные на рис. 1: а) звено с одним входом и одним выходом; б) звено с тремя входами и двумя выходами.

Рис. 1.

Свойство направленности действия можно сформулировать несколько иначе: характеристики преобразования звеном входных сигналов не зависят от характеристик последующих звеньев, от их наличия или отсутствия.

Разбивать систему на динамические звенья необходимо так, чтобы каждое звено обладало свойством направленности действия. Поэтому часто структура модели системы отличается от ее функциональной схемы, отражающей состав реальных элементов. Если отдельные элементы системы не обладают рассматриваемым свойством, они могут разбиваться на динамические звенья или объединяться в них.

Пример 1.1.

Составить математическую модель динамического звена для четырехполюсника, схема которого представлена на рис. 2а. В качестве входного и выходного сигналов рассматривать напряжения на контактах четырехполюсника.

Рис. 2.

Рассмотрим вопрос о наличии у рассматриваемого звена свойства направленности действия. Как известно из электротехники, последующее устройство выполняет для четырехполюсника роль нагрузки (рис. 2б). Сопротивление нагрузки влияет на выходное напряжение любого электрического устройства. Пренебречь этим влиянием можно, если сопротивление нагрузки достаточно велико. В этом и последующих примерах принимается, что условия наличия свойства направленности действия имеют место.

Рис. 3.

Воспользуемся законами Ома, Кирхгофа и известным соотношением между напряжением и током конденсатора и составим уравнения, описывающие процессы в четырехполюснике (рис. 3):

u ₁- u_R - u_C= 0,

u_R=Ri,

,

u_C=u ₂.

Полученная система уравнений приемлема с точки зрения прикладной науки, соответствующей физической природе рассматриваемого устройства, но не может рассматриваться как модель динамического звена. Дело в том, что с точки зрения теории управления физическая природа динамического звена не имеет значения. Учитываются только его динамические свойства, отраженные абстрактной математической моделью. Поэтому к записи моделей динамических звеньев предъявляются совершенно определенные жесткие требования:

1. В дифференциальном уравнении звена должны присутствовать только входные и выходной сигнал (при наличии нескольких выходных сигналов для каждого составляется отдельное уравнение).

2. В левой части уравнения должны присутствовать только выходной сигнал и его производные, в правой – входные сигналы и их производные.

3. В левой части уравнения выходной сигнал должен иметь коэффициент единица. Если присутствуют только производные выходного сигнала, коэффициент единица должен быть при низшей производной.

Отметим, что к дифференциальному уравнению системы предъявляются те же требования, за исключением третьего.

Последовательными подстановками исключим из полученной системы уравнений все переменные, кроме входного u ₁ и выходного u ₂ сигналов (выполним первое требование):

.

Теперь выполним второе требование:

.

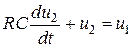Третье требование оказалось также выполненным.

Теперь можно перейти к стандартной абстрактной форме записи модели динамического звена:

, (1.1)

где T=RC, k= 1.

Структура полученного уравнения отражает наличие у динамического звена тех или иных свойств. Величины коэффициентов – глубину этих свойств. Поэтому коэффициенты уравнений динамических звеньев имеют различный смысл, названия и обозначения. Коэффициенты при производных – постоянные времени, коэффициенты при входных сигналах в правой части – коэффициенты передачи. При введении постоянных времени следует заботиться об обеспечении одинаковой размерности у всех слагаемых в уравнении (первая производная имеет размерность с^-1, вторая – с^-2 и так далее; постоянная времени имеет размерность «с»). При появлении в уравнении производных второго и более высокого порядка коэффициенты при них должны содержать произведения постоянных времени.

Пример 1.2.

Составить математическую модель динамического звена (рис. 4).

Рис. 4.

В соответствии со вторым законом Ньютона сила F уравновешивается силой динамического сопротивления жидкости движению поршня и силой упругости пружины:

F=F_д+F_у ,

где и .

В результате:

.

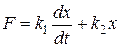Перенесем слагаемые, содержащие выходной сигнал и его производную, в левую часть уравнения; входной сигнал – в правую часть:

.

Делением на k ₂ приведем к единице коэффициент при выходном сигнале:

.

После выполнения всех требований к записи уравнения представим его в стандартной форме:

,

где , .

Нетрудно видеть, что в двух рассмотренных примерах получено одно и то же по структуре дифференциальное уравнение. Таким образом, с точки зрения теории управления два рассмотренных устройства различной физической природы между собой не различаются. Оба они будут рассматриваться как апериодическое звено 1-го порядка.

Вместе с дифференциальным уравнением и даже более часто в классической теории управления используется другая форма математического описания динамического звена или системы – передаточная функция.

Передаточная функция звена или системы – это отношение изображений по Лапласу выходного и входного сигналов при нулевых начальных условиях и отсутствии других входных сигналов:

.

В соответствии с этим определением можно сделать вывод, что при наличии нескольких входных и выходных сигналов для рассматриваемого звена или системы должен рассматриваться набор передаточных функций – от каждого входа к каждому выходу. Так для звена с тремя входами и двумя выходами (рис. 1б) должны быть получены шесть передаточных функций.

Переход от дифференциального уравнения звена к передаточной функции основан на свойстве линейности преобразования Лапласа и теореме дифференцирования . Отметим, что содержащееся в определении передаточной функции требование учета нулевых начальных условий упрощает выражение для изображения производной: и в общем случае . Оператор Лапласа при нулевых начальных условиях приобретает смысл символа дифференцирования.

Получим передаточную функцию апериодического звена 1-го порядка. С учетом указанных выше свойств перейдем от дифференциального уравнения звена (1.1) к операторному уравнению для изображений сигналов:

.

Полученное уравнение является алгебраическим и допускает следующее преобразование:

.

Разделив левую и правую части на X ₁(s) и сомножитель при X ₂(s), получим искомую передаточную функцию:

.

Уже этот простой пример демонстрирует взаимно однозначное соответствие между записанным строго в соответствии с правилами дифференциальным уравнением и передаточной функцией звена или системы – левая часть уравнения взаимно однозначно соответствует знаменателю передаточной функции, правая – числителю. Но это имеет место только при нулевых начальных условиях в соответствии с определением передаточной функции.

Пример 1.3.

Задано дифференциальное уравнение динамического звена:

.

Получить передаточную функцию.

Запишем передаточную функцию, учитывая отмеченное выше взаимно однозначное соответствие:

.

Аналогично выполняется и обратный переход.

Пример 1.4.

Составить математическую модель динамического звена (рис. 5).

Рис. 5.

Основой моделируемого устройства здесь является операционный усилитель, для которого может использоваться приближенное соотношение:

,

где Z_вх и Z_ос – комплексные сопротивления входной цепи и цепи обратной связи операционного усилителя (рис. 6).

Рис. 6.

Комплексные сопротивления Z_вх и Z_ос находят с учетом правил для последовательного и параллельного соединения элементов и выражений для комплексных сопротивлений реактивных элементов.

Известно, что для общего случая токов произвольной формы комплексные сопротивления конденсатора и катушки индуктивности определяются выражениями:

и .

В результате для рассматриваемого примера получим:

и .

Теперь можем непосредственно получить искомую передаточную функцию:

,

и в общей форме опять получаем апериодическое звено первого порядка:

,

где , .

Следует отметить удобный способ получения передаточных функций четырехполюсников, если в качестве входного и выходного сигналов рассматриваются напряжения. Он основан на уравнении делителя напряжения (рис. 7) при достаточно большом сопротивлении нагрузки:

.

Рис. 7.

 

Вернемся к примеру 1.1. Для него U_вх=U ₁, U_вых=U ₂, Z ₁= R и 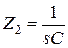. В результате получим:

,

где T=RC, k= 1. Результат полностью совпадает с полученным выше.

Использование рассмотренного способа возможно только, если схема четырехполюсника допускает выделение двух участков, то есть приводится к схеме простейшего делителя напряжения.

Теперь рассмотрим два примера, показывающих важность правильного выбора входных и выходных сигналов или правильного учета заданного их выбора.

Пример 1.5.

Составить математическую модель динамического звена (рис. 2а), рассматривая в качестве выходного сигнала ток через конденсатор: x ₁= u ₁, x ₂= i.

Воспользуемся уравнениями из примера 1.1:

u ₁- u_R - u_C= 0,

u_R=Ri,

.

Подставим u_R в первое уравнение и выразим из него u_C:

u_C=u ₁- Ri.

Теперь подставим u_C в третье уравнение:

.

Выполним правила записи уравнения динамического звена:

,

или

, ,

где T=RC, k=C.

Теперь наш четырехполюсник – другое динамическое звено – дифференцирующее звено с замедлением.

Пример 1.6.

Составить математическую модель динамического звена (рис. 2а), рассматривая ток в качестве входного сигнала: x ₁= i, x ₂= u ₂.

Здесь достаточно двух уравнений:

,

,

из которых получим:

, ;

,

,

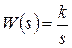где . Это идеальное интегрирующее звено.

Таким образом, даже для простейшего объекта в зависимости от выбора входного и выходного сигналов могут быть получены принципиально разные модели, отражающие иногда противоположные динамические свойства.

 

Контрольные вопросы и задачи для самостоятельной работы

1. В чем состоит смысл понятий «динамическое звено» и «направленность действия»?

2. Перечислите правила записи уравнения динамического звена.

3. При каких условиях определяется передаточная функция?

4. Составьте уравнение динамического звена по передаточной функции:

.

5. Составьте дифференциальные уравнения и передаточные функции динамических звеньев, представленных на рис. 8.

Рис. 8.

6. Составьте модель динамического звена (рис. 2б) с учетом конечной нагрузки .

Изменятся ли тип звена и значения его параметров по сравнению с примером 1.1? Каков будет характер изменений?

Практическое занятие 2

Получение временных характеристик динамических звеньев

Переходная характеристика (переходная функция) – это реакция звена или системы на входной сигнал в виде единичной ступенчатой функции (рис. 9).

Рис. 9.

Рассмотрим наиболее удобные методы получения переходной характеристики.

Классический метод – путем решения дифференциального уравнения звена или системы.

Пример 2.1.

Найти переходную характеристику апериодического звена 1-го порядка.

Дифференциальное уравнение звена: .

В соответствии с определением переходной характеристики замене абстрактного входного сигнала x ₁ на единичную ступенчатую функцию будет соответствовать замена x ₂ на переходную функцию:

.

Такая запись предусматривает решение дифференциального уравнения

на интервале времени .

Решение линейного неоднородного дифференциального уравнения ищут в виде суммы двух составляющих:

,

где h ₀ – общее решение, h* –частное решение. В теории управления общее решение называют переходной составляющей, частное решение – вынужденной составляющей:

.

Переходную составляющую находят как решение однородного дифференциального уравнения:

в форме суммы экспонент с произвольными коэффициентами. В показателях степени экспонент используются корни характеристического уравнения.

Например, если все корни вещественные, причем кратные корни отсутствуют, переходная составляющая имеет вид:

.

В рассматриваемом примере характеристическое уравнение имеет вид:

и имеет один корень .

В результате получим выражение для переходной составляющей:

.

Вынужденную составляющую находят в форме, соответствующей правой части. Если правая часть – константа, вынужденная составляющая – также константа, и для ее нахождения достаточно в уравнении положить производные равными нулю. В результате: .

Результирующее полное решение уравнения:

.

Произвольные константы находят через начальные условия, которые для временных характеристик динамических звеньев принимаются равными нулю.

Найдем C ₁: , C ₁= -k.

В результате получена переходная характеристика:

.

Необходимо учесть, что в практических задачах переходные характеристики могут рассматриваться на различных временных интервалах. Для того, чтобы избавиться от необходимости отдельно указывать эту дополнительную информацию, выражения для переходных характеристик домножают на единичную ступенчатую функцию с соответствующим аргументом. Для рассматриваемого примера результат должен быть представлен в следующем виде:

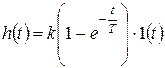. (2.1)

График переходной характеристики показан на рис. 10а.

Полученная характеристика показывает, что апериодическое звено 1-го порядка воспроизводит входной сигнал. Но это происходит с замедлением – по окончании переходного процесса. То есть данное звено характеризуется инерционностью.

Рис. 10.

Отметим дополнительно, что при наличии производных в правой части уравнения может возникнуть необходимость учитывать скачкообразное изменение начальных условий. Поэтому с учетом наличия других методов классический можно рекомендовать для решения уравнений без производных в правой части.

На основе полученной характеристики полезно проанализировать влияние параметров звена на его динамические свойства. Определим крутизну графика переходной характеристики при t =0:

,

при t =0 получаем 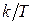. Отсюда можно сделать вывод о расположении касательной к графику h (t) в момент начала переходного процесса, отображенный на рис. 10б и позволяющий прогнозировать влияние величины постоянной времени на характер переходного процесса.

Таким образом, при увеличении значения постоянной времени переходный процесс замедляется. Постоянная времени характеризует инерционность динамического звена.

На рис. 10в отображено влияние на процесс в звене коэффициента передачи.

Операторный метод – на основе передаточной функции звена.

Воспользуемся определениями передаточной функции и переходной характеристики с учетом известного изображения по Лапласу единичной ступенчатой функции :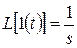

.

Следовательно, при заданной передаточной функции изображение переходной характеристики можно найти по формуле:

.

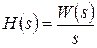После этого переходная характеристика может быть найдена путем перехода от изображения к оригиналу одним из следующих способов:

- непосредственно с помощью таблицы изображений (Приложение 1) – в простейших случаях;

- разложением H (s) на сумму табличных изображений;

- с помощью теорем разложения [9].

Пример 2.2.

Найти переходную характеристику дифференцирующего звена с замедлением. Передаточная функция звена .

Найдем изображение переходной характеристики:

и воспользуемся строкой 3 из таблицы изображений (Приложение 1).

Преобразуем имеющееся изображение к табличному виду:

и с учетом линейности преобразования Лапласа получим искомую характеристику:

.

График переходной характеристики показан на рис. 11. Выполнив анализ, аналогичный примеру 2.1, определим расположение касательной к характеристике в начальный момент времени.

Рис. 11.

Пример 2.3.

Найти переходную характеристику интегрирующего звена с замедлением. Передаточная функция звена .

Найдем изображение переходной характеристики:

.

Разложим изображение на сумму:

.

Приведя разложение к общему знаменателю

и приравняв числители полученного и исходного выражений, получим уравнения для коэффициентов:

AT+C= 0,

A+BT= 0,

B=k,

откуда A= -kT, .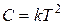

Воспользовавшись таблицей изображений с учетом линейности преобразования Лапласа запишем искомый оригинал как сумму:

.

Для построения характеристики сначала рассмотрим графики двух слагаемых полученного выражения (рис. 12а), которые помогают получить итоговый график (рис. 12б).

Рис. 12.

В наиболее сложных случаях для нахождения оригинала по изображению используют теоремы разложения.

Пример 2.4.

Найти переходную характеристику колебательного звена.

Передаточная функция звена , причем , что обеспечивает комплексные корни знаменателя.

Найдем изображение переходной характеристики:

.

Воспользуемся одной из теорем разложения: для изображения вида оригинал имеет форму , где s_i – корни полинома Y ₃.

Корни полинома Y ₃ в рассматриваемом примере имеют вид: .

Производная Y ₃: .

Перейдем к оригиналу:

.

Теперь учтем теорему Эйлера и соответственно , а также соотношения: и .

Все это позволяет ввести в рассмотрение угол , причем принять и . С учетом этих соотношений продолжим преобразование выражения для переходной характеристики:

и окончательно

.

График характеристики отображает затухающий колебательный процесс (рис. 13). Учитывая , отметим, что амплитуда колебаний убывает в зависимости от времени по экспоненциальному закону (огибающие колебаний показаны пунктирными линиями).

Рис. 13.

Весовая характеристика (весовая функция, функция веса) – это реакция звена или системы на входной сигнал в виде 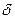– функции (рис. 14).

Вспомним основные свойства функции (функции Дирака):

, , .

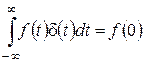Рассмотрим наиболее удобные способы (методы) получения весовой характеристики.

Рис. 14.

Операторный метод.

Воспользуемся определениями передаточной функции и весовой характеристики с учетом известного изображения по Лапласу 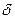– функции :

.

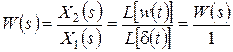Следовательно, передаточная функция является изображением по Лапласу функции веса.

Пример 2.5.

Найти весовую характеристику апериодического звена 1-го порядка.

Преобразуем передаточную функцию звена к табличному виду

и запишем результат:

.

График весовой характеристики показан на рис. 15.

Рис. 15.

Получение весовой функции дифференцированием переходной характеристики.

Следствием полученного выше соотношения является следующая связь между весовой и переходной функциями:

.

Вернемся к последнему примеру.

Переходная характеристика апериодического звена 1-го порядка была получена выше в виде (2.1). Продифференцируем ее:

.

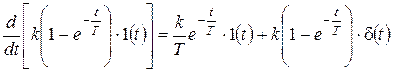С учетом тождественного равенства нулю функции при всех упростим полученное выражение:

.

 

Контрольные вопросы и задачи для самостоятельной работы

1. Как связаны между собой:

- передаточная и переходная функции?

- переходная и весовая функции?

- весовая и передаточная функции?

2. Как скажется повышение инерционности дифференцирующего звена с замедлением на его реакции на входной сигнал (на примере переходной характеристики)?

3. Проанализируйте влияние параметров колебательного звена на его динамические свойства (на примере переходной характеристики).

4. Получите, используя в каждом случае не менее двух способов, аналитические выражения и графики временных характеристик для динамических звеньев:

а) , T ₁< T ₂; б) , T ₁> T ₂;

в) ; г) .

Проанализируйте влияние параметров рассмотренных звеньев на их динамические свойства.

5. С использованием теоремы дифференцирования получите на основе переходной характеристики апериодического звена 1-го порядка переходные характеристики и функции веса следующих звеньев:

; б) .

Практическое занятие 3

12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: