 |
Раздел 1. Электростатика. Электрическая емкость.
|
|
|
|
1. заряд Q равномерно распределён по объему шара радиуса R. Полагая диэлектрическую проницаемость всюду равную 1, определить зависимость поля E и потенциала φ от расстояния r до центра шара (внутри и вне шара) и построить соответствующие графики E(r) и φ(r)(0<=r<=∞). Вычислить E и φ в центре и на поверхности шара. Выполнить аналогичные задания для случаев металлической сферы, несущей заряд Q. 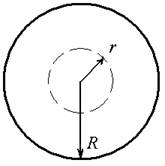
| Q,R |
| E(r), φ(r)-? |
Решение:
Поле такой системы будет сферически симметрично, т.к. сфера заряжена однородно, поэтому мы и можем говорить о функциях поля и потенциала в зависимости от расстояния до центра. Тогда применим теорему Гаусса:

 , здесь q – заряд внутри выбранной замкнутой поверхности S. Т.к. шар заряжен однородно, то объемная плотность заряда в сфере постоянна
, здесь q – заряд внутри выбранной замкнутой поверхности S. Т.к. шар заряжен однородно, то объемная плотность заряда в сфере постоянна 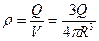 , тогда можно подставить это в теорему Гаусса(сначала рассмотрим случай r<R):
, тогда можно подставить это в теорему Гаусса(сначала рассмотрим случай r<R):  , а из соображений постоянства поля на одном и том же расстоянии до центра и того что оно перпендикулярно поверхности сферы в любой точке следует, что E -константа в интеграле справа и знак вектора можно убрать -
, а из соображений постоянства поля на одном и том же расстоянии до центра и того что оно перпендикулярно поверхности сферы в любой точке следует, что E -константа в интеграле справа и знак вектора можно убрать - 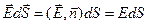 :
:  , но оставшаяся часть интеграла – просто площадь поверхности сферы радиуса r, тогда сразу получаем решение для поля:
, но оставшаяся часть интеграла – просто площадь поверхности сферы радиуса r, тогда сразу получаем решение для поля: 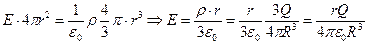 , для поля вне шара(r>=R) все почти то же самое, только справа стоит полный заряд сферы, т.к. тогда он весь помещается в нашу пробную поверхность:
, для поля вне шара(r>=R) все почти то же самое, только справа стоит полный заряд сферы, т.к. тогда он весь помещается в нашу пробную поверхность: 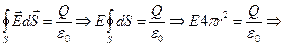
 (вне шара). Потенциал можно найти интегрированием: (предположим что потенциал бесконечности – ноль)
(вне шара). Потенциал можно найти интегрированием: (предположим что потенциал бесконечности – ноль) 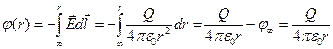 - в случае если потенциал считаем вне шара и
- в случае если потенциал считаем вне шара и  , в итоге мы получили зависимости для потенциала и модуля напряженности поля в шаре и вне его. Кроме того зная эти зависимости мы можем легко найти значение исследуемых величин в специальных точках:
, в итоге мы получили зависимости для потенциала и модуля напряженности поля в шаре и вне его. Кроме того зная эти зависимости мы можем легко найти значение исследуемых величин в специальных точках: 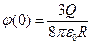 ,
, 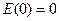 (в центре),
(в центре), 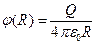
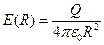 (на поверхности). Построим графики для потенциала и напряженности поля:
(на поверхности). Построим графики для потенциала и напряженности поля:
|
|
|
 (поле для шара)
(поле для шара)
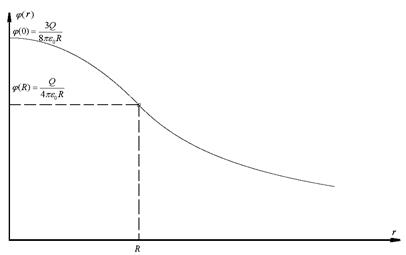 (потенциал для шара)
(потенциал для шара)
Теперь сделаем всё то-же самое для равномерно заряженной сферы:
Теперь если брать замкнутую поверхность внутри сферы, то в ней не окажется зарядов, а значит внутри и не будет электрического поля согласно Теореме Гаусса: 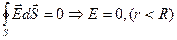 , при переходе через поверхность сферы количесвто заряда внутри нашей замкнутой поверхности увеличивается скачкообразно до Q: и сразу поле становиться ненулевым:
, при переходе через поверхность сферы количесвто заряда внутри нашей замкнутой поверхности увеличивается скачкообразно до Q: и сразу поле становиться ненулевым: 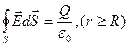 , вычисления подобный для сферы дают следующий результат:
, вычисления подобный для сферы дают следующий результат:  , т.е. отличить сферу от шара находясь вне её невозможно (поля, которые они дают одинаковы). Вычислим теперь потенциал:
, т.е. отличить сферу от шара находясь вне её невозможно (поля, которые они дают одинаковы). Вычислим теперь потенциал: 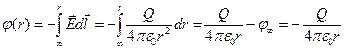 - т.е. вне сферы потенциал в точности совпадает с потенциалом шара с таким же зарядом. А вот внутри сферы дело иначе:
- т.е. вне сферы потенциал в точности совпадает с потенциалом шара с таким же зарядом. А вот внутри сферы дело иначе: 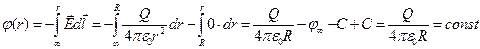 , т.е. изменение потенциала внутри сферы не происходит Значения в особых точках::
, т.е. изменение потенциала внутри сферы не происходит Значения в особых точках:: 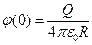 ,
, 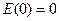 (в центре),
(в центре), 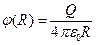
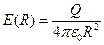
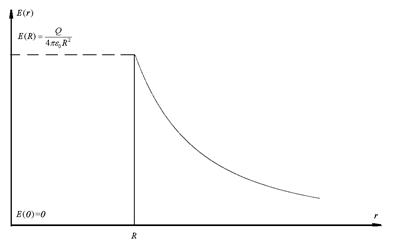 (поле сферы)
(поле сферы)
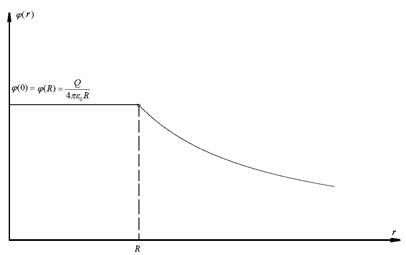 (потенциал сферы)
(потенциал сферы)
2.
Определите поле E вблизи участка металлической поверхности, имеющего поверхностный заряд плотности  . Изобразить линии поля E вблизи этого участка.
. Изобразить линии поля E вблизи этого участка.

|
| E(r)-? |
Решение:
Возьмем цилиндр, как показано на рисунке. (Его образующая перпендикулярна поверхности металла)
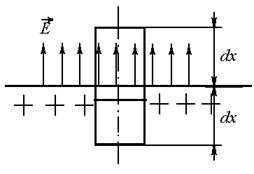 Исходя из симметрии случая бесконечной плоскости, а мы рассматриваем именно его, т.к. в задаче указывается случай близости к поверхности металла, следует что поле на одном и том же расстоянии до плоскости одинаково. Воспользуемся теоремой Гаусса:
Исходя из симметрии случая бесконечной плоскости, а мы рассматриваем именно его, т.к. в задаче указывается случай близости к поверхности металла, следует что поле на одном и том же расстоянии до плоскости одинаково. Воспользуемся теоремой Гаусса:  , здесь Q – заряд, попавший в цилиндр, как известно он весь сосредотачивается на поверхности, а поле внутри металла равно нулю. Тогда мы можем преобразовать интеграл слева:
, здесь Q – заряд, попавший в цилиндр, как известно он весь сосредотачивается на поверхности, а поле внутри металла равно нулю. Тогда мы можем преобразовать интеграл слева:  , при этом вектора мы убрали потому что поле Е направлено перпендикулярно одному из оснований цилиндра. По условию нам так же известна поверхностная плотность заряда на металле, поэтому можем сразу записать:
, при этом вектора мы убрали потому что поле Е направлено перпендикулярно одному из оснований цилиндра. По условию нам так же известна поверхностная плотность заряда на металле, поэтому можем сразу записать: 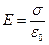 , это и будет поле вблизи заряженной поверхности металла. Замечу, что поле вдали от поверхности может быть любым(все зависит от формы поверхности, наличия других зарядов и т.д.), но около неё оно становиться строго перпендикулярным к поверхности, т.к. геометрически мы переходим к случаю бесконечной заряженной плоскости.
, это и будет поле вблизи заряженной поверхности металла. Замечу, что поле вдали от поверхности может быть любым(все зависит от формы поверхности, наличия других зарядов и т.д.), но около неё оно становиться строго перпендикулярным к поверхности, т.к. геометрически мы переходим к случаю бесконечной заряженной плоскости.
|
|
|
3. Точечный заряд q находиться на расстоянии h от проводящей безграничной плоскости. Определите поверхностную плотность зарядов  , индуцированных на плоскости, и изобразите картину линий поля E между зарядом и плоскостью.
, индуцированных на плоскости, и изобразите картину линий поля E между зарядом и плоскостью. 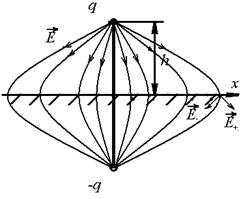
| h,Q |
 (x)-? (x)-?
|
Решение:
На рисунке показано поле, которое создается в данной системе – для его построения мы применили метод зеркальных отображений, заключающийся в том что проводящая бесконечная плоскость ведёт себя в присутствии точечного заряда так будто она – есть отрицательный заряд, расположенный на том же расстоянии что и исходный но с другой стороны. Т.е. благодаря такой конфигурации мы можем определить поле E в любой точке в частности на плоскости как векторную сумму полей зарядов +q и –q, Кроме того известно, что поле перпендикулярно поверхности металла, что и наблюдается в нашем случае: параллельные компоненты вблизи плоскости, складываясь, дают ноль, оставляя только нормальную компоненту. Ранее мы получили связь между полем вблизи плоскости и поверхностной плотностью заряда, индуцированной на проводнике: 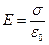 , т.е. нам для решения задачи достаточно найти электрическое поле вблизи плоскости как функцию от x.
, т.е. нам для решения задачи достаточно найти электрическое поле вблизи плоскости как функцию от x. 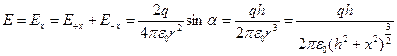 , т.к. поле индуцированное, то заряду нужно добавить знак минус:
, т.к. поле индуцированное, то заряду нужно добавить знак минус: 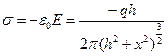
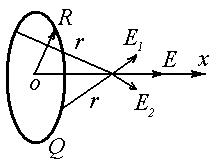
4. Кольцо радиуса R из тонкой проволоки имеет заряд Q(см рис.) Определите зависимости поля E(x) b φ(x) на оси Ox кольца. Построить графики полученных функций. Определить асимптотику полученных зависимостей при x>>R
. 
| R,Q |
| E(x), φ(x)-? |
Решение:
Для решения данной задачи воспользуемся симметрией кольца – если на кольце взять диаметрально противоположные элементы, то поле создаваемое ими в какой бы то не было точке на Ox будет сонаправлено с этой осью. Т.о. Наша задача сводиться к нахождению поля – суммы полей,создаваемых всеми маленькими частями кольца: 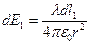
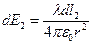 , (здесь
, (здесь 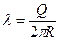 - линейная плотность заряда) а сумма этих двух полей будет состоять только из суммы проекций на Ox, т.к. другие проекции взаимоуничтожаться. Тогда
- линейная плотность заряда) а сумма этих двух полей будет состоять только из суммы проекций на Ox, т.к. другие проекции взаимоуничтожаться. Тогда 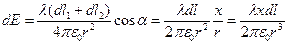 (угол
(угол  - угол между Ox и векторами поля от малых элементов
- угол между Ox и векторами поля от малых элементов 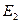 и
и  ), для нахождения полного поля в точке нужно проинтегрировать - только следует помнить, что мы уже учли противоположные элементы – поэтому интегрируем не по всей окружности, но по её половине.
), для нахождения полного поля в точке нужно проинтегрировать - только следует помнить, что мы уже учли противоположные элементы – поэтому интегрируем не по всей окружности, но по её половине. 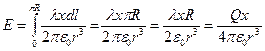 , но из теоремы Пифагора нетрудно заметить:
, но из теоремы Пифагора нетрудно заметить: 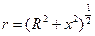 , тогда
, тогда 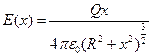 , выражение для потенциала можно найти интегрированием данной функции или просто подсчитать его как сумма потенциалов, создаваемая всеми маленькими частями нашей окружности. Воспользуемся последним:
, выражение для потенциала можно найти интегрированием данной функции или просто подсчитать его как сумма потенциалов, создаваемая всеми маленькими частями нашей окружности. Воспользуемся последним: 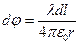 - потенциал, создаваемый каждым маленьким элементом в заданной точке, тогда полный потенциал:
- потенциал, создаваемый каждым маленьким элементом в заданной точке, тогда полный потенциал: 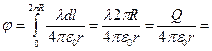
|
|
|
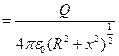 , полученные зависимости для потенциала и поля можно исследовать: возьмём производную
, полученные зависимости для потенциала и поля можно исследовать: возьмём производную 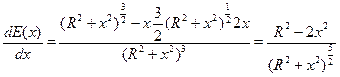 , тогда производная обращается в ноль при
, тогда производная обращается в ноль при 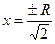 -
- 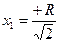 -точка максимума функции.(Т.к. слева от неё производная отрицательна, а справа положительна) В точке максимума значение функции будет:
-точка максимума функции.(Т.к. слева от неё производная отрицательна, а справа положительна) В точке максимума значение функции будет: 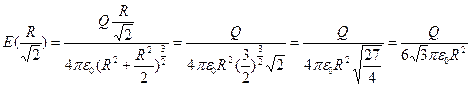
Тогда график полученной зависимости будет иметь следующий вид:
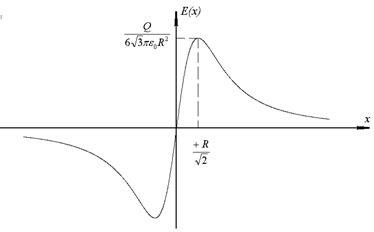 Можно так же показать что:
Можно так же показать что: 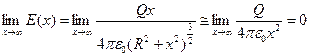 (При больших x R – становиться малым по сравнению с x – издалека наше кольцо становиться похожим на точечный заряд), т.е. при стремлении x к любой из бесконечностей поле стремиться к нулю. Функция поля нечётна, т.е. Слева от кольца мы будем наблюдать всё то же самое, но направление поля будет влево. Теперь займёмся функцией потенциала:
(При больших x R – становиться малым по сравнению с x – издалека наше кольцо становиться похожим на точечный заряд), т.е. при стремлении x к любой из бесконечностей поле стремиться к нулю. Функция поля нечётна, т.е. Слева от кольца мы будем наблюдать всё то же самое, но направление поля будет влево. Теперь займёмся функцией потенциала:  , производная по x:
, производная по x: 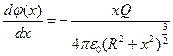 , производная равна нулю только в точке ноль – при этом слева от этой точки она отрицательна, а справа положительна, вследствие чего- это максимум. Значение потенциала в этой точке -
, производная равна нулю только в точке ноль – при этом слева от этой точки она отрицательна, а справа положительна, вследствие чего- это максимум. Значение потенциала в этой точке - 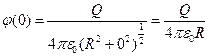
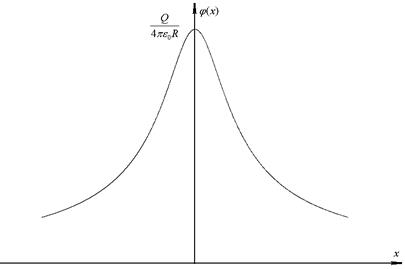
для получения значения на бесконечности найдем предел: 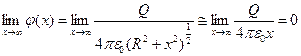 , потенциал также как и поле на бесконечности обращается в ноль.
, потенциал также как и поле на бесконечности обращается в ноль.
5. Вычислить погонные емкости двухпроводной линии и коаксиального кабеля, геометрия которых показана на рисунке.
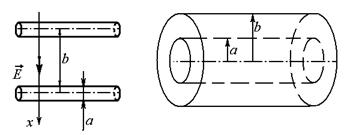
| a,b |
| C-? |
Решение:
Для вычисления емкости воспользуемся определением: 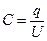 , где q – заряд на каждой из обкладок конденсатора, а U – разность потенциалов между его обкладками.
, где q – заряд на каждой из обкладок конденсатора, а U – разность потенциалов между его обкладками.
1. Двухпроводная линия. Поле заряженной бесконечной цилиндрической поверхности нам известно: 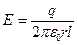 , его можно получить, используя теорему Гаусса окружив наш цилиндр некоторым цилиндром радиуса r, тогда
, его можно получить, используя теорему Гаусса окружив наш цилиндр некоторым цилиндром радиуса r, тогда 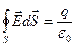
|
|
|
воспользовавшись симметрией поля можно вынести поле за интеграл и тогда просто получить 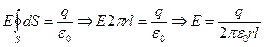 l – длинна охватываемой части проводника, или если ввести линейную плотность заряда, то получим:
l – длинна охватываемой части проводника, или если ввести линейную плотность заряда, то получим: 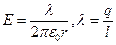 . Теперь рассмотрим нашу задачу – в ней имеются две таких поверхностей (замечу, что в проводящих телах заряд скапливается на поверхности, поэтому их можно считать плоскостями) Для нахождения емкости согласно её определению нам следует найти разность потенциалов между обкладками конденсатора при некотором заряде не обкладках. Разность потенциалов может быть выражена через поле согласно формуле:
. Теперь рассмотрим нашу задачу – в ней имеются две таких поверхностей (замечу, что в проводящих телах заряд скапливается на поверхности, поэтому их можно считать плоскостями) Для нахождения емкости согласно её определению нам следует найти разность потенциалов между обкладками конденсатора при некотором заряде не обкладках. Разность потенциалов может быть выражена через поле согласно формуле: 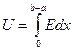 Теперь найдем E(x): Поле в любой точке будет являться суммой полей создаваемой обоими проводами. Суммировать будем не вектора, а их проекции на ось Ox, т.к. поле заряженного цилиндра перпендикулярно его боковой поверхности.
Теперь найдем E(x): Поле в любой точке будет являться суммой полей создаваемой обоими проводами. Суммировать будем не вектора, а их проекции на ось Ox, т.к. поле заряженного цилиндра перпендикулярно его боковой поверхности. 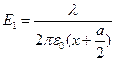
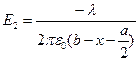 (знак заряда во втором случае меняется - одна обкладка заряжается как положительная другая как отрицательная)
(знак заряда во втором случае меняется - одна обкладка заряжается как положительная другая как отрицательная) 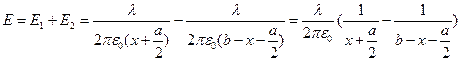 , подставив данное выражение в интеграл:
, подставив данное выражение в интеграл: 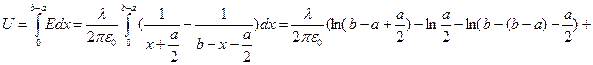
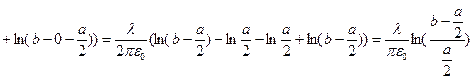 , тогда емкость будет выражаться так:
, тогда емкость будет выражаться так: 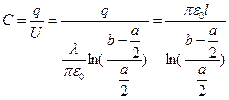 (учтено что
(учтено что  ), тогда емкость линии, приходящаяся на единицу длинны будет:
), тогда емкость линии, приходящаяся на единицу длинны будет:  , кроме того обычно расстояние межу проводами берется много больше их диаметра, вследствие чего можно записать
, кроме того обычно расстояние межу проводами берется много больше их диаметра, вследствие чего можно записать 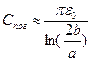
2. Коаксиальный кабель.
Так же применим формулу поля бесконечно длинной заряженной цилиндрической поверхности, при этом внешняя поверхность поля внутри давать не будет, т.к. по теореме Гаусса 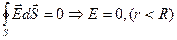 , т.е. поле между обкладками такого конденсатора будет целиком складываться из поля цилиндрической поверхности меньшего радиуса:
, т.е. поле между обкладками такого конденсатора будет целиком складываться из поля цилиндрической поверхности меньшего радиуса: 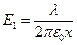 , тогда разность потенциалов между обкладками будет рассчитываться по формуле:
, тогда разность потенциалов между обкладками будет рассчитываться по формуле: 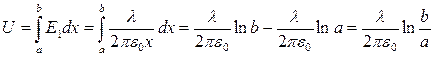 , а емкость
, а емкость 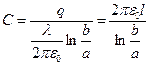 , погонная емкость:
, погонная емкость: 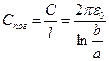
6. Определите максимальный заряд, который способна нести металлический шар радиуса R=10см в воздухе и соответствующий потенциал этого шара, если электрическая прочность воздуха  (напряженность при которой наступает электрический пробой).
(напряженность при которой наступает электрический пробой).
R=10см
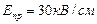
|
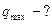
|
Решение:
Функция поля шара(вне его т.е. при r>R) в зависимости от расстояния до его центра – величина известная: 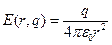 - поле максимально вблизи поверхности шара(если пробьет то около поверхности), т.е. пробой наступает при
- поле максимально вблизи поверхности шара(если пробьет то около поверхности), т.е. пробой наступает при 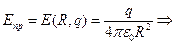
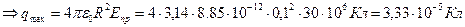 При данном заряде сфера будет уже не способна удерживать его – с поверхности сферы заряд начнёт утекать в воздух, ионизируя его.
При данном заряде сфера будет уже не способна удерживать его – с поверхности сферы заряд начнёт утекать в воздух, ионизируя его.
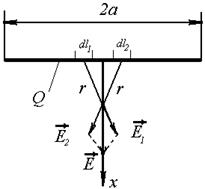
7. Находящийся в вакууме тонкий прямой стержень длинны 2a заряжен равномерно зарядом Q. Найти напряженность поле E как функцию расстояния x от центра стержня до точки прямой, перпендикулярной к стержню и проходящей через его центр. Исследовать полученную зависимость при x>>a
|
|
|
| a,Q |
| E(x)-? |
Решение:
Для решения разобьем наш стержень на маленькие элементы dl, они имеют некоторый заряд, который мы будем определять, задав линейную плотность заряда: 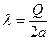 , а
, а 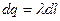 , заряды таких маленьких элементов можно считать точечными и поэтому поле в некоторой точке на Ox будет складываться из поля всех таких элементов. Однако поиск этой суммы можно упростить – рассмотрев два симметричных элемента и поля, которые они создают:
, заряды таких маленьких элементов можно считать точечными и поэтому поле в некоторой точке на Ox будет складываться из поля всех таких элементов. Однако поиск этой суммы можно упростить – рассмотрев два симметричных элемента и поля, которые они создают: 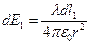
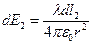 , при этом при проецировании на оси эти поля дадут результирующие поле совпадающие с Ox. Т.е. теперь говоря о поле, которое создает стержень, мы будем говорить именно о его составляющей на Ox, т.к. только она имеет ненулевую величину.
, при этом при проецировании на оси эти поля дадут результирующие поле совпадающие с Ox. Т.е. теперь говоря о поле, которое создает стержень, мы будем говорить именно о его составляющей на Ox, т.к. только она имеет ненулевую величину. 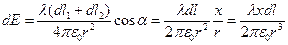 (угол
(угол  - угол между Ox и векторами поля от малых элементов
- угол между Ox и векторами поля от малых элементов 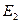 и
и  ) интегрирование ведётся по l:
) интегрирование ведётся по l: 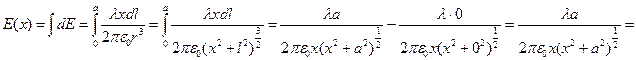
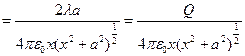 (здесь был применён табличный интеграл:
(здесь был применён табличный интеграл:  ) Перепишем полученную формулу и выполним исследование зависимости:
) Перепишем полученную формулу и выполним исследование зависимости: 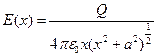 ,
, 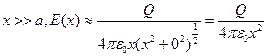 - т.е. при удалении на большое расстояние от этого стержня его поле будет все более и более походить на поле точечного заряда – и действительно с большого расстояния геометрия тела перестает сильно влиять на поле: мы видим стержень как точку.
- т.е. при удалении на большое расстояние от этого стержня его поле будет все более и более походить на поле точечного заряда – и действительно с большого расстояния геометрия тела перестает сильно влиять на поле: мы видим стержень как точку.
8. Тонкое проволочное кольцо имеет радиус R и заряд Q. Кольцо расположено параллельно бесконечной проводящей плоскости. На расстоянии h от неё. Найти поверхностную плотность заряда в точке плоскости, расположенной симметрично относительно кольца.
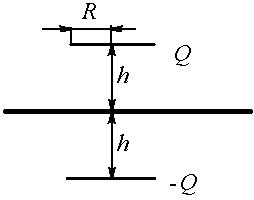
| R,Q,h |
 -? -?
|
Решение:
Для решения данной задачи применим формулу для поля у поверхности проводника: 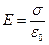 (см. так же зад №3), далее нам просто надо найти поле в точке симметрии – кстати, это точка – основание перпендикуляра, опущенного на плоскость из центра кольца. Применим метод зеркальных отображений: индуцированные заряды будут создавать поле так, будто за проводящей плоскостью – такое же кольцо, но заряженное противоположно. Поле в точке симметрии такой системы будет складываться из того и другого поля:
(см. так же зад №3), далее нам просто надо найти поле в точке симметрии – кстати, это точка – основание перпендикуляра, опущенного на плоскость из центра кольца. Применим метод зеркальных отображений: индуцированные заряды будут создавать поле так, будто за проводящей плоскостью – такое же кольцо, но заряженное противоположно. Поле в точке симметрии такой системы будет складываться из того и другого поля: 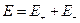 , при этом мы знаем как ведёт себя поле по оси кольца (см. зад №4) Из неё нам потребуется лишь зависимость
, при этом мы знаем как ведёт себя поле по оси кольца (см. зад №4) Из неё нам потребуется лишь зависимость  . У нас x=h, тогда получим выражение для поля около плоскости:
. У нас x=h, тогда получим выражение для поля около плоскости:  , тогда можем применить формулу для поверхностной плотности:
, тогда можем применить формулу для поверхностной плотности: 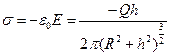 , минус добавляем, т.к. заряд индуцированный и имеет противоположный знак.
, минус добавляем, т.к. заряд индуцированный и имеет противоположный знак.
9. Конденсатор 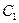 зарядили до напряжения
зарядили до напряжения 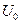 и отключили от источника. Затем параллельно к нему подключили конденсатор емкости
и отключили от источника. Затем параллельно к нему подключили конденсатор емкости 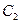 . Определить энергию, израсходованную на образование искры при соединении конденсаторов.
. Определить энергию, израсходованную на образование искры при соединении конденсаторов.
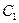 , , 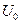 , , 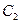
|
| W-? |
Решение:
После первоначальной зарядки конденсатор накопил в себе энергию 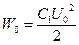 . После соединения и перехода системы к установившемся режиму напряжения на конденсаторах обязаны сравняться. И кроме того никуда не мог деться заряд – закон сохранения заряда. Применим эти суждения для поиска этого установившегося напряжения конденсаторов.
. После соединения и перехода системы к установившемся режиму напряжения на конденсаторах обязаны сравняться. И кроме того никуда не мог деться заряд – закон сохранения заряда. Применим эти суждения для поиска этого установившегося напряжения конденсаторов.
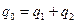
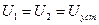 , воспользовавшись определением емкости, преобразуем эти формулы:
, воспользовавшись определением емкости, преобразуем эти формулы:  , тогда запишем закон сохранения энергии в таком виде:
, тогда запишем закон сохранения энергии в таком виде: 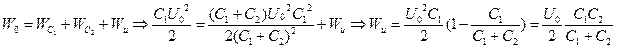 , так мы получили энергию, уходящую из системы, расходуемую на искру.
, так мы получили энергию, уходящую из системы, расходуемую на искру.
Раздел 2. Магнитостатика.Электромагнитная индукция.
1. По круговому витку радиуса R из тонкого провода течет ток i. Определить магнитное поле B на оси витка и построить соответствующий график. Изобразите примерную картину линий поля B в осевом сечении рисунка.
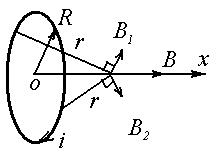
| i,R |
| B(x) |
Решение:
Для решения данной задачи будем использовать закон Био-Савара-Лапласа:
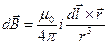 , т.е. это магнитное поле, которое создается некоторым маленьким элементом dl с током i, магнитные поля обладают свойством суперпозиции, как и электрические, поэтому магнитное поле в данной точке есть сумма всех полей, создаваемых различными токами.
, т.е. это магнитное поле, которое создается некоторым маленьким элементом dl с током i, магнитные поля обладают свойством суперпозиции, как и электрические, поэтому магнитное поле в данной точке есть сумма всех полей, создаваемых различными токами.
Для начала возьмем два диаметрально противоположных малых элементов тока 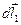
 , тогда поля создаваемые ими в некоторой точке на оси кольца будут иметь вид:
, тогда поля создаваемые ими в некоторой точке на оси кольца будут иметь вид: 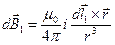
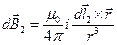 , тогда проекция на оси перпендикулярные к Ox дают ноль, а проекция на Ox будет
, тогда проекция на оси перпендикулярные к Ox дают ноль, а проекция на Ox будет 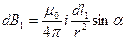 и аналогично для
и аналогично для  , но в сумме они дадут:
, но в сумме они дадут:  (здесь и далее рассматриваем проекцию на ось Ox равную так же модулю поля- его величине), а кроме того
(здесь и далее рассматриваем проекцию на ось Ox равную так же модулю поля- его величине), а кроме того 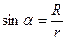 , тогда получается такая зависимость малого вклада двух противоположных элементов от расстояния их до точки на Ox:
, тогда получается такая зависимость малого вклада двух противоположных элементов от расстояния их до точки на Ox:  (из прямоугольного треугольника) Интегрирование будем проводить по половине дуги окружности, т.к. другую половину мы уже учли:
(из прямоугольного треугольника) Интегрирование будем проводить по половине дуги окружности, т.к. другую половину мы уже учли: 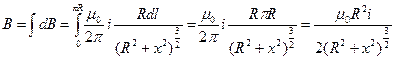 В данном случае мы определили модуль поля. Его направление следует определять по правилу правого винта в векторном произведении при различных случаях направления течения тока. Определим картину линий магнитного поля на данном рисунке:
В данном случае мы определили модуль поля. Его направление следует определять по правилу правого винта в векторном произведении при различных случаях направления течения тока. Определим картину линий магнитного поля на данном рисунке:
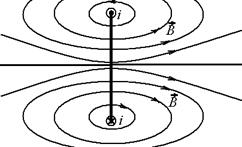
Способ построения линий заключался в том, чтобы примерно представить, что вокруг каждого малого элемента с током крутиться множество векторов  .Чем дальше от этого элемента, тем более другие элементы воздействуют на это поле.
.Чем дальше от этого элемента, тем более другие элементы воздействуют на это поле.
2. Постоянный ток I течёт в прямом и обратном направлении по коаксиальному кабелю. Найти магнитное поле во всем пространстве. Построить график 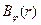 при
при 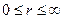 . Изобразить поле B в осевом сечении линии.
. Изобразить поле B в осевом сечении линии. 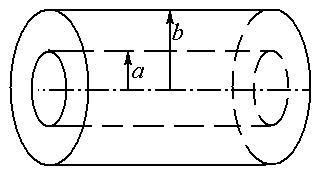
| a,b,I |
| B(r)-? |
Решение:
Для решения данной задачи Воспользуемся теоремой о циркуляции магнитного поля при постоянных токах (токов смещения нет)
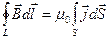 , здесь L –некоторый замкнутый контур, а S – натянутая на него поверхность. Будем выбирать L –коаксиальные с кабелем кольца (т.е. оси колец и кабеля - все совпадают) Натягивать будем на них просто круг. Очевидно, что при
, здесь L –некоторый замкнутый контур, а S – натянутая на него поверхность. Будем выбирать L –коаксиальные с кабелем кольца (т.е. оси колец и кабеля - все совпадают) Натягивать будем на них просто круг. Очевидно, что при  Циркуляция магнитного поля будет равна нулю, т.к. токи в наш контур не попадают. При
Циркуляция магнитного поля будет равна нулю, т.к. токи в наш контур не попадают. При 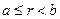 в наш контур попадают токи от внутренней цилиндрической поверхности. Тогда можно записать,
в наш контур попадают токи от внутренней цилиндрической поверхности. Тогда можно записать, 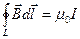 , здесь I – полный ток проходящий через S. Из соображений симметрии поле на одинаковом расстоянии от оси одинаково, и кроме того направлено по касательной к L, тогда в итоге мы можем записать:
, здесь I – полный ток проходящий через S. Из соображений симметрии поле на одинаковом расстоянии от оси одинаково, и кроме того направлено по касательной к L, тогда в итоге мы можем записать: 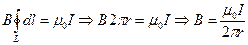 . В случае же
. В случае же  в левой части снова становится ноль – т.к. по внешней части кабеля ток течет в противоположную сторону.
в левой части снова становится ноль – т.к. по внешней части кабеля ток течет в противоположную сторону. 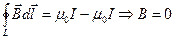 , т.е. поле вне коаксиального кабеля отсутствует.
, т.е. поле вне коаксиального кабеля отсутствует.
График такой:
 Для изображения поля вспомним, что в принципе случай между двумя цилиндрическими поверхностями похож на поле прямого провода с током, а вне кабеля поля нет как и внутри обоих оплеток:
Для изображения поля вспомним, что в принципе случай между двумя цилиндрическими поверхностями похож на поле прямого провода с током, а вне кабеля поля нет как и внутри обоих оплеток: 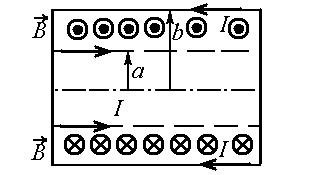 поле определяем по правилу правого винта (буравчика).
поле определяем по правилу правого винта (буравчика).
3. Постоянный ток I равномерно распределен по сечению длинного провода радиуса R. Определить магнитное поле внутри и вне провода. Построить график 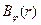 при
при 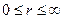 .
.
| R,I |
| B(r)-? |
Решение:
Для решения так же воспользуемся законом о циркуляции магнитного поля при постоянных токах: 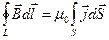 , заметим симметрию – поле на одном и том же расстоянии от оси будет одинаково. Тогда мы можем написать следующее:
, заметим симметрию – поле на одном и том же расстоянии от оси будет одинаково. Тогда мы можем написать следующее: 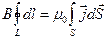 , под L мы будем понимать круговой коаксиальный с проводом контур, а S – круг, натянутый на L. Тогда произведение плотности тока на площадку через которое он протекает, может быть записано как просто произведение скалярных величин:
, под L мы будем понимать круговой коаксиальный с проводом контур, а S – круг, натянутый на L. Тогда произведение плотности тока на площадку через которое он протекает, может быть записано как просто произведение скалярных величин: 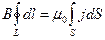 , кроме того по условию задачи ток распределен по проводу равномерно, поэтому плотность тока можно вынести за знак интеграла:
, кроме того по условию задачи ток распределен по проводу равномерно, поэтому плотность тока можно вынести за знак интеграла: 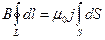 , а под интегралами остались простые величины – длинна контура и его площадь(в случае если радиус контура превышает радиус провода, то его площадь равна площади поперечного сечения провода):
, а под интегралами остались простые величины – длинна контура и его площадь(в случае если радиус контура превышает радиус провода, то его площадь равна площади поперечного сечения провода):  , если вспомнить как выражается плотность тока(
, если вспомнить как выражается плотность тока(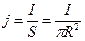 ), то
), то  , теперь можем построить график:
, теперь можем построить график:
Максимальное значение магнитного поля – на поверхности 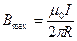
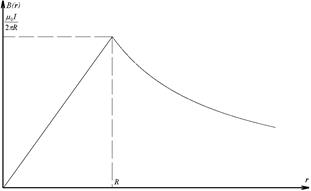
4. Электрон, ускоренный разницей потенциалов U=1кВ, влетает в однородное постоянное магнитное поле B=1Тл под углом 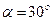 к вектору B. Изобразите траекторию электрона в магнитном поле и определите шаг и радиус спирали.
к вектору B. Изобразите траекторию электрона в магнитном поле и определите шаг и радиус спирали.
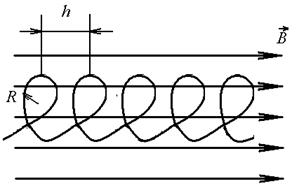
U=1кВ
B=1Тл
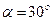
|
| R-?;h-? |
Решение:
Магнитное поле будет, благодаря магнитной составляющей силе Лоренца, действовать на электрон. При этом сила этого действии будет направлена всегда перпендикулярно к скорости электрона. Разложим скорость электрона на две составляющие: по магнитному полю и перпендикулярно ему.  , тогда по формуле для магнитной составляющей силы Лоренца будем иметь:
, тогда по формуле для магнитной составляющей силы Лоренца будем иметь: 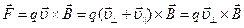 (векторное произведение двух сонаправленных векторов=0) т.о. мы определили силу. Эта сила – центростремительная – в системе отсчета, где электрон покоится или движется равномерно или прямолинейно на него так же действует центробежная сила, а условие равновесия электрона можно записать как:
(векторное произведение двух сонаправленных векторов=0) т.о. мы определили силу. Эта сила – центростремительная – в системе отсчета, где электрон покоится или движется равномерно или прямолинейно на него так же действует центробежная сила, а условие равновесия электрона можно записать как:  (здесь и далее
(здесь и далее 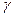 - удельный заряд электрона – отношение заряда электрона к его массе
- удельный заряд электрона – отношение заряда электрона к его массе  ) Для определения скорости электрона воспользуемся законом сохранения энергии: энергия электрического поля разгона перешла в кинетическую энергию движения электрона:
) Для определения скорости электрона воспользуемся законом сохранения энергии: энергия электрического поля разгона перешла в кинетическую энергию движения электрона:  ,тогда окончательную формулу для вычисления радиуса спирали:
,тогда окончательную формулу для вычисления радиуса спирали: 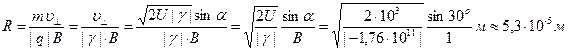
Шагом спирали называется длинна поступательного перемещения электрона за время одного периода его вращательного движения. Период вращательного движения определятся исходя из времени прохождения его по окружности радиуса R: 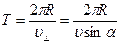 , тогда расстояние, которое прошел электрон поступательно будет:
, тогда расстояние, которое прошел электрон поступательно будет: 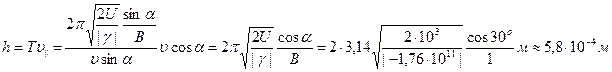
5. Металлический диск радиуса R=10см вращается вокруг своей оси с постоянной угловой скоростью, совершая 100 об/сек, в перпендикулярном к диску однородном магнитном поле индукции B=0,1 Тл. Определить ЭДС индукции между осью и ободом диска.
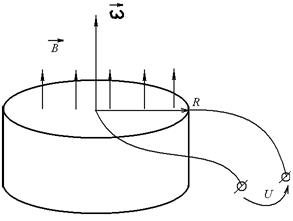
| R=10см v=100 1/с B=0,1Тл |
| Е-? |
Решение:
В диске, благодаря вращению и наличию магнитного поля, создается центробежная сила, которая по всему радиусу двигает заряженные частицы от центра к периферии(или наоборот – зависит от знака основных носителей тока), Рассмотрим некоторый заряд внутри этого цилиндра, т.к. по условию он- металлический, то носителями электрического тока будут электроны. Рассмотрим теперь уравнение динамики электрона в системе отсчета связанной с вращающимся диском. В такой системе на электрон будет действовать направленная к центру или от него, тогда: 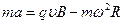 (в проекции на радиус) слагаемым обычной центробежной силы можно пренебречь т.к. численно они несравнимы:
(в проекции на радиус) слагаемым обычной центробежной силы можно пренебречь т.к. численно они несравнимы: 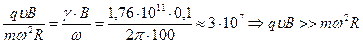 , тогда получим простое уравнение динамики.
, тогда получим простое уравнение динамики. 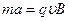 , сила действующая со стороны магнитного поля
, сила действующая со стороны магнитного поля  зависит от расстояния данной заряженной частицы до оси вращения: работа будет выглядеть как интеграл:
зависит от расстояния данной заряженной частицы до оси вращения: работа будет выглядеть как интеграл: 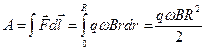 , тогда согласно определению ЭДС это отношение работы требуемой для перемещения заряда, к величине заряда.
, тогда согласно определению ЭДС это отношение работы требуемой для перемещения заряда, к величине заряда. 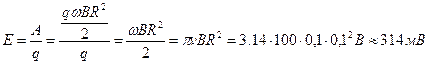
6. Определите погонную индуктивность двухпроводной линии, если a=0,5 см, b=10см. Магнитная проницаемость всюду равна 1, а полем внутри проводов можно пренебречь.
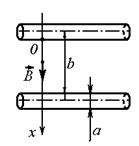
| a=0,5 см b=10 см |
| L-? |
Решение:
В данном случае индуктивность будет выражаться как самоиндукция: 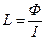 Найдем поток через контур между проводами: Нам известна формула для величины поля на некотором расстоянии от цилиндрического провода:
Найдем поток через контур между проводами: Нам известна формула для величины поля на некотором расстоянии от цилиндрического провода: 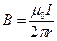 , исходя из этой формулы, а так же из того, что магнитное поле обладает свойством суперпозиции можно записать величину поля в зависимости от координаты x:
, исходя из этой формулы, а так же из того, что магнитное поле обладает свойством суперпозиции можно записать величину поля в зависимости от координаты x: 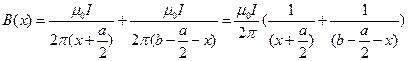 , можем найти поток – поверхность, по которой будем считать: выберем исходя из пренебрежения задачи, что полем внутри проводов можно пренебречь, а уж тем более полем за проводами, где оно есть разность магнитных полей создаваемых проводами.
, можем найти поток – поверхность, по которой будем считать: выберем исходя из пренебрежения задачи, что полем внутри проводов можно пренебречь, а уж тем более полем за проводами, где оно есть разность магнитных полей создаваемых проводами. 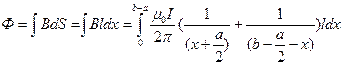 , преобразование
, преобразование 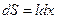 возможно благодаря тому что поле по длине проводов не меняется. Тогда после интегрирования получим:
возможно благодаря тому что поле по длине проводов не меняется. Тогда после интегрирования получим: 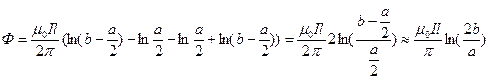 , тогда
, тогда 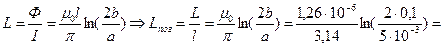
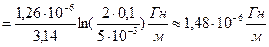
7. Определите погонную индуктивность коаксиальной линии, если  , магнитная проницаемость
, магнитная проницаемость 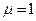 , а полем внутри проводов можно пренебречь.
, а полем внутри проводов можно пренебречь.
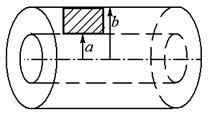

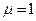
|
| L-? |
Решение:
Магнитное поле коаксиального кабеля полностью сосредоточено между двумя его оплетками, т.е. без нарушения точности подсчета мы будем рассматривать поток как показано на рисунке (Радиус принадлежит этой площадке). Мы знаем, что цилиндрическая поверхность не создает внутри себя никакого магнитного поля, а значит, от внешней оплетки никакого влияния не будет, тогда зависимость поля от расстояния до оси будет иметь вид:  , сразу находим поток:
, сразу находим поток:  , тогда индуктивность выразится так:
, тогда индуктивность выразится так: 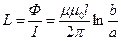 , а погонная индуктивность:
, а погонная индуктивность: 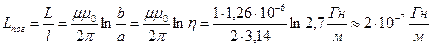
18. Вычислить взаимную индуктивность M длинного прямого провода и прямоугольной рамки, лежащей с ним в одной плоскости. Определите асимптотику зависимости M(r) r>>a.
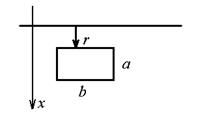
| a,b,r |
| M(r)-? |
Решение:
Взаимная индуктивность определяется формулой  , однако Ф – поток в одном контуре, а I – ток в другом. При этом взаимная индуктивность в отсутствии ферромагнетиков не зависит от тока, т.е. мы можем выбрать произвольный ток в одном из контуров, а затем подсчитать поток, который тот создает в другом контуре, что мы и сделаем. Пусть в проводе течет ток I. Тогда на расстоянии x от него есть магнитное поле равное по величине
, однако Ф – поток в одном контуре, а I – ток в другом. При этом взаимная индуктивность в отсутствии ферромагнетиков не зависит от тока, т.е. мы можем выбрать произвольный ток в одном из контуров, а затем подсчитать поток, который тот создает в другом контуре, что мы и сделаем. Пусть в проводе течет ток I. Тогда на расстоянии x от него есть магнитное поле равное по величине  . Оно радиально симметрично, т.е. зависит только от расстояния, но тогда поток в контуре может быть выражен:
. Оно радиально симметрично, т.е. зависит только от расстояния, но тогда поток в контуре может быть выражен: 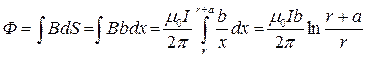 , тогда
, тогда 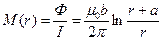 , при r>>a получаем:
, при r>>a получаем: 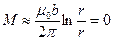
9. Прямоугольная рамка и длинный прямой провод с током I находятся в одной плоскости. Рамку поступательно перемещают в плоскости рисунка с постоянной скоростью v, удаляя ее от провода, найти ЭДС индукции в рамке, как функцию расстояния ее от провода.
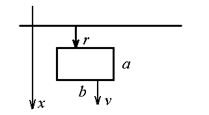
| a,b,r |
| E(r)-? |
Решение:
Для нахождения ЭДС индукции воспользуемся законом Фарадея:  поле, создаваемое на расстоянии x, от провода может быть найдено по формуле:
поле, создаваемое на расстоянии x, от провода может быть найдено по формуле:  и поток тогда мы можем найти как
и поток тогда мы можем найти как  , теперь подставим его в формулу для ЭДС:
, теперь подставим его в формулу для ЭДС: 
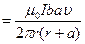 (здесь учтено что скорость есть первая производная по времени от расстояния
(здесь учтено что скорость есть первая производная по времени от расстояния 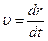 ). Нашли таким образом:
). Нашли таким образом: 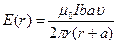
10. В длинном прямом соленоиде с радиусом обмотки a и числом витков на единицу длины n изменяют ток с постоянной скоростью 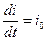 Найти модуль напряженности вихревого электрического поля E как функцию расстояния r до оси соленоида. Построить график полученной зависимости и нарисовать примерную картину поля E.
Найти модуль напряженности вихревого электрического поля E как функцию расстояния r до оси соленоида. Построить график полученной зависимости и нарисовать примерную картину поля E.
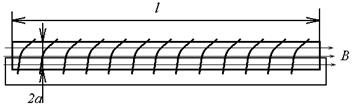
a, 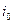 ,n ,n
|
| E(r)-? |
Решение:
Для решения данной задачи воспользуемся одним из уравнений Максвелла:
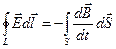 , т.к. в нашей задаче характеристики поверхности S по времени меняться не будут, то производную по времени можно вынести за знак интеграла:
, т.к. в нашей задаче характеристики поверхности S по времени меняться не будут, то производную по времени можно вынести за знак интеграла:  . Из свойств симметрии соленоида следует, что поле E – будет одинаково на одном и том же расстоянии от оси соленоида, тогда вынесем E знак интеграла, кроме того избавимся от векторов в левой части, выбрав в качестве l – окружность, коаксиальную соленоиду. Тогда:
. Из свойств симметрии соленоида следует, что поле E – будет одинаково на одном и том же расстоянии от оси соленоида, тогда вынесем E знак интеграла, кроме того избавимся от векторов в левой части, выбрав в качестве l – окружность, коаксиальную соленоиду. Тогда: 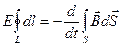
Теперь наша задача состоит в том, чтобы подсчитать поток магнитного поля через S – круг, натянутый на L. Мы рассматриваем модель длинного соленоида, т.е. его длинна много больше радиуса сечения. Тогда решим следующую задачу: найти поле создава
|
|
|


