 |
Интегральная теорема Муавра - Лапласа (без доказательства).
|
|
|
|
Интегральная теорема Лапласа. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р(0<p<1), событие наступит не меньше k1 раз и не более k2 раз, приближенно равна: P(k1;k2)=Ф(х’’) – Ф(х’). Здесь Ф(х)=1/(корень из 2пи) * интеграл от0 до х е в степени –(z*2/2)dz – функция Лапласа, х’=(k1 – np)/(корень из npq), х’’=(k2 – np)/(корень из npq).
30. Интегральная теорема Муавра-Лапласа (без доказательств)


31. Системы двух с.в.; совместный закон распределения д.с.в.; закон распределения составляющих
Законом распределения дискретной двумерной случ величины называют перечень возможных значений этой величины, т.е. пар чисел (xi, yj) и их вероятностей P(xi, yj).
| y/x | x1 | x2 | … | xn |
| y1 | p(x1, y1) | p(x2, y1) | … | p(xn, y1) |
| y2 | p(x1, y2) | p(x2, y2) | … | p(xn, y2) |
| … | … | … | … | … |
| ym | p(x1, ym) | p(x2, ym) | … | p(xn, ym) |
Зная закон распределения двумерной дискретной случ величины, можно найти законы распределения каждой из составляющих. Например: События (X=x1, Y=y1)…(X=x1, Y=Ym) – несовместны, поэтому вероятность P(x1) того, что Х примет значение х1, по теореме сложения такова: P(x1)=p(x1, y1)+…+p(x1, ym). Т.о. вероятность того, что Х примет значение xi, равна сумме вероятностей «столбца хi». Аналогично, сложив «строки Yj», получим вероятность P(Y=yj).
32. Функция распределения двумерной случайной величины
Систему случ чисел величин X и Y изображают случ точкой на плоскости с координатами (X,Y), тогда вместо т. используется понятие случ вектора. Функция распределения системы 2х случ величин называется вероятностью совместного выполнения двух неравенств:
P(x,y)=P(X<x)P(Y<y). Геометрически это означает, что функция распределения есть вероятность попадания случ точки в бесконечный квадрат с вершиной в точке (X,Y), лежащий ниже и левее этой точки.
|
|
|
Свойства функции распределения:
1. x2>x1, F(x2,y)≥F(x1,y)
y2>y1, F(x,y2)≥F(x, y1)
2. F(x,-∞)=F(-∞,y)=F(-∞,-∞)=0
3. F(∞,∞)=1
4. F(x, ∞)=F(x); F(∞,y)=F(y);
33. Вероятность попадания случайной точки в прямоугольник
С помощью  , можно вычислять вероятности попадания случайной точки в прямоугольник:
, можно вычислять вероятности попадания случайной точки в прямоугольник:



34. Плотность вероятностей непрерывной д.в.с.; вероятность попадания случайной точки в произвольную область.
Плотностью распределения системы 2х случ величин называется вторая смешанная частная производная от функции распределения:
P((x,y)cP∆)=F(x+∆x, y+∆y)-F(x+∆x, y)-F(x, y+∆y)+F(x,y)

Плотность распределения системы случ величин представляет собой плотность распределения массы в точке с координатами x,y.
f(x,y)dxdy
Элем. вероятность f(x,y)dxdy есть вероятность попадания в элемент. прямоугольник со сторонами dx, dy. Эта вероятность равна объему параллелепипеда, ограниченного сверху поверхностью f(x,y) и отражающегося на элементарный участок dxdy.

Свойства плотности:
1. f(x,y)≥0
 - полный объем тела, ограниченного поверхностью распределения с плоскостью xOy = 1.
- полный объем тела, ограниченного поверхностью распределения с плоскостью xOy = 1.
35. Условные законы распределения составляющих системы двух случайных величин
Рассмотрим дискретную двумерную случайную величину и найдем закон распределения составляющей Х при условии, что Y примет определенное значение (например, Y = у 1). Для этого воспользуемся формулой Байеса, считая гипотезами события Х = х 1, Х = х 2,…, Х = хп, а событием А – событие Y = у 1. При такой постановке задачи нам требуется найти условные вероятности гипотез при условии, что А произошло. Следовательно,
 .
.
Таким же образом можно найти вероятности возможных значений Х при условии, что Y принимает любое другое свое возможное значение:

Аналогично находят условные законы распределения составляющей Y:
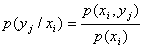
36. Математическое ожидание и дисперсия системы двух случайных величин. Условное мат. Ожидание
|
|
|


Условным математическим ожиданием дискретной случайной величины Y при X = x (х – определенное возможное значение Х) называется произведение всех возможных значений Y на их условные вероятности.

Для непрерывных случайных величин:
 ,
,
где f(y/x) – условная плотность случайной величины Y при X=x.
37. Зависимые и независимые случайные величины. Теоремы о необходимых и достаточных условиях независимости
2 случ величины называются независимыми, если закон распределения одной из них не зависит от того, какие возможные значения приняла другая величина. Следовательно, условные распределения независимых величин равны их безусловным распределениям.
Теорема: Для того, чтобы случайные величины X и Y были независимыми, необходимо и достаточно, чтобы функция распределения системы (X, Y) была равна произведению функций распределения составляющих:
F(x, y)=F1(x)F2(y)
Следствие: Для того, чтобы непрерывные случайные величины X и Y были независимыми, необходимо и достаточно, чтобы плотность совместного распределения системы (X, Y) была равна произведению плотностей распределения составляющих:
f(x, y)=f1(x)f2(y)
38. Системы двух случайных величин. Корреляционный момент. Коэффициент корреляции


39. Линейная регрессия. Прямые линии среднеквадратической регрессии

Пример: 
40. Числовые характеристики коррелированных случайных величин.
Случайные величины называются коррелированными, если их корреляционный момент отличен от нуля, и некоррелированными, если их корреляционный момент равен нулю.
Корреляционным моментом mxy случайных величин Х и Y называется математическое ожидание произведения отклонений этих величин.

Корреляционный момент служит для того, чтобы охарактеризовать связь между случайными величинами. Если случайные величины независимы, то их корреляционный момент равен нулю.
Коэффициентом корреляции rxy случайных величин Х и Y называется отношение корреляционного момента к произведению средних квадратических отклонений этих величин.
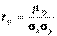
Коэффициент корреляции является безразмерной величиной. Коэффициент корреляции независимых случайных величин равен нулю.
41. Функции одной случайной величины; числовые характеристики; закон распределения
|
|
|
Если каждому возможному значению случайной величины Х соответствует одно возможное значение случайной величины Y, то Y называют функцией случайного аргумента X: Y=φ(X).

При записи закона распределения вероятности y руководствуются следующими правилами:
1. Если различным возможным значениям X соответствуют различные возможные значения Y, то вероятности соответствующих значений X и Y равны между собой: P(X=xi)=P(y=f(xi))=pi.
2.Если различным возможным значениям Х соответствуют значения Y, среди которых есть равные между собой, то следует складывать вероятности повторяющихся значений Y.
42. Функции двух случайных величин
Если каждой паре возможных значений случ величин X и Y соответствует одно возможное значение случайной величины Z, то Z называют функцией двух случ аргументов X и Y: Z=φ(X, Y).
1. Пусть X и Y – дискретные независимые случ величины. Для того, чтобы составить закон распределения функции Z=X+Y, надо найти все возможные значения Z и их вероятности. Т.к. X и Y независимые случ величины, то zi=xi+yi, pz=px*py. Если zi=zj, то их вероятности складываются.
2. Пусть X и Y – непрерывные случ величины. Доказано: если X и Y независимы, то плотность распределения g(z) суммы Z=X+Y (при условии, что плотность хотя бы одного из аргументов задана на интервале(-∞;∞) одной формулой) может быть найдена с помощью формулы:
 , где f1, f2 – плотности распределения аргументов.
, где f1, f2 – плотности распределения аргументов.
Если возможные значения аргументов неотрицательны, то g(z) находят по формуле: 
Плотность распределения суммы независимых случ величин называют композицией, а закон распределения вероятностей называют устойчивым, если композиция таких законов есть тот же закон. M(z)=M(x)+M(y); D(z)=D(x)+D(y).
43. Закон распределения суммы двух случайных величин. Композиция законов распределения
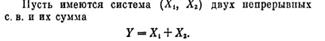

44. Случайные функции; определение; способы задания 

45. Математическое ожидание случайной функции; ее свойства


46. Дисперсия случайной функции; ее свойства



47. Корреляционная функция случайной функции; ее свойства




|
|
|


48. Взаимная корреляционная функция двух случайных функций; ее свойства




49. Сумма случайных функций и ее характеристики




50. Каноническое разложение случайных функций
Существует несколько способов
аналитического представления случайных процессов. Удобно использовать так
называемую элементарную случайную функцию, которая представляется в
виде:
x (t) = V ×j(t)
Рассмотрим случайную функцию (процесс) x (t), представленную в виде
суммы её математического ожидания mx и элементарных случайных функций:

Каноническое разложение корреляционной функции и каноническое разложение дисперсии:

51. Стационарные случайные функции; определение; основные свойства

52. Корреляционная функция стационарной случайной функции; ее свойства


53. Свойство эргодичности случайной функции. Достаточные условия эргодичности



54. Представление стационарной случайной функции в виде гармонических колебаний со случайными амплитудами и фазами


|
|
|


