 |
Дифференциальные уравнения
|
|
|
|
Интегралы, Дифференциальные уравнения, Ряды
(для заочного факультета)
В соответствии с программой курса высшей математики во 2 семестре настоящее пособие включает три разделы:
1) интегральное исчисление,
2) дифференциальные уравнения,
3) ряды.
Приводится необходимый теоретический материал и разбор типовых задач из указанных разделов с подробными решениями.
Кроме того, в приложении 1 представлен тренировочный тест с ответами для самоконтроля знаний.
Материал данной работы рекомендуется использовать для подготовки к контрольной работе и экзамену по высшей математике на заочном факультете.
Самара
Самарский государственный технический университет
Интегралы
Определение и ОСНОВНЫе свойства
Неопределенного интеграла
1. Постоянный множитель можно выносить за знак неопределённого интеграла
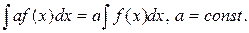
2. Неопределённый интеграл от суммы функций равен сумме интегралов от этих функций, если интегралы существуют

ТАБЛИЦА интегралов
ОСНОВНЫХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
1. 
2. 

Частный случай 

3. 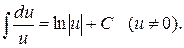
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 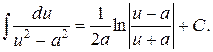
15. 
16. 
17. 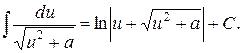
18. Формула интегрирования по частям
 .
.
19. Формула Ньютона–Лейбница
 .
.
Некоторые тригонометрические формулы
 ;
;  ;
;  ;
;
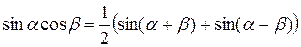 ;
; 
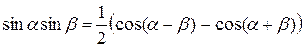
Задача 1. Вычислить интеграл  .
.
Решение. Воспользуемся основными свойствами неопределенного интеграла (прил. 2) и представим данный интеграл в виде суммы интегралов, для которых применим формулу (2), (1) и (3) из таблицы интегралов (прил. 3)

 .
.
Задача 2. Вычислить интеграл  .
.
Решение. Данный интеграл является определенным. Для его вычисления необходимо воспользоваться формулой Ньютона–Лейбница (19)
|
|
|
 .
.
Тогда в соответствии с формулой (2) (прил. 3) имеем


 .
.
Задача 3. Вычислить интеграл  .
.
Решение. Интеграл можно свести к табличному (7), если сделать замену 3 х = t. Дифференцируя обе части равенства, получим 3dх = dt, т.е.  . Так как интеграл определенный, необходимо изменить пределы интегрирования: если х = 1, то t = 3; если х = 3, то t = 9. Следовательно,
. Так как интеграл определенный, необходимо изменить пределы интегрирования: если х = 1, то t = 3; если х = 3, то t = 9. Следовательно,
 =
= 
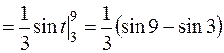 .
.
Задача 4. Вычислить интеграл  .
.
Решение. Интеграл можно свести к табличному (3), если аналогично задаче 3, сделать замену t = 5 х – 1
 .
.
Задача 5. Вычислить интеграл 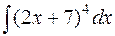 .
.
Решение. Интеграл можно свести к табличному (2), если аналогично задаче 3, сделать замену t = 2 х + 7

 .
.
Задача 6. Вычислить интеграл  .
.
Решение. Интеграл можно свести к табличному (9), если сделать замену t = х / 5
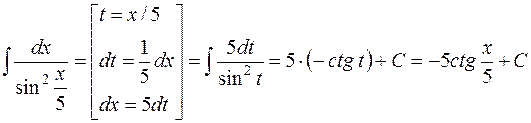 .
.
Задача 7. Вычислить интеграл  .
.
Решение. Интеграл можно свести к табличному (4), если сделать замену t = 6 х. Так как интеграл определенный, необходимо сменить пределы интегрирования
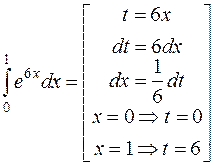 =
= 
 .
.
Задача 8. Вычислить интеграл  .
.
Обозначим  Найдем
Найдем 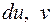
 .
.
Тогда

 .
.
Задача 9. Вычислить интеграл  .
.
Положим
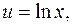

Тогда
 .
.
Получаем

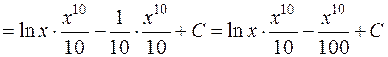 .
.
Задача 10. Вычислить интеграл  .
.
Решение. Для определенного интеграла также применима формула по частям

В качестве u (x) выберем 4 х – 3 (см. задачу 8), тогда  . Найдем
. Найдем
 и
и  .
.
Тогда


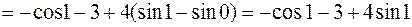 .
.
Задача 11. Вычислить интеграл  .
.
Решение. Это интеграл вычисляется с помощью формул тригонометрии (прил. 4). Воспользуемся формулой понижения степени
 , получим
, получим
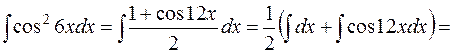
 .
.
Задача 12. Вычислить  .
.
Решение. Применяя тригонометрическую формулу
 , получим
, получим

 .
.
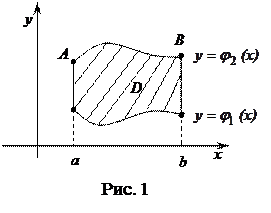 Задача 13. Вычислить площадь области D, ограниченной линиями
Задача 13. Вычислить площадь области D, ограниченной линиями  , y = x – 1, x = 0, x = 2.
, y = x – 1, x = 0, x = 2.
Решение. Площадь области D, ограниченной линиями  ,
,  , x = а, x = b (рис. 1), вычисляется по формуле
, x = а, x = b (рис. 1), вычисляется по формуле

 .
.
Построим заданную область D, ограниченную линиями  , y = x – 1, x = 0, x = 2 (рис. 2). Сверху область ограничивает парабола
, y = x – 1, x = 0, x = 2 (рис. 2). Сверху область ограничивает парабола  , т.е.
, т.е. 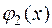 = x 2, снизу – прямая y = x –1, т.е.
= x 2, снизу – прямая y = x –1, т.е.  = x –1.
= x –1.
Подставляя все данные в формулу, найдем площадь области
|
|
|

 (кв. ед.)
(кв. ед.)

Задача 14. Вычислить площадь области D, ограниченной линиями 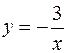 , y = 0, x = 1, x = 3.
, y = 0, x = 1, x = 3.
Решение. Построим заданную область D, ограниченную линиями 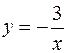 , y = 0, x = 1, x = 3 (рис. 3). Сверху область ограничивает прямая y = 0, т.е.
, y = 0, x = 1, x = 3 (рис. 3). Сверху область ограничивает прямая y = 0, т.е. 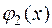 = 0, снизу – гипербола
= 0, снизу – гипербола 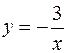 , т.е.
, т.е.  .
.
Подставляя все данные в формулу, найдем площадь области
 3 ln 3 (кв. ед.)
3 ln 3 (кв. ед.)
Дифференциальные уравнения
Дифференциальные уравнения – это уравнения, содержащие производные некоторой функции. Простым, но очень важным является случай, когда в данном уравнении можно разделить переменные, т.е. с помощью преобразований сделать так, чтобы в одной части было выражение, зависящее только от х, а в другой – от у. Такие уравнения называются дифференциальными уравнениями с разделяющимися переменными.
Линейное дифференциальное уравнение первого порядка

решается методом Бернулли с помощью подстановки
 ,
,  .
.
При решении однородного линейного дифференциального уравнения второго порядка с постоянными коэффициентами

составляется характеристическое уравнение
 .
.
При этом общее решение имеет вид
1)  , если корни k 1и k 2действительны и различны (
, если корни k 1и k 2действительны и различны ( );
);
2)  , если корни k 1и k 2 действительны и равны (k 1= k 2 = k) (корень кратности 2);
, если корни k 1и k 2 действительны и равны (k 1= k 2 = k) (корень кратности 2);
3)  , если корни комплексные
, если корни комплексные  .
.
Задача 27. Найти общее решение дифференциального уравнения
 .
.
Решение. Перепишем уравнение, используя другое обозначение для производной  ,
,
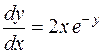 .
.
Разделим переменные, умножив уравнение на выражение  . Это приведет к равенству
. Это приведет к равенству
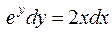 .
.
Проинтегрируем обе части полученного уравнения
 ,
,
вычислим интегралы с помощью формул (4) и (2) из прил. 3

и выразим у  .
.
Получившееся выражение называется общим решением дифференциального уравнения.
Задача 28. Найти общее решение дифференциального уравнения
 .
.
Решение. Данное дифференциальное уравнение также относится к уравнениям с разделяющимися переменными и решается аналогично задаче 27. Перепишем уравнение в виде
 .
.
Разделим переменные, умножив обе части уравнения на  ,
,
 .
.
В результате вычисления интегралов (формулы (16) и (8) из прил. 3)

получим общее решение дифференциального уравнения
 .
.
Задача 29. Найти общее решение дифференциального уравнения
 .
.
Решение. Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям первого порядка, имеющим вид
|
|
|
 .
.
Такое уравнение можно решать методом Бернулли с помощью подстановки
 ,
,
где u (x) и v (x) – две неизвестные функции. Подставляя в исходное уравнение
 и
и  ,
,
получим
 или
или  .
.
Так как одна из неизвестных функций может быть выбрана произвольно, возьмем в качестве v одно из частных решений уравнения
 .
.
При этом исходное дифференциальное уравнение примет вид
 .
.
Рассмотрим каждое из получившихся уравнений. Первое уравнение – дифференциальное уравнение с разделяющимися переменными. Разделяем переменные
 ,
,
 ,
,  .
.
Интегрируя, находим
 ,
,
 или
или  .
.
Подставим найденную функцию v во второе уравнение  . Получим
. Получим
 , откуда
, откуда  .
.
Это дифференциальное уравнение с разделяющимися переменными. Решая его, находим функцию и
 ,
,  ,
,
 ,
,  .
.
Возвращаясь к функции у, получим общее решение исходного дифференциального уравнения
 .
.
Задача 31. Найти общее решение уравнения  .
.
Решение. Данное дифференциальное уравнение относится к однородным линейным дифференциальным уравнениям второго порядка с постоянными коэффициентами
 .
.
Если заменить в дифференциальном уравнении  на k 2,
на k 2,  – на k, y – на 1, получим алгебраическое уравнение
– на k, y – на 1, получим алгебраическое уравнение
 ,
,
которое называется характеристическим уравнением однородного уравнения. Характеристическое уравнение есть уравнение второй степени и имеет два корня. Обозначим их через k 1и k 2. Возможны три случая.
1) Корни k 1и k 2– действительные и различные ( ).В этом случае общее решение уравнения будет
).В этом случае общее решение уравнения будет
 .
.
2) Корни k 1и k 2 –действительные и равные (k 1= k 2 = k).В этом случае общее решение уравнения будет
 или
или  .
.
3) Корни  и
и  – комплексные, т.е. дискриминант квадратного уравнения D < 0. Общее решение уравнения в этом случае будет иметь вид
– комплексные, т.е. дискриминант квадратного уравнения D < 0. Общее решение уравнения в этом случае будет иметь вид
 .
.
Составим характеристическое уравнение исходного уравнения
 .
.
Оно имеет два различных действительных корня k 1= 1 и k 2 = 2 (случай 1). Поэтому общее решение будет записано в виде
 .
.
Задача 32. Найти общее решение уравнения  .
.
Решение. Согласно теории, изложенной в задаче 31, составим характеристическое уравнение
|
|
|
 .
.
Оно имеет два равных корня k 1= k 2 = 3 (случай 2). Поэтому общее решение есть
 .
.
Задача 33. Найти общее решение уравнения  .
.
Решение. Согласно теории, изложенной в задаче 31, составим характеристическое уравнение
 .
.
Дискриминант этого уравнения отрицательный
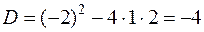 ,
,  .
.
Значит, уравнение имеет комплексные корни
 ,
,
т.е. 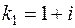 ,
,  , где
, где  ,
,  (случай 3). Поэтому общее решение есть
(случай 3). Поэтому общее решение есть
 .
.
Задача 34. Найти общее решение уравнения  .
.
Решение. Согласно теории, изложенной в задаче 31, составим характеристическое уравнение
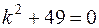 ,
,  ,
,
т.е. уравнение имеет комплексные корни  ,
,  , где
, где 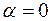 ,
,  (случай 3). Поэтому общее решение есть
(случай 3). Поэтому общее решение есть
 .
.
Задача 35. Найти общее решение дифференциального уравнения
 .
.
Решение. Данное уравнение является линейным однородным дифференциальным уравнением 3 порядка с постоянными коэффициентами. Составим характеристическое уравнение (см. задачу 31)
 ,
,
 ,
,
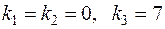 .
.
Паре корней  соответствует решение
соответствует решение

Корню  соответствует решение
соответствует решение
 .
.
Общее решение исходного уравнения есть сумма полученных решений  .
.
Задача 36. Найти частное решение дифференциального уравнения  , удовлетворяющее условиям
, удовлетворяющее условиям  ,
,  .
.
Решение. Дифференциальное уравнение второго порядка,разрешенное относительно у", имеет вид
 .
.
В результате двукратного последовательного интегрирования получаем общее решение этого уравнения
 .
.
Проинтегрируем исходное уравнение
 .
.
Выполним замену 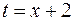 и вычислим интеграл
и вычислим интеграл
 .
.
Подставив начальное условие  , найдем константу С 1
, найдем константу С 1
 ,
,  .
.
Тогда уравнение примет вид
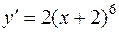 .
.
Еще раз проинтегрируем полученное уравнение и вычислим интеграл, выполнив замену 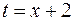 , получим
, получим
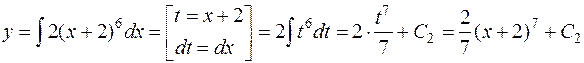 .
.
Подставив начальное условие  , найдем константу С 2
, найдем константу С 2
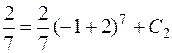 ,
,  .
.
Значит, частное решение дифференциального уравнения имеет вид  .
.
Задача 37. Найти частное решение уравнения  при начальных условиях
при начальных условиях  ,
,  .
.
Решение. Данное дифференциальное уравнение решается аналогично задаче 36. Проинтегрируем его
 .
.
Вычислим интеграл с помощью замены 
 .
.
Подставив начальное условие  , найдем константу С 1
, найдем константу С 1
 ,
,  .
.
Тогда уравнение примет вид
 .
.
Еще раз проинтегрируем полученное уравнение и вычислим интеграл, выполнив замену  , получим
, получим
 .
.
Подставив начальное условие  , найдем константу С 2
, найдем константу С 2
 ,
,  .
.
Значит, частное решение дифференциального уравнения имеет вид
 .
.
Ряды
Необходимый признак сходимости ряда: Для сходимости ряда необходимо, чтобы
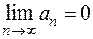 .
.
Радикальный признак Коши: Если существует предел
 ,
,
где b – обозначение найденного предела, тогда
1) если b < 1, ряд сходится;
2) если b > 1, ряд расходится;
3) если b =1, рассматриваемый признак не дает ответа на вопрос о сходимости ряда.
Признак Даламбера: Если существует предел
|
|
|
 ,
,
где b – обозначение найденного предела, тогда
1) если b < 1, ряд сходится;
2) если b > 1, ряд расходится;
3) если b =1, рассматриваемый признак не дает ответа на вопрос о сходимости ряда.
Предельный признак сравнения: Если существует конечный и отличный от нуля предел  то положительные ряды
то положительные ряды  и
и  одинаковы в смысле сходимости.
одинаковы в смысле сходимости.
Обобщенный гармонический ряд – ряд вида  , где
, где  – действительное число, сходится, если
– действительное число, сходится, если  , и расходится, если
, и расходится, если 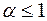 .
.
Признак Лейбница для знакочередующихся рядов  : Если для ряда выполняются два условия:
: Если для ряда выполняются два условия:
1) члены ряда монотонно убывают
 , (n = 1, 2, 3…);
, (n = 1, 2, 3…);
2)общий член ряда стремится к нулю
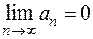 ,
,
то ряд сходится.
Задача 15. Исследовать на сходимость ряд  .
.
Решение. Необходимый признак сходимости ряда гласит: для сходимости ряда необходимо, чтобы 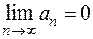 . Здесь
. Здесь  . Рассмотрим предел
. Рассмотрим предел
 .
.
Предел не равен нулю, следовательно, ряд расходится.
Задача 16. Исследовать на сходимость ряд  .
.
Решение. Используем радикальный признак Коши: если существует предел
 ,
,
где b – обозначение найденного предела, тогда
1) если b < 1, ряд сходится;
2) если b > 1, ряд расходится;
3) если b =1, рассматриваемый признак не дает ответа на вопрос о сходимости ряда.
Найдем предел

 .
.
Найденный предел b > 1. Следовательно, данный ряд расходится.
Задача 17. Исследовать на сходимость ряд  .
.
Решение. Используем признак Даламбера: если существует предел
 ,
,
где b – обозначение найденного предела, тогда
1) если b < 1, ряд сходится;
2) если b > 1, ряд расходится;
3) если b =1, рассматриваемый признак не дает ответа на вопрос о сходимости ряда.
Здесь  ,
,  , тогда имеем
, тогда имеем

 .
.
Найденный предел b < 1. Следовательно, данный ряд сходится.
Задача 18. Исследовать на сходимость ряд  .
.
Решение. Здесь  ,
,  , тогда по признаку Даламбера
, тогда по признаку Даламбера

 .
.
Найденный предел b > 1. Следовательно, данный ряд расходится.
Задача 19. Исследовать на сходимость ряд  .
.
Решение. Обобщенным гармоническим рядом называется ряд вида  , где
, где  – действительное число. Он ведет себя следующим образом:
– действительное число. Он ведет себя следующим образом:
1) сходится, если  ;
;
2) расходится, если 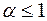 .
.
Так как в исходном примере  , то ряд сходится.
, то ряд сходится.
Задача 20. Исследовать на сходимость ряд  .
.
Решение. При исследовании сходимости ряда  можно воспользоваться предельным признаком сравнения положительных рядов: если существует конечный и отличный от нуля предел
можно воспользоваться предельным признаком сравнения положительных рядов: если существует конечный и отличный от нуля предел  то положительные ряды
то положительные ряды  и
и  одинаковы в смысле сходимости.
одинаковы в смысле сходимости.
Для сравнения возьмем обобщенный гармонический ряд  . При
. При 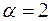 получим сходящийся ряд
получим сходящийся ряд  . Применим предельный признак сравнения
. Применим предельный признак сравнения
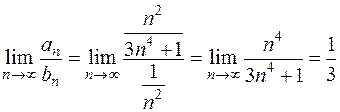 .
.
Так как предел конечен и отличен от нуля, то ряд  также сходится.
также сходится.
Задача 21. Исследовать на сходимость ряд  .
.
Решение. Этот ряд относится к знакочередующимся рядам вида
 ,
,
где  (n = 1, 2, 3…).
(n = 1, 2, 3…).
Применим к нему признак Лейбница: если для ряда выполняются два условия:
1) члены ряда монотонно убывают
 , (n = 1, 2, 3…);
, (n = 1, 2, 3…);
2)общий член ряда стремится к нулю
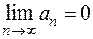 ,
,
то ряд сходится.
Для данного ряда условия теоремы выполнены
1)  ; 2)
; 2)  .
.
Следовательно, ряд  сходится.
сходится.
Если знакопеременный ряд сходится, то эта сходимость называется абсолютной или условной в зависимости от того, сходится или расходится соответствующий ряд из абсолютных величин членов знакопеременного ряда.
Если сходится ряд  , составленный из модулей, то соответствующий ряд
, составленный из модулей, то соответствующий ряд  называется абсолютно сходящим ся. Может оказаться, что ряд
называется абсолютно сходящим ся. Может оказаться, что ряд  расходится, а ряд
расходится, а ряд  сходится. В этом случае ряд
сходится. В этом случае ряд  называется условно сходящимся.
называется условно сходящимся.
Итак, рассмотрим ряд, составленный из абсолютных величин членов данного ряда
 =
=  .
.
Исследуем его на сходимость по признаку Даламбера
 .
.
Тогда ряд  сходится, следовательно, ряд
сходится, следовательно, ряд  сходится абсолютно.
сходится абсолютно.
Задача 22. Исследовать на сходимость ряд  .
.
Решение. Для данного ряда условия признака Лейбница выполняются:
1)  2)
2)  .
.
Значит, ряд сходится. Исследуя ряд на абсолютную сходимость, составим ряд из модулей
 .
.
Для исследования этого ряда на сходимость применим предельный признак сравнения. Для сравнения возьмем обобщенный гармонический ряд  . При
. При  получим расходящийся ряд
получим расходящийся ряд  . Применим предельный признак сравнения
. Применим предельный признак сравнения
 .
.
Так как предел конечен и отличен от нуля, то ряды  и
и  ведут себя одинаково в смысле сходимости, т.е. ряд
ведут себя одинаково в смысле сходимости, т.е. ряд  тоже расходится.
тоже расходится.
Так как ряд  расходится, следовательно, ряд
расходится, следовательно, ряд  сходится условно.
сходится условно.
Задача 23. Исследовать на сходимость ряд  .
.
Решение. Рассмотрим выполнение условий признака Лейбница для данного ряда
1)  .
.
Так как уже первое условие не выполняется, следовательно, ряд  расходится.
расходится.
Задача 24. Исследовать на сходимость ряд  .
.
Решение. Ряд вида
 ,
,
где а 0, а 1, а 2, …, аn, …–постоянные вещественные числа, называется степенным рядом.
Для каждого степенного ряда существует положительное число R такое, что этот ряд абсолютно сходится при  и расходится при
и расходится при  . Число R называется радиусом сходимости рассматриваемого ряда, а интервал (– R, R) называется интервалом сходимости этого ряда.
. Число R называется радиусом сходимости рассматриваемого ряда, а интервал (– R, R) называется интервалом сходимости этого ряда.
На концах интервала сходимости (в точках х = – R и х = R) степенной ряд может сходиться или расходиться. Этот вопрос решается отдельно для каждого числового ряда, получающегося из степенного ряда в результате подстановки в него указанных значений.
Радиус сходимости R степенного ряда можно определить с помощью признака Даламбера или радикального признака Коши
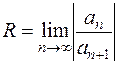 ,
,  .
.
Найдем радиус сходимости для заданного ряда по первой формуле. Так как
 ,
,  ,
,
получим

 .
.
Следовательно, R = 3. Поэтому данный ряд абсолютно сходится в интервале (– 3; 3) и расходится вне отрезка [– 3; 3].
Исследуем сходимость ряда в точках х = 3 и х = – 3.
При х = 3 исходный ряд принимает вид
 .
.
Это обобщенный гармонический ряд ( ) (задача 19). Значит, в этой точке заданный ряд расходится.
) (задача 19). Значит, в этой точке заданный ряд расходится.
При х = – 3 получаем знакочередующийся ряд
 .
.
Рассмотрим для него выполнение условий теоремы Лейбница (задача 21)
1)  ; 2)
; 2)  .
.
Условия выполняются, значит, ряд  сходится.
сходится.
Следовательно, область сходимости исходного ряда [– 3; 3).
Задача 25. Исследовать на сходимость ряд  .
.
Решение. В случае ряда  ,
,  ,
, 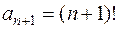
Тогда  . Значит, R= 0. Область сходимости
. Значит, R= 0. Область сходимости
– точка х = 0. Подставляя это значение в заданный ряд, получим нулевой
ряд 0 + 0 + 0 + …, который сходится (S = 0).
Следовательно, исходный ряд сходится только при х = 0.
Задача 26. Исследовать на сходимость ряд  .
.
Решение. Для ряда  .
.  ,
,  ,
,
 .
.
Следовательно,  . Значит, ряд сходится при любых х и область
. Значит, ряд сходится при любых х и область
сходимости ряда 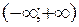 .
.
Приложение 1 Тренировочный тест
| № | Задания | Варианты ответов | ||||
| 1. | 
| 
| 
| 
| 
| 
|
| 2. | 
| 
| 
| 
| 
| 
|
| 3. | 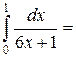
| 
| 
| 
| 
| 
|
| 4. | 
| 
| cos 5–cos 10 | 5(cos 5–cos 10) | 
| 5(cos 10–cos 5) |
| 5. | 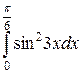 = =
| 
| 
| 
| ||
| 6. | 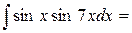
| 
| 
| 
| 
| 
|
| 7. |  = =
| 
| 
| 
| 
| 
|
| 8. | 
| 
| 
| 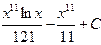
| 
| 
|
| 9. | 
| 
| 
| 
| 
| 
|
| 10. | Найти площадь области D,
ограниченной линиями:  . .
| 
| 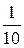
| 
| 
| 
|
| 11. | Найти площадь области D,
ограниченной линиями: 
| 
| 
| 
| 
| 
|
| 12. | Найти общее решение дифференциального уравнения
 . .
| 
| 
| 
| 
| 
|
| 13. | Найти общее решение дифференциального уравнения
 . .
| 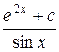
| 
| 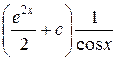
| 
| 
|
| 14. | Найти общий интеграл дифференциального уравнения
 . .
| 
| 
| 
| 
| 
|
| 15. | Найти общее решение дифференциального уравнения

| 
| 
| 
| 
| 
|
| 16. | Найти общее решение дифференциального уравнения

| 
| 
| 
| 
| 
|
| 17. | Найти общее решение дифференциального уравнения

| 
| 
| 
| 
| 
|
| 18. | Найти общее решение дифференциального уравнения 
| 
| 
| 
| 
| 
|
| 19. | Найти частное решение дифференциального уравнения 
|  e3 x e3 x
| 3e3 x | |||
|
|
|


