Необходимый признак сходимости числового ряда.

Лекция 45. Положительные числовые ряды. Признаки сходимости: сравнения, Даламбера, Коши.

В данной лекции мы обсудим следующий интересный и важный для практики вопрос: существует ли суммы бесконечного числа слагаемых? И если существуют, то как их найти?

Вспомним, что с суммой бесконечного числа слагаемых мы уже встречались ранее при рассмотрении определенных интегралов. Но там были специфические суммы – суммы бесконечно малых слагаемых. Здесь же рассмотрим суммы бесконечного числа слагаемых, когда слагаемые произвольны.

Числовые ряды

Определение. Выражение вида

(1)

представляющее собой сумму бесконечного числа слагаемых, называется рядом. Если слагаемые (члены) ряда (а₁; а₂; а₃; …) – числа, то ряд называется числовым. А если они являются функциями, то ряд является функциональным. В этой лекции мы будем рассматривать лишь числовые ряды.

Ключевым понятием любого ряда (1) является его сумма, то есть сумма всех тех слагаемых, которые содержатся в ряде. Так как в нем бесконечное число слагаемых, то его сумму нельзя получить прямым сложением всех слагаемых – так, как мы это делаем при складывании конечного числа слагаемых. Действительно, процесс суммирования членов ряда не будет иметь конца, и мы, таким образом, сумму ряда никогда не найдем. Поэтому и к определению, и к нахождению суммы ряда должен быть применен какой-то другой подход.

И этот подход состоит в следующем. Пусть

S_n = а₁+ а₂ + …+ а_n (2)

- сумма первых n слагаемых ряда (1), которую называют n -ой частичной суммой ряда. В частности,

S₁=a₁; S₂=a₁+a₂; S₃=a₁+a₂+a₃; … (3)

С изменением n будет меняться и частичная сумма S_n, причем при увеличении n она будет включать в себя все больше и больше слагаемых ряда (1). Тогда сумму всего этого ряда естественно определить как предел суммы S_n при . То есть, по определению,

(4)

- сумма ряда (1). В обозначении S_∞ суммы ряда значок ¥ указывает на то, что речь идет о сумме бесконечного числа слагаемых. Впрочем, этот значок обычно опускают и сумму ряда обозначают просто символом S.

Сумма ряда S_∞, как и всякий предел, может существовать, а может и не существовать, может быть бесконечной, а может быть и конечной. Если сумма ряда существует и конечна, ряд называется сходящимся. А если эта сумма равна ∞ или она не существует вообще, то ряд называется расходящимся.

Имеются способы (о них мы будем говорить ниже) выяснения вопроса о том, сходится или расходится данный числовой ряд. Если удалось установить, что ряд сходится, то у него есть конечная сумма S. Иногда её можно найти точно. Но чаще – только приближенно по формуле

S = S_∞ ≈ S_n,(5)

где S_n (см. (2)) – сумма первых n слагаемых ряда. Смысл формулы (5) состоит в том, что при нахождении суммы сходящегося ряда суммируется лишь некоторая часть его слагаемых (первые n слагаемых), а остальные просто отбрасываются. Результат будет получаться тем точнее, чем больше n. Есть и возможность оценки погрешности, допускаемой при замене S = S_∞ на S_n.

Пример 1. Показать, что ряд

0,9 + 0,09 + 0,009 + 0,0009 + … (6)

сходится и имеет сумму S = 1.

Решение. Для данного ряда имеем:

S₁ = 0,9; S₂ = 0,9 + 0,09 = 0,99; S₃ = 0,9 + 0,09 + 0,009 = 0,999; …

S_n = при .

Таким образом,

= 1. (7)

Как оказалось, сумма S ряда - число, поэтому ряд сходится. И так как эта сумма равна 1, то можем записать:

0,9 + 0,09 + 0,009 + 0,0009 + … = 1 (8)

Пример 2. Показать, что ряд

² = 1² + 2² + 3² + 4² + … (9)

расходится.

Решение. Очевидно, что для данного ряда

S_n = 1² + 2² + 3² + … + n ² ® ∞ при n ® ∞.

То есть

=¥ (10)

А значит, ряд (9) расходится, ибо его сумма бесконечна:

1² + 2² + 3² + 4² + … = ∞ (11)

Пример 3. Показать, что ряд

1 – 1 + 1 – 1 + 1 – … (12)

расходится.

Решение. Для данного ряда

S ₁ = 1; S ₂ = 1–1 = 0; S ₃ = 1–1+1 = 1; S ₄ = 1–1+1–1 = 0; …

То есть (13)

Очевидно, что - не существует (сумма ряда не существует). А значит, ряд расходится.

Пример 4. Рассмотрим числовой ряд вида

(14)

Этот ряд известен еще из курса элементарной математики под названием «сумма бесконечной геометрической прогрессии со знаменателем ». Как известно, эта сумма существует и конечна (а, значит, ряд (14) сходится) лишь при знаменателе прогрессии – 1 < q < 1, причем

= (– 1 < q < 1) (15)

При ряд (14) расходится, так конечной суммы не имеет.

 

Свойства числовых рядов

а). Отбрасывание у ряда конечного числа его членов или, наоборот, добавление к ряду конечного числа новых слагаемых не влияет на его сходимость - расходимость (а влияет только на величину его суммы, если она существует и конечна).

б). Если

то

.

То есть умножение (деление) всех членов ряда на некоторое число С не влияет на его сходимость – расходимость, а влияет только на его сумму, которая увеличивается (уменьшается) в соответствующее число раз (в С раз).

в). Если ряды и сходятся, причем и , то и ряд сходится, причем .

 

Необходимый признак сходимости числового ряда.

Теорема 1. Для сходимости любого числового ряда (1) необходимо, чтобы a_n ®0 при n ®∞, то есть чтобы .

Доказательство. Допустим, что ряд (1) сходится. Это значит, что существует и конечна его сумма S _∞, которая определяется пределом (4). Учитывая, что , откуда следует, что , получаем:

То есть действительно a_n ®0 при n ®∞. Теорема доказана.

Из доказанной теоремы следует, что если a_n не стремится к нулю при n® ∞, то ряд сходиться не может – он заведомо расходится.

Примечание. Условие a_n ®0 при n ®∞ является необходимым, но не достаточным условием сходимости числового ряда (1). Это значит, что оно еще не гарантирует сходимости ряда. Иначе говоря, возможна ситуация, когда при a_n ®0 при n ®∞, и тем не менее ряд (1) расходится.

Классическим примером такого ряда является гармонический ряд

(16)

Необходимое условие сходимости при n ®∞ для этого ряда очевидным образом выполняется. И тем не менее этот ряд расходится, так как его сумма S= ∞.

Докажем это. Для этого рассмотрим рис.1. На этом рисунке изображена бесконечно протяженная в горизонтальном направлении ступенчатая фигура, состоящая из заштрихованных прямоугольников, площади которых соответственно равны ( …). То есть суммарная площадь S этой заштрихованной фигуры как раз равна сумме S гармонического ряда (16). Но эта площадь S заведомо больше площади S₀ между осью ох и гиперболой в пределах для х от 1 до ¥. А

.

И так как S > S₀, то и S = ∞. Таким образом, гармонический ряд расходится, ибо его сумма S равна ∞:

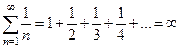(17)

 

12Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: