Составьте полную и упрощенную структурные схемы ИДПТЯУ.

Рис.2.42.1

Рис.2.42.2

Структурные схемы динамических систем, как известно, составляются, исходя из операторных уравнений этих систем.

Операторные уравнения динамических систем получают путём преобразования по Лапласу дифференциальных уравнений этих систем.

Рассмотрим процедуру составления операторных уравнений на примере ИДПТЯУ. Исходная система дифференциальных уравнений ИДПТЯУ, указанная в ответе к вопросу 2.41, имеет вид:

 

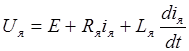, (1)

 

, (2)

 

, (3)

 

. (4)

 

Далее исходную систему уравнений (1)-(4) необходимо преобразовать по Лапласу, то есть обе части уравнений умножить на функцию 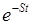, где S – оператор Лапласа (комплексное число); t – время, а затем проинтегрировать обе части уравнений по времени в пределах от нуля до бесконечности. Тогда получим операторные уравнения ИДПТЯУ:

 

, (5)

 

, (6)

 

, (7)

 

, (8)

 

где 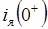, - начальные значения тока якоря и угловой скорости вращения якоря в момент времени «ноль - плюс», то есть в положительный момент времени, бесконечно близкий к нулю.

Учёт начальных значений приводит к громоздким структурным схемам. Поэтому желательно начальные значения исключить. Для этого поступают так. Допускают, что в отрицательные моменты времени, то есть до изменения входных величин (в нашем случае – это величина и ) система находится в покое. Это означает, что все производные в уравнениях (1)-(7) в отрицательные моменты времени равны нулю, включая также момент «ноль – минус» (), то есть в отрицательный бесконечно близкий к нулю момент времени. Тогда для этого момента уравнения (1) – (4) примут вид:

 

, (9)

 

, (10)

 

, (11)

 

. (12)

 

Далее действуем так. Вычтем из уравнения (1) уравнение (9) и в результате получим:

 

. (13)

 

Так как , то справедливо

 

. (14)

 

Уравнение (13) с учётом (14) примет вид:

 

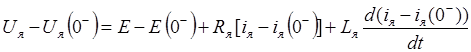. (15)

 

Введём обозначения:

 

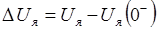, (16)

 

, (17)

 

. (18)

 

С учётом обозначений (16) – (18) уравнение (15) примет вид;

 

. (19)

 

Это уравнение называют уравнением в приращениях.

Заметим далее, что

 

, (20)

 

поскольку, как известно из электротехники, ток, протекающий через индуктивность, не может измениться скачком. Поэтому в силу (18) и (20) получим:

 

, (21)

 

то есть начальное значение величины равно нулю.

Уравнение (19), преобразованное по Лапласу, при нулевом начальном значении величины примет вид:

 

, (22)

 

то есть при указанных допущениях (состояние покоя динамической системы до подачи воздействий и отсутствие скачка у переменной 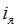, которая входит под знак производной) структура уравнения (22) оказывается более простой, чем у подобного ему уравнения (5). Это позволяет соответственно построить и более простую структурную схему системы. Уравнение (22) называют операторным уравнением в приращениях.

Приводя аналогичные рассуждения для уравнений (6) – (8) и вводя приращения

 

, (23)

 

, (24)

 

, (25)

а также учитывая, что угловая скорость якоря не может измениться скачком, то есть , и следовательно, начальное значение величины 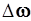является нулевым: , приходим к следующим операторным уравнениям в приращениях:

 

, (26)

 

, (27)

 

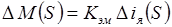, (28)

 

Итак, операторные уравнения в приращениях (22), (26) – (28), описывают динамические процессы в ИДПТЯУ. Опираясь на эти уравнения можно построить структурную схему ИДПТЯУ.

Построение структурной схемы начинают, как правило, с определения выходной величины системы. В нашем случае выходной величиной будем считать приращение угловой скорости и определим её, используя, например, уравнение (27). Откуда (опустим далее оператор Лапласа S):

 

(29)

 

Уравнение (29) соответствует пропорциональному звену с коэффициентом передачи 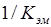и отображается графически прямоугольником с двумя стрелками: входной, под которой помещают входную величину , и выходной, под которой указывают выходную величину (рис. 2.42.1). Внутрь прямоугольника помещают значение коэффициента передачи 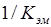. Из рисунка видно, что теперь следует определить величину . Для определения величины выполним следующие преобразования.

Выразим явно из (26) величину :

 

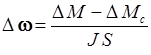(30)

 

Домножим левую и правую части равенства (30) на величину и, учитывая равенство (27), получим:

 

. (31)

 

Умножая и деля правую часть равенства (31) на величину , а также учитывая равенство (28), после преобразований получим:

 

. (32)

 

Умножая и деля второе слагаемое на величину и вводя обозначение

 

, (33)

 

получим после преобразований:

 

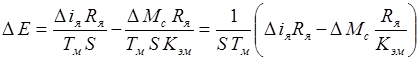. (34)

 

Заметим, что величина имеет размерность времени и называется электромеханической постоянной времени двигателя постоянного тока. Физический смысл величины рассматривается далее.

Возвращаясь к равенству (34), отметим, что это равенство графически означает, что для получения искомой величины необходимо из величины вычесть величину , а затем преобразовать через интегратор с постоянной времени , то есть для реализации равенства (34) необходимо последовательно соединённые вычитатель и интегратор, что отражено на рис. 2.42.1

Из этого рисунка видно, что для определения величины необходимо знать величины и . Последняя величина является известной, поскольку приращение момента сопротивления является возмущением и считается заданной величиной. Величина может быть определена так. Перенося величину в левой части равенства (22) и вынося в правой части величину за скобки, получим:

 

. (35)

Вводя обозначение , перепишем (35) в виде:

 

.

 

Заметим, что величина 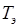имеет размерность времени и называется электромагнитной постоянной времени двигателя постоянного тока. Итак, для получения величины необходимо иметь последовательно соединённые вычитатель (для определения разности величин и ) и апериодическое звено с единичным коэффициентом передачи и постоянной времени 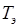, что отображено на рис. 2.42.1. Величина является входной заданной величиной, а величину можно взять на выходе интегратора, организуя обратную отрицательную связь по величине .

Нетрудно видеть, что на структурной схеме после указанных построений не осталось неизвестных (неопределённых величин), в связи с чем построение структурной схемы ИДПТЯУ оказывается законченным.

Перейдём к построению упрощенной структурной схемы ИДПТЯУ. В большинстве двигателей приращение угловой скорости 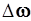является более инерционной величиной, чем приращение тока якоря .

Как видно из схемы (рис. 2.42.), приращение ЭДС прямо пропорционально связано с величиной 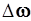и поэтому также является более инерционной величиной, чем приращение тока . Это означает, что приращение ЭДС в динамических, переходных режимах работы ИДПТЯУ (при условии малых отклонений от некоторого установившегося режима работы) может быть принято равным нулю, то есть обратная связь по ЭДС как бы отсутствует. Поэтому структурная схема ИДПТЯУ может быть упрощена путём отбрасывания обратной связи по приращению ЭДС и приведена к виду, представленному на рис.2.42.2.

В ряде случаев при синтезе регуляторов тех систем автоматического управления, которые содержат ИДПТЯУ, с целью упрощения соотношений считают, что приращение возмущения . Тогда структурная схема ИДПТЯУ ещё более упрощается и приобретает вид, представленный на рис. 2.42.3.

Рис.2.42.3

 

Заметим, что в литературе знак приращения , как правило, не указывается (по умолчанию) ни в уравнениях, ни на структурных схемах, по-видимому, с целью уменьшения громоздкости обозначений. Но специалист по автоматике должен ясно понимать, что если на структурных схемах или операторных уравнениях отсутствуют знаки приращений, то либо они отсутствуют по умолчанию, либо при анализе данных систем полагают, что начальные значения выходных величин динамических звеньев принимаются равными нулю.

 

⇐ Предыдущая12

Поделиться:

Воспользуйтесь поиском по сайту: