 |
Краткие теоретические сведения
|
|
|
|
Особое место среди цепей передачи электромагнитной энергии (или электрической мощности) занимают трансформаторы. Они представляют собой статические электромагнитные устройства, осуществляющие передачу электромагнитной энергии из одной части электрической цепи в другую посредством явления взаимной индукции. Конструктивно трансформаторы выполняются в виде нескольких (двух и более) обмоток катушек индуктивности, расположенных на едином сердечнике (как правило, из магнитодиэлектрика (альсифер, карбонильное железо, феррит) или диамагнетика (сталь, латунь и пр.)). Обмотка, подключаемая к источнику электромагнитной энергии, носит название первичной, а подключаемая к потребителю – вторичной [1]. Положительным свойством трансформатора является отсутствие гальванической связи между его первичной и вторичной обмотками.
Рассмотрим взаимодействие двух индуктивностей, расположенных в непосредственной близости друг к другу (рис. 8.1).
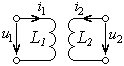
Рис. 8.1 – К рассмотрению взаимодействия двух близко расположенных индуктивностей
При протекании электрического тока через катушку индуктивности в пространстве ее окружающем образуется магнитное поле. Силовые линии такого поля замкнуты и охватывают витки данной катушки индуктивности (рис. 8.2).
Теоретически силовые линии магнитного поля пронизывают все бесконечное пространство. Однако величина магнитного поля, созданного током, протекающим через катушку индуктивности, уменьшается обратно пропорционально квадрату расстояния от нее.
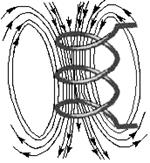
Рис 8.2 – Силовые линии магнитного поля катушки индуктивности, вызванного протеканием в ней электрического тока
Аналогично тому, как изменение магнитного потока, пронизывающего витки катушки приводит к наведению в ней ЭДС самоиндукции, происходит наведение ЭДС взаимной индукции во второй катушке, расположенной в непосредственной близости от первой. Такие катушки индуктивности, для которых характерно взаимное влияние токов, в них протекающих, друг на друга называются индуктивно связанными.
|
|
|
Величина магнитного потока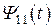 
, пронизывающего все витки первой катушки индуктивности, носит название потокосцепления самоиндукции и связана с величиной тока 
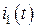, протекающего через нее, выражением:
, (8.1)
где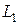 
- индуктивность первой катушки индуктивности.
Аналогично величину потока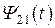 
, создаваемого первой катушкой индуктивности и пронизывающего ветки второй, называют потокосцеплением взаимной индукции и оно связано с величиной тока 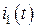его порождающего выражением вида:
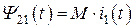, (8.2)
где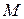 
- коэффициент взаимной индукции (взаимная индуктивность).
Если при этом вторая катушка индуктивности не работает в режиме холостого хода и по ней протекает ток, то она оказывает аналогичное воздействие на первую катушку. Величины потокосцепления самоиндукции и взаимной индукции для второй катушки индуктивности определяются аналогичными выражениями:
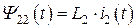, (8.3)
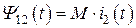, (8.4)
где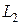 
- индуктивность второй катушки индуктивности. Величина взаимной индуктивности при этом остается той же.
В зависимости от взаимных направлений токов в индуктивно связанных элементах потокосцепления самоиндукции и взаимной индукции для обеих катушек индуктивности могут либо складываться, либо вычитаться. В первом случае говорят, что катушки индуктивности включены согласно, а во втором – встречно. Таким образом, полное потокосцепление с витками каждой из катушек индуктивности оказывается равным:
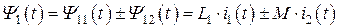, (8.5)
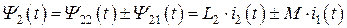, (8.6)
где знак «+» соответствует согласному включению, а знак «-» - встречному.
Тогда напряжения, возникающие на зажимах данных катушек индуктивности, оказываются равными:
|
|
|
, (8.7)
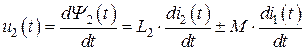. (8.8)
Чтобы отображать на схеме способ включения катушек индуктивности используют так называемые одноименные зажимы, изображаемые в виде жирных точек с одного из концов катушек индуктивности. Если при этом одноименные зажимы расположены таким образом, что токи в катушках индуктивности втекают в эти зажимы или вытекают из них с одной стороны, то катушки индуктивности включены согласно, а если нет – то встречно (рис. 8.3).
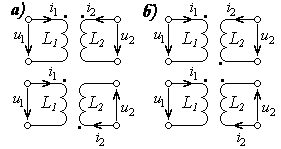
Рис 8.3 – Обозначение способа включения катушек индуктивности с помощью одноименных зажимов: а) согласное включение; б) встречное включение
Величина потокосцепления самоиндукции, в общем случае, состоит из двух частей. Одна часть описывает часть потока магнитного поля, который сцепляется как с витками первой, таки с витками второй катушки, а вторая – ту часть магнитного потока, которая цепляется только с витками первой катушки. Вторая часть потока носит название магнитного потока рассеяния. Таким образом:
, 
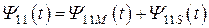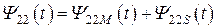, (8.9)
где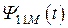 
и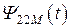 
- часть магнитного потока самоиндукции, сцепленного с витками обеих катушек индуктивности, а 
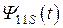и 
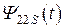- магнитные потоки рассеяния.
Величина взаимной индуктивности 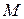, с одной стороны определяется потокосцеплением взаимной индукции 
(или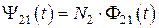 
), а с другой стороны потоки взаимной индукции определяются соответствующими частями потоков самоиндукци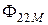и 
и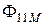 
, соответственно. Таким образом:
,
,
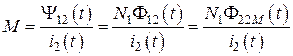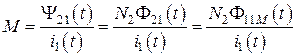и, следовательно, выполняется равенство
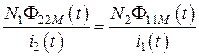. (8.10)
В случае так называемого идеального трансформатора, когда отсутствуют все виды потерь, включая магнитные потоки рассеяния,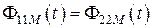 
и равенство (8.10) упрощается:
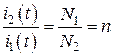, (8.11)
где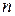 
- коэффициент трансформации. Учитывая, что индуктивность прямо пропорциональная квадрату числа витков, выражение для коэффициента трансформации можно переписать в виде:
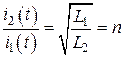. (8.12)
Чтобы выяснить, как при этом изменяются мгновенные значения напряжения достаточно воспользоваться выражениями (8.7) и (8.8):
,
.
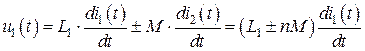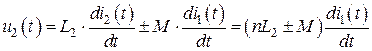Тогда:
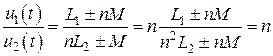. (8.13)
Выражения (8.11) – (8.13) описывают свойства идеального трансформатора. В частности из них следует, что идеальный трансформатор не меняет величины мгновенной мощности:
.
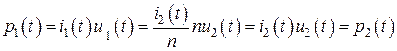Если величина коэффициента трансформации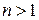 
, то трансформатор называют понижающим, а если 
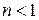- то повышающим.
|
|
|
Идеальный трансформатор на электрических схемах изображается так, как это показано на рис. 8.4.
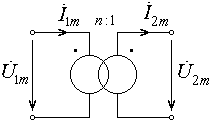
Рис. 8.4 – Графическое изображение идеального трансформатора
Отношение магнитного потока рассеяния к току, протекающему по катушке индуктивности, носит название индуктивности рассеяния:
, 
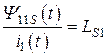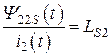. (8.14)
Пусть отсутствуют все виды потерь, включая магнитные потоки рассеяния. Тогда
Исходя из выражений (8.9) можно записать, что:
, (8.15)
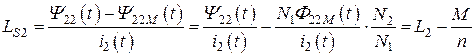. (8.16)
Чем меньше магнитные потоки рассеяния, тем эффективнее работает трансформатор. Эту эффективность можно оценить отношениями магнитных потоков вида:
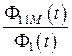и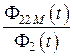 
,
которые показывают долю магнитного потока, создаваемого одной из катушек индуктивности и достигающего второй катушки индуктивности. Среднее геометрическое данных отношений носит название коэффициента связи катушек индуктивности:
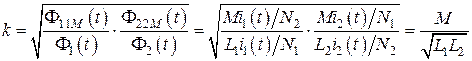. (8.17)
Коэффициент связи зависит от взаимной ориентации катушек индуктивности и максимален, если оси катушек индуктивности параллельны друг другу и увеличивается с уменьшением расстояния между ними. Если же оси катушек индуктивности образуют прямой угол, то связь между ними практически отсутствует и коэффициент связи близок к нулю.
С учетом выражения (8.17), выражения для индуктивностей рассеяния примут вид:
,
.
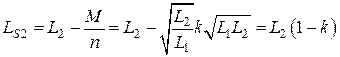Поскольку трансформатор обычно используют для преобразования уровней гармонического тока или напряжения, то логично перейти от мгновенных значений к их изображениям – комплексным мгновенным значениям:
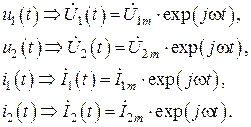(8.18)
Тогда выражения, описывающие работу идеального трансформатора, примут вид:
. (8.19)
Исходя из выражения (8.19) можно узнать, как связаны между собой входное и выходное сопротивления трансформатора, иначе говоря, узнать закон преобразования трансформатором величины сопротивления:
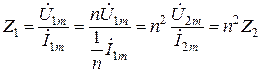. (8.20)
Свойство (8.20) идеального трансформатора может быть использовано для согласования сопротивлений источника преобразуемого сигнала и потребителя. Такой трансформатор носит название согласующего.
Реальный трансформатор отличается от идеального не только наличием магнитных потоков рассеяния, но также потерями энергии, связанными с омическими сопротивлениями обмоток, намагничиванием сердечника, наличием паразитной межвитковой емкости у каждой из обмоток и между ними и пр. Однако магнитные потоки рассеяния представляют собой наиболее значительную часть потерь энергии. Построим модель реального трансформатора, которая содержала бы в своем составе не только идеальный трансформатор, но и реальную часть, учитывающую данный вид потерь. Для этого осуществим переходы (8.18) в выражениях (8.7) и (8.8) для мгновенных значений напряжений на зажимах связанных катушек индуктивности:
|
|
|
,
,
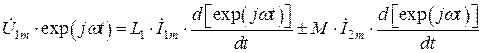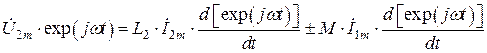или же
, 
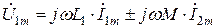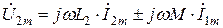. (8.21)
Выражениям (8.21) можно поставить в соответствие схему замещения без магнитных связей, если осуществить небольшое преобразование выражений:
(8.22)
причем верхний знак соответствует согласному включению катушек индуктивности, а нижний – встречному. Тогда соответствующая схема замещения примет вид, показанный на рис. 8.5. В дальнейшем будем рассматривать только согласное включение.
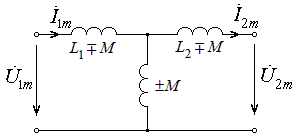
Рис. 8.5 – Схема замещения двух связанных катушек индуктивности
При преобразовании выражений (8.21) в правой части были добавлены и вычтены слагаемые вида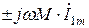 
и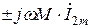 
. Результат не изменится, если умножить эти слагаемые на 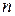. Однако схема замещения примет вид, приведенный на рис. 8.6. Индуктивност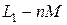и 
и 
, согласно выражениям (8.15) и (8.16) есть индуктивности рассеяния обмоток, а индуктивность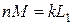 
носит название индуктивности намагничивания.
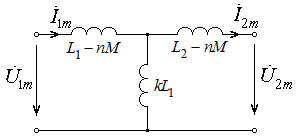
Рис. 8.6 – Схема замещения реального трансформатора
Представим реальный трансформатор схемой замещения, приведенной на рис. 8.7.
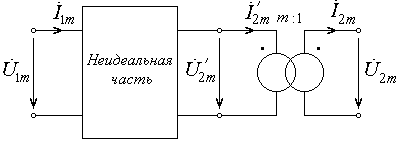
Рис. 8.7 – Схема замещения реального трансформатора с разделением на идеальную и неидеальную части
Тогда, учитывая свойства идеальной части можно переписать выражения (8.22) в виде:
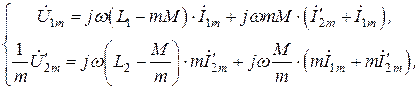
где в первом уравнении добавлено и вычтено слагаемое вида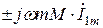 
, а во втором уравнении – вида 
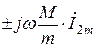и учтено, что 
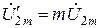и 
. После элементарных преобразований получаем:
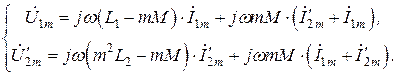(8.23)
Тогда схема замещения неидеальной части примет вид, приведенный на рис. 8.8.
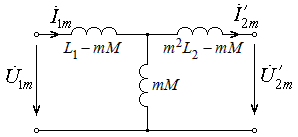
Рис. 2.8 – Схема замещения неидеальной части
Недостатком данной схемы замещения является наличие трех индуктивностей. Его можно избежать, если специальным образом подобрать коэффициент трансформации 
идеальной части. Действительно, выберем его так, чтобы первая из индуктивностей обратилась в ноль:
.
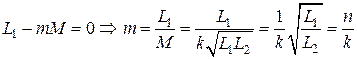Тогда оставшиеся индуктивности окажутся равными:
,
.
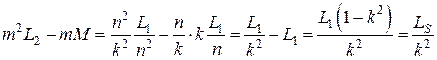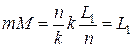Тогда схема замещения реального трансформатора принимает вид, показанный на рис. 8.9.
Входящая в схему замещения величина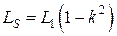 
носит название индуктивности рассеяния трансформатора. Если коэффициент связи 
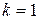, то магнитные потоки рассеяния отсутствуют и такой трансформатор называется совершенным. Схема замещения совершенного трансформатора представлена на рис. 8.10.
|
|
|
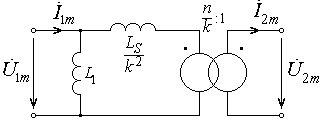
Рис. 8.9. – Схема замещения реального трансформатора
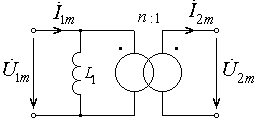
Рис. 8.10 – Схема замещения совершенного трансформатора
Из полученной схемы замещения видно, что совершенный трансформатор отличается от идеального наличием индуктивности 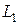. Таким образом перейти от совершенного трансформатора к идеальному можно, если устремить 
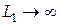. Тогда устранится последний вид потерь, связанный с наличием у совершенного трансформатора тока холостого хода. Но поскольку коэффициент трансформации и коэффициент связи должны остаться конечными, то индуктивность вторичной обмотки и взаимная индуктивность должны быть также бесконечными, т. е. 
и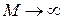 
.
Рассмотрим цепь, состоящую из генератора гармонического напряжения, реального трансформатора и нагрузки (рис. 8.11) и исследуем частотные свойства трансформатора. Будем полагать, что и генератор и нагрузка обладают активными сопротивлениями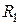 
и 
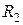, соответственно. В качестве передаточной функции, отражающей частотные свойства реального трансформатора, выберем коэффициент передачи мощности.
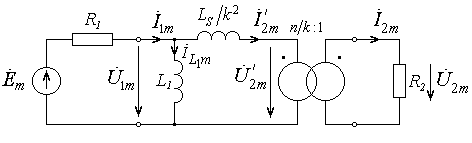
Рис. 8.11 – К определению коэффициента передачи мощности
Составим систему уравнений по законам Кирхгофа и Ома, а также воспользуемся свойствами идеального трансформатора:
(8.24)
Под коэффициентом передачи мощности будем понимать отношение активной мощности, развиваемой в нагрузке к номинальной мощности генератора:
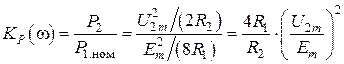. (8.25)
Таким образом, задача свелась к отысканию амплитуды напряжения на нагрузке. С этой целью исключим из системы уравнений (8.24) прочие неизвестные реакции. Для начала используем свойства идеального трансформатора. Тогда система примет вид:
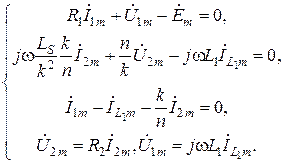
Следующим шагом с помощью закона Ома исключим токи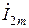 
и 
. Получим:
Выразим ток 
из последнего уравнения и подставим в первое. Тогда после простейших преобразований получим:
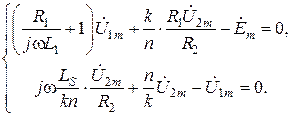
Окончательно исключим напряжение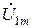 
, выразив его из второго уравнения и подставив в первое:
или же
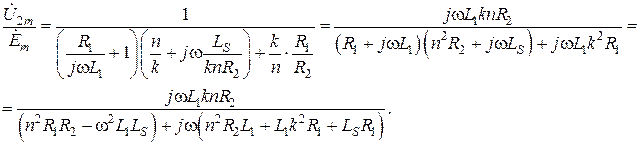
Тогда коэффициент передачи мощности:
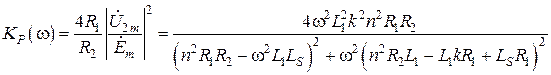.(8.26)
Чтобы проанализировать данное выражение разделим числитель и знаменатель дроби на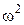 
. Получим:
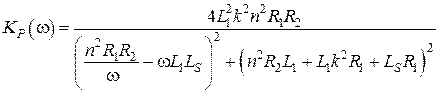. (8.27)
Из полученного выражения видно, что от частоты зависит одна единственная скобка, расположенная в знаменателе. Таким образом, дробь достигнет максимума на такой частоте, для которой данная скобка обратится в ноль. Назовем данную частоту центральной (средней). Тогда она оказывается равной:
. (8.28)
Соответствующее значение коэффициента передачи мощности оказывается равным:
.
Как видно данное выражение зависит от сопротивления нагрузки и как и в случае линейных электрических цепей без магнитных связей данное сопротивление можно выбрать таким образом, чтобы добиться наибольшего возможного значения коэффициента передачи мощности. Определим оптимальное значение сопротивления нагрузки. Для этого исследуем полученную функцию на экстремум:
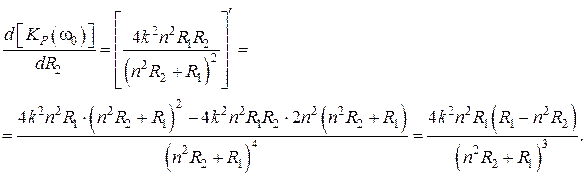
Тогда:
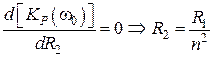, (8.29)
а выражения для центральной частоты и максимального коэффициента передачи мощности принимают вид:
, 
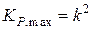. (8.30)
Преобразуем выражение (8.27) с учетом полученных выражений (8.29) и (8.30):
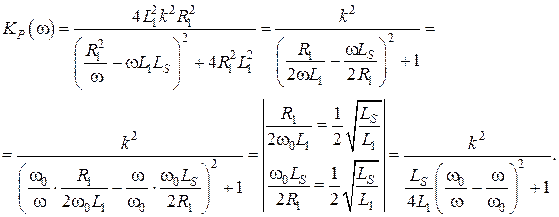
Таким образом, коэффициент передачи мощности согласующего трансформатора имеет вид:
(8.31)
Вид данной зависимости в логарифмическом масштабе представлен на рис. 8.12.
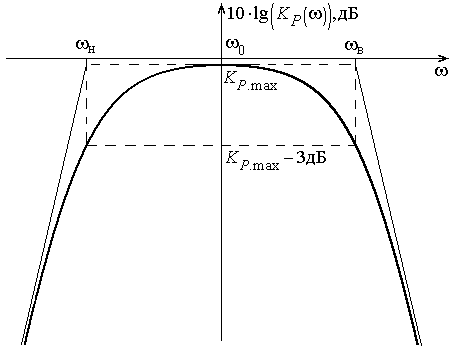
Рис. 8.12 – Частотная зависимость коэффициента передачи мощности согласующего трансформатора в логарифмическом масштабе
Из рис. 8.12 видно, что трансформатор выполняет свою функцию передачи мощности от генератора к нагрузке в пределах полосы частот от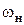 
до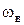 
, когда коэффициент мощность уменьшается относительно максимального значения не более чем на 3 дБ. Определим значения данных частот:
,
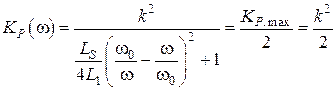тогда
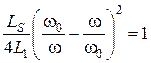. (8.32)
Уравнение (8.32) определяет значение верхней и нижней граничных частот среза. Для практики важен случай, когда выполняются следующие соотношения между граничными частотами среза и центральной частотой:
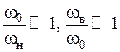. (8.33)
Трансформатор, для которого условия (8.33) выполняются называется широкополосным.
Тогда для верхнее и нижней граничных частот среза выражение (8.32) принимает вид:
или же
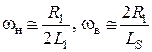. (8.34)
Из полученных выражений видно, что улучшить частотные свойства трансформатора, т.е. расширить рабочий частотный диапазон можно увеличивая 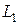и уменьшая 
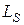, то есть, приближая по свойствам трансформатор к идеальному.
Из рис. 8.12 видно, что за пределами полосы пропускания спад коэффициента передачи мощности в логарифмическом масштабе происходит практически линейно и график стремится к своим асимптотам. Определим эти асимптоты:
· для частот ниже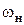
;
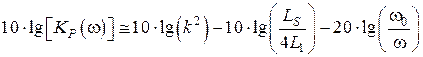· для частот выше
.
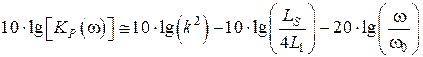Таким образом, за пределами полосы пропускания график коэффициента передачи мощности имеет наклон 20 дБ на декаду.
|
|
|
