 |
Показательная форма комплексного числа.
|
|
|
|
ОДОБРЕНО
Цикловой методической комиссией
общеобразовательных и естественнонаучных
дисциплин:
Протокол № ___
от «____» _________________ 2016 г.
Председатель ЦМК:
_____________ Криницына Н.А.
«МАТЕМАТИКА»
Методические рекомендации для студентов
решения задач по математики.
для специальностей:
26.02.06 «Эксплуатация судового электрооборудования и средств автоматики»
23.02.03 «Техническое обслуживание и ремонт автомобильного транспорта»
23.02.01 «Организация перевозок и управление на транспорте (по видам)»
26.02.05 «Эксплуатация судовых энергетических установок»
26.02.03 «Судовождение»
Преподаватель:
Абраменкова В.П..
Пермь
Образцы решения некоторых заданий контрольных работ
Комплексные числа.
Пример 1. Построим на комплексной плоскости следующие комплексные числа:
 ,
,  ,
, 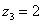
 ,
,  ,
, 
 ,
,  ,
,  ,
, 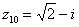

Числа  ,
, 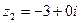 ,
,  – комплексные числа с нулевой мнимой частью.
– комплексные числа с нулевой мнимой частью.
Числа  ,
,  ,
,  , – это, наоборот, чисто мнимые числа, т.е. числа с нулевой действительной частью. Они располагаются строго на мнимой оси
, – это, наоборот, чисто мнимые числа, т.е. числа с нулевой действительной частью. Они располагаются строго на мнимой оси  .
.
В числах 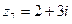 ,
,  ,
,  ,
,  и действительная и мнимая части не равны нулю. Такие числа тоже обозначаются точками на комплексной плоскости, при этом, к ним принято проводить радиус-векторы из начала координат (обозначены красным цветом на чертеже). Радиус-векторы к числам, которые располагаются на осях, обычно не чертят, потому, что они сливаются с осями.
и действительная и мнимая части не равны нулю. Такие числа тоже обозначаются точками на комплексной плоскости, при этом, к ним принято проводить радиус-векторы из начала координат (обозначены красным цветом на чертеже). Радиус-векторы к числам, которые располагаются на осях, обычно не чертят, потому, что они сливаются с осями.
Сложение комплексных чисел.
Пример 2. 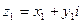 и
и 
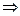

Сложить два комплексных числа 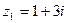 ,
, 
Для того чтобы сложить два комплексных числа нужно сложить их действительные и мнимые части:

Пример 3. Вычитание комплексных чисел. 
Найти разности комплексных чисел: 

Умножение комплексных чисел.
|
|
|
 ·
· 
Пример 4. Найти произведение комплексных чисел  ,
, 
Необходимо раскрыть скобки по правилу умножения многочленов, главное, помнить, что  .
.

Понятно, что 
Пример 5. Деление комплексных чисел.
Даны комплексные числа  ,
,  . Найти частное.
. Найти частное.

Пример 6.1. Представить в тригонометрической форме число  . Найдем его модуль и аргумент.
. Найдем его модуль и аргумент.  .
.
Очевидно, что  (число лежит непосредственно на действительной положительной полуоси). Таким образом, число в тригонометрической форме:
(число лежит непосредственно на действительной положительной полуоси). Таким образом, число в тригонометрической форме:  .
.
Обратное проверочное действие: 
Пример 6.2. Представить в тригонометрической форме число  . Найдем его модуль и аргумент.
. Найдем его модуль и аргумент. 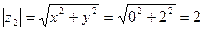 .
. 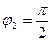
Таким образом, число в тригонометрической форме:  .
.
Используя таблицу значений тригонометрических функций, легко обратно получить алгебраическую форму числа (заодно выполнив проверку):

Пример 6.3. Представить в тригонометрической форме число  . Найдем его модуль и аргумент.
. Найдем его модуль и аргумент. 
Очевидно, что  (или 180 градусов). Таким образом, число в тригонометрической форме:
(или 180 градусов). Таким образом, число в тригонометрической форме:  .
.
Проверка: 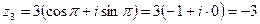
Пример 6.4. Представить в тригонометрической форме число  .
.
Найдем его модуль и аргумент.  ,
,
 (-90 градусов), и, соответственно:
(-90 градусов), и, соответственно:  .
.
Рассмотрим более распространенные случаи.
Модуль вычисляется по формуле  . А вот формулы для нахождения аргумента будут разными, это зависит от того, в какой координатной четверти лежит число
. А вот формулы для нахождения аргумента будут разными, это зависит от того, в какой координатной четверти лежит число 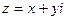 . При этом возможны три варианта:
. При этом возможны три варианта:
1) Если 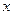 > 0 (1-я и 4-я координатные четверти, или правая полуплоскость), то аргумент нужно находить по формуле
> 0 (1-я и 4-я координатные четверти, или правая полуплоскость), то аргумент нужно находить по формуле 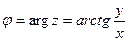 .
.
2) Если x < 0, y > 0 (2-я координатная четверть), то аргумент нужно находить по формуле  .
.
3) Если x < 0, y < 0 (3-я координатная четверть), то аргумент нужно находить по формуле  .
.
Пример 6.5. Представим в тригонометрической форме число  . Найдем его модуль и аргумент.
. Найдем его модуль и аргумент.  ,
,  , x >0, y > 0
, x >0, y > 0  .
.  ,
, 
Следовательно 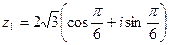
Пример 6.6. Представим в тригонометрической форме число  . Найдем его модуль и аргумент.
. Найдем его модуль и аргумент.  ,
,  x < 0, y > 0
x < 0, y > 0  .
.


Следовательно 
Пример 6.7. Представим в тригонометрической форме число  . Найдем его модуль и аргумент.
. Найдем его модуль и аргумент.  ,
,  , x <0, y < 0
, x <0, y < 0  .
.  ,
, 
|
|
|
Следовательно 
Пример 6.8. Представим в тригонометрической форме число  . Найдем его модуль и аргумент.
. Найдем его модуль и аргумент.  ,
, 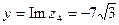 , x >0, y < 0
, x >0, y < 0  .
.  ,
, 
Следовательно 
Показательная форма комплексного числа.
Любое комплексное число 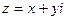 (кроме нуля) можно записать в показательной форме:
(кроме нуля) можно записать в показательной форме:  , где
, где  – это модуль комплексного числа, а
– это модуль комплексного числа, а  – аргумент комплексного числа.
– аргумент комплексного числа.
Пример 7.1. Представить в показательной форме комплексные числа:  ,
,  ,
,  ,
,  .
.
9.1.  ,
,  ,
, 
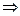
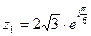
9.2.  ,
,  ,
, 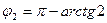
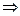
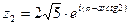
9.3.  ,
,  ,
, 
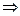

9.4.  ,
,  ,
, 
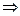

Пример1.. Решить систему линейных уравнений, используя правило Крамера и метод обратной матрицы:

Решение.
1. Правило Крамера.
Находим определитель системы:

Следовательно, система является определённой. Для нахождения её решения вычисляем определители:



По формулам Крамера находим:


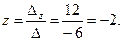
Ответ: 
Пример 2. Решить уравнение:  .
.
Решение. Данное уравнение относится к классу дифференциальных уравнений первого порядка с разделяющимися переменными. Разделим переменные:
 . Теперь уравнение можно интегрировать:
. Теперь уравнение можно интегрировать:  . Находим неопределенные интегралы:
. Находим неопределенные интегралы:  , откуда:
, откуда:  - это общий интеграл данного дифференциального уравнения. Ответ:
- это общий интеграл данного дифференциального уравнения. Ответ: 
Пример 3. Решить уравнение  при условии
при условии  .
.
Решение. Данное уравнение является линейным дифференциальным уравнением первого порядка, для его решения применяем метод Бернулли. Делаем замену:  , где
, где 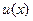 и
и  - неизвестные функции. Получаем:
- неизвестные функции. Получаем:  или
или  . Неизвестную функцию
. Неизвестную функцию  найдем из условия
найдем из условия  :
:  ,
,  , откуда
, откуда  . Тогда для нахождения второй неизвестной функции
. Тогда для нахождения второй неизвестной функции 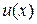 нужно решить уравнение:
нужно решить уравнение:  , откуда:
, откуда:  . Тогда
. Тогда  и путем интегрирования последнего равенства получаем
и путем интегрирования последнего равенства получаем  . Тогда общее решение исходного уравнения имеет вид:
. Тогда общее решение исходного уравнения имеет вид:  . Для нахождения частного решения воспользуемся начальным условием:
. Для нахождения частного решения воспользуемся начальным условием:  . Подставляя соответствующие значения переменных
. Подставляя соответствующие значения переменных 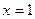 и
и  в общее решение, получаем:
в общее решение, получаем:  , откуда
, откуда  . Тогда частное решение данной задачи имеет вид:
. Тогда частное решение данной задачи имеет вид:  . Ответ:
. Ответ:  .
.
Пример 4. Решить уравнение: у ² +2 у' +5 у = 0.
Решение. Данное уравнение является линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами. Для его решения составляем характеристическое уравнение: 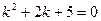 . Это алгебраическое уравнение второго порядка, его корни – комплексные, сопряженные числа:
. Это алгебраическое уравнение второго порядка, его корни – комплексные, сопряженные числа:  . Тогда общее решение данного уравнения имеет вид:
. Тогда общее решение данного уравнения имеет вид:  . Ответ:
. Ответ:  .
.
|
|
|
Пример 5. Исследовать на сходимость ряд 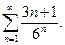
Решение. Для исследования данного ряда на сходимость можно применить признак Даламбера. Для этого находим  и
и  . Тогда:
. Тогда: 

 , следовательно, по признаку Даламбера данный числовой ряд сходится.
, следовательно, по признаку Даламбера данный числовой ряд сходится.
Пример 7. Бросают три игральные кости. Найти вероятность того, что на верхних гранях появится число очков, сумма которых делится на пять.
Решение. Определим испытание и его результат, т. е. элементарное событие. Испытанием является бросание трех игральных костей; результатом – одно из сочетаний очков 1,..., 6 на верхних гранях трех костей.
Исследуемое событие А – сумма очков на трех костях делится на пять. Вероятность события А вычислим с помощью формулы:
Р(А) = m/n.
Общее количество элементарных событий п можно найти по правилу умножения. На каждой игральной кости 6 граней и все они могут сочетаться со всеми гранями других костей. Итак, получаем n = 6 × 6 × 6 = 216.
Количество элементарных событий т, входящих в состав события А или благоприятствующих событию А,найдем выписав всевозможные результаты испытаний и оставив из них только те, для которых сумма очков на всех трех костях делится на пять. Можно облегчить работу, выписав всевозможные исходы бросания первых двух костей, сочетая с ними подходящие значения количества очков, выпавших на третьей кости. Имеем:
В результате получаем, что Р (т) = 43, значит, Р (А) = 43/216.
Ответ: Р (А) = 43/216.
Пример 8. Вероятность выигрыша по одному билету равна 0,2. Имеется шесть билетов. Найти вероятности следующих событий: а) два билета будут выигрышными; б) выигрышных билетов будет от двух до четырех.
Решение. Для вычисления искомых вероятностей воспользуемся формулой Бернулли:  . По условию задачи
. По условию задачи  ,
, 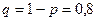 .
.
|
|
|
а) Рассмотрим случайное событие А: два билета из шести будут выигрышными. Его вероятность:  .
.
б) Рассмотрим случайное событие В: выигрышных билетов будет от двух до четырех. Это сложное событие состоит из следующих:
В1: два билета из шести будут выигрышными;
В2: три билета из шести будут выигрышными;
В3: четыре билета из шести будут выигрышными.
Тогда В= В1+В2+В3 и Р(В) = Р(В1)+Р(В2)+Р(В3).
Находим по формуле Бернулли соответствующие вероятности:
 ,
,
 ,
,
 .
.
Тогда искомая вероятность: Р(В) = 0,2458+0,0492+0,0061=0,3011
Ответ: P(B)=0,3011.
Пример 9. После обработки результатов эксперимента составлена таблица, в первой строке которой указаны группы возможных значений некоторой случайной величины хi, а во второй строке – численность каждой группы значений m:
| х i | 21 | 17 | 35 | 11 |
| m i | 3 | 11 | 14 | 5 |
Найти объем выборки 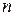 ; относительные частоты
; относительные частоты  , соответствующие каждой отдельной группе значений случайной величины; составить вариационный ряд распределения данной случайной величины. Найти числовые характеристики выборки: среднее арифметическое, выборочную дисперсию и среднеквадратическое отклонение.
, соответствующие каждой отдельной группе значений случайной величины; составить вариационный ряд распределения данной случайной величины. Найти числовые характеристики выборки: среднее арифметическое, выборочную дисперсию и среднеквадратическое отклонение.
Решение. Найдем объем выборки n по формуле:  , где
, где  – число столбцов в таблице. Тогда n = 3+11+14+5=33.
– число столбцов в таблице. Тогда n = 3+11+14+5=33.
Относительные частоты  , соответствующие каждой отдельной группе значений случайной величины, находим по формулам:
, соответствующие каждой отдельной группе значений случайной величины, находим по формулам:  . Получаем:
. Получаем:  ,
,  ,
,  ,
, 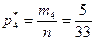 .
.
Составим вариационный ряд распределения данной случайной величины:
| х i | ||||

| 1/11 | 1/3 | 14/33 | 5/33 |
Находим числовые характеристики выборки:
а) среднее арифметическое находим по формуле:
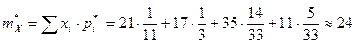
б) выборочная дисперсия находится по формуле:  .
.
Получаем: 
в) среднеквадратическое отклонение:  .
.
|
|
|


