| №п/п
| Задания
| Ответы
|
| Раздел: ИНТЕГРАЛЫ ФОП.
|
Тема 8.1. Непосредственное интегрирование:Первообразная функция, её свойства и нахождение. Вычисление неопределённых интегралов непосредственным интегрированием. Вычисление интегралов  , где , где  - табличный интеграл. - табличный интеграл.
|
| 1.
| Множество первообразных функции  имеет вид:
1) имеет вид:
1)  2) 2) 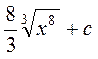 3) 3) 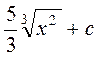 4) 4) 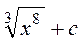
| 1)
|
| 2.
| Функция  является первообразной для функции:
1) является первообразной для функции:
1)  2) 2)  3) 3) 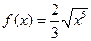 4) 4) 
| 1)
|
| 3.
| Интеграл  равен:
1) равен:
1)  2) 2)  3) 3)  4)
4) 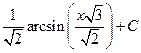
| 1)
|
| 4.
| Интеграл  равен:
1) равен:
1)  2) 2)  3) 3)  4) 4) 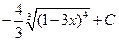
| 1)
|
| 5.
| Интеграл  равен:
1) равен:
1)  2) 2)  3) 3)  4) 4) 
| 1)
|
| 6.
| Функция  является первообразной для функции является первообразной для функции  , если , если  , ,  ( ( - целые числа).
Ответ записать в виде: - целые числа).
Ответ записать в виде:  . .
| 3,-3
|
| 7.
| Интеграл  равен:
1) равен:
1) 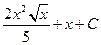 1) 1)  1) 1)  1) 1) 
| 1)
|
Тема 8.2 Интегрирование-1:Непосредственное интегрирование, заменой переменной, по частям неопределённых интегралов, в том числе вычисление интегралов вида  , ,  , ,  , ,  , ,  , ,  , ,  . .
|
| 1.
| Неопределённый интеграл  равен равен  , где , где  , ,  ( ( - целые числа). Ответ представить в виде: - целые числа). Ответ представить в виде: 
| 4,7
|
| 2.
| Неопределённый интеграл  равен равен 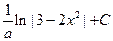 , где , где  ( ( - целое число). Ответ представить в виде: - целое число). Ответ представить в виде: 
| -4
|
| 3.
| Неопределённый интеграл  равен равен  , где , где  , ,  ( ( - целые положительные числа). Ответ представить в виде: - целые положительные числа). Ответ представить в виде: 
| 12,11
|
| 4.
| Неопределённый интеграл  равен равен  , где , где  , ( , ( - целое число). Ответ представить в виде: - целое число). Ответ представить в виде: 
|
|
| 5.
| Неопределённый интеграл  равен равен  , где , где  , ,  ( ( - целые числа). Ответ представить в виде: - целые числа). Ответ представить в виде: 
| -2,-4
|
| 6.
| Неопределённый интеграл  равен равен  , где , где  , ( , ( - целое число). Ответ представить в виде: - целое число). Ответ представить в виде: 
|
|
| 7.
| Неопределённый интеграл  равен равен  , где , где  , ,  ( ( - целые числа). Ответ представить в виде: - целые числа). Ответ представить в виде: 
| 3,9
|
|
| Неопределённый интеграл имеет вид  , тогда , тогда  , где , где  , ( , ( - целое число). Ответ представить в виде: - целое число). Ответ представить в виде: 
|
|
Тема 8.3 Интегрирование-2:Непосредственное интегрирование, заменой переменной, по частям неопределённых интегралов. Нахождение интегралов  , ,  , ,  . .
|
| 1.
| Интеграл  равен равен  , где , где  , ,  ( ( - целые числа). Ответ представить в виде: - целые числа). Ответ представить в виде: 
| 2,7
|
Тема 8.4: Интегрирование-3:Интегрирование рациональных дробей. Нахождение интегралов  , ,  , ,  , ,  . Интегрирование заменой переменной и по частям. Несобственные интегралы первого рода (их сходимость и расходимость). . Интегрирование заменой переменной и по частям. Несобственные интегралы первого рода (их сходимость и расходимость).
|
| 1.
| Интеграл  равен равен  , где , где  , ,  ( ( - целые числа).
Ответ представить в виде: - целые числа).
Ответ представить в виде: 
| 2,8
|
| 2.
| Из несобственных интегралов А: 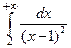 В: В:  расходятся:
1) только А 2) только В 3) оба сходятся 4) оба расходятся расходятся:
1) только А 2) только В 3) оба сходятся 4) оба расходятся
| 2)
|
| 3.
| Неопределённый интеграл  равен равен  ,
где ,
где  , ,  ( ( - целые числа). Ответ представить в виде: - целые числа). Ответ представить в виде: 
| 4,-1
|
| Тема 8.5: Приложения интеграла-1:Площадь плоской фигуры в декартовых координатах.
|
| 1.
| Площадь фигуры, ограниченной линиями  , равна:
1) , равна:
1)  2) 2)  3) 3)  4) 4)  5) 5) 
| 1)
|
| 2.
| Площадь фигуры, ограниченной линиями  , равна…
Записать ответ. , равна…
Записать ответ.
|
|
| Тема 8.6: Приложения интеграла-2:площадь фигуры, объём тела вращения, длина дуги кривой, среднее значение непрерывной на отрезке функции.
|
| 1.
| Длина дуги кривой  на отрезке на отрезке  равна равна  , где , где  , ,  ( ( - целые числа). Ответ представить в виде: - целые числа). Ответ представить в виде: 
| 3,2
|
| 2.
| Объём тела, полученного при вращении вокруг оси  плоской фигуры, ограниченной линиями плоской фигуры, ограниченной линиями 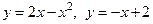 , равен , равен  , где , где  ( ( - целое число). Ответ представить в виде: - целое число). Ответ представить в виде: 
|
|
| 3.
| Среднее значение  функции функции  на отрезке на отрезке  равно равно  , где , где  , ,  ( ( - целые числа). Ответ представить в виде: - целые числа). Ответ представить в виде: 
| 1,-1
|
| Тема 8.7: Двойной интеграл-1.Повторный и двойной интеграл, их вычисление в декартовых координатах.
|
| 1.
| Повторный интеграл  равен… Записать ответ. равен… Записать ответ.
|
|
| 2.
| Двойной интеграл 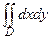 по области по области  равен равен  , где , где  , ,  ( ( - целые числа). Ответ представить в виде несократимой дроби: - целые числа). Ответ представить в виде несократимой дроби: 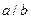
| 8/3
|
| Тема 8.8: Двойной интеграл-2.Повторный и двойной интеграл, их вычисление в декартовых координатах.
|
| 1.
| Двойной интеграл  по области по области  , ограниченной линиями , ограниченной линиями  , равен , равен  , где , где  , ,  ( ( - целые числа).
Ответ представить в виде: - целые числа).
Ответ представить в виде: 
| 5,-3
|
| 2.
| Двойной интеграл 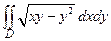 по области по области  , ограниченной линиями , ограниченной линиями  равен равен  , где , где  ( ( - целое число).
Ответ представить в виде: - целое число).
Ответ представить в виде: 
|
|
Тема 8.11: Определённый интеграл -1.Непосредственное интегрирование, заменой переменной, по частям, в том числе вычисление интегралов вида  , ,  , ,  , ,  , ,   , ,  , ,  , ,  . Формула Ньютона-Лейбница. Несобственные интегралы первого рода (сходимость и расходимость). . Формула Ньютона-Лейбница. Несобственные интегралы первого рода (сходимость и расходимость).
|
| 1.
| Определённый интеграл  равен равен  , где , где  , ,  ( ( - целые числа). Ответ представить в виде: - целые числа). Ответ представить в виде: 
| 3,2
|
| 2.
| Несобственный интеграл  равен:
1) равен:
1)  2) 2)  3) 3) 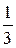 4) 4)  5) 5) 
| 3)
|
| Раздел: РЯДЫ.
|
| Тема 9.1: Числовые ряды-1.Задание числового ряда. Исследование на сходимость и расходимость числовых рядов с помощью достаточного признака расходимости ряда, признаков сходимости знакоположительных числовых рядов (предельного признака сравнения, признака Даламбера, радикального признака Коши).
|
| 1.
| Известны первые три члена числового ряда:  . Тогда формула общего члена этого ряда имеет вид:
1) . Тогда формула общего члена этого ряда имеет вид:
1)  2) 2) 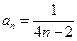 3) 3)  4) 4) 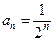
| 3)
|
| 2.
| Применив радикальный признак Коши  к ряду к ряду  , получаем:
1) , получаем:
1)  2) 2)  3) 3) 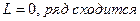 4)
4)  5) 5) 
| 1)
|
| 3.
| Ряд  сходится по признаку сравнения с рядом сходится по признаку сравнения с рядом  при:
1) при:
1)  2) 2)  3) 3)  4) 4)  5) 5) 
| 4)
|
| 4.
| Ряд  расходится по радикальному признаку Коши, так как расходится по радикальному признаку Коши, так как  , где , где  1)
1)  2) 2) 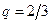 3) 3)  4) 4)  5) 5) 
| 1)
|
| 5.
| Ряд  сходится по признаку Даламбера, так как сходится по признаку Даламбера, так как  , где , где  1)
1)  2) 2)  3) 3)  4) 4)  5) 5) 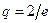
| 1)
|
| Тема 9.2: Числовые ряды-2.Исследование на сходимость и расходимость числовых рядов с помощью достаточного признака расходимости ряда, признаков сходимости знакоположительных числовых рядов (предельного признака сравнения, признака Даламбера, радикального признака Коши), признака Лейбница сходимости знакочередующегося ряда. Исследование числовых рядов на абсолютную и условную сходимость.
|
| 1.
| Ряд 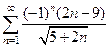 :
1)расходится2)сходится условно 3)сходится абсолютно 4)сходится :
1)расходится2)сходится условно 3)сходится абсолютно 4)сходится
| 1)
|
| 2.
| Из рядов А:  В: В:  cходятся:
1)толькоA 2)только B 3)оба ряда сходятся4)ни один не сходится cходятся:
1)толькоA 2)только B 3)оба ряда сходятся4)ни один не сходится
| 2)
|
| 3.
| Для знакочередующихся рядов А:  В: В:  справедливо одно из следующих утверждений:
1) Aсходится абсолютно, Всходится условно
2) Aсходится абсолютно, Всходится абсолютно
3) Aсходится абсолютно, Врасходится
4) Aсходится условно, Всходится условно
5) Aрасходится, Всходится условно
справедливо одно из следующих утверждений:
1) Aсходится абсолютно, Всходится условно
2) Aсходится абсолютно, Всходится абсолютно
3) Aсходится абсолютно, Врасходится
4) Aсходится условно, Всходится условно
5) Aрасходится, Всходится условно
| 1)
|
|
| Установите соответствие между видами сходимости и знакопеременными рядами.
1: Абсолютно сходится 1:  2: Условно сходится 2:
2: Условно сходится 2:  3: Расходится 3:
3: Расходится 3: 
| 1-1
2-3
3-2
|
Тема 9.3: Степенные ряды-1:Нахождение радиуса и интервала сходимости степенного ряда. Нахождение коэффициентов  разложения функции в ряды Тейлора и Маклорена. разложения функции в ряды Тейлора и Маклорена.
|
|
| Радиус сходимости степенного ряда  равен равен  . Тогда интервал сходимости этого ряда имеет вид:
1) . Тогда интервал сходимости этого ряда имеет вид:
1)  2) 2) 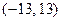 3) 3)  4) 4) 
| 4)
|
| 2.
| Радиус 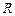 сходимости степенного ряда сходимости степенного ряда  равен…: Записать ответ. равен…: Записать ответ.
| 4/5
|
| 3.
| Интервалом сходимости степенного ряда  является интервал:
1) является интервал:
1)  2) 2)  3) 3)  4) 4) 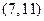 5) 5) 
| 1)
|
| 4.
| Если  , то коэффициент , то коэффициент  разложения данной функции в ряд Тейлора по степеням разложения данной функции в ряд Тейлора по степеням  равен…: Записать ответ. равен…: Записать ответ.
|
|
Тема 9.4: Степенные ряды-2:Радиус сходимости, интервал сходимости, область сходимости степенного ряда. Нахождение первых членов разложения функций в ряды Тейлора и Маклорена. Нахождение коэффициентов  разложения функции в ряды Тейлора и Маклорена. разложения функции в ряды Тейлора и Маклорена.
|
| 1.
| При разложении функции 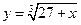 в ряд Маклорена первые три отличные от нуля члена ряда имеют вид
1) в ряд Маклорена первые три отличные от нуля члена ряда имеют вид
1)  2) 2) 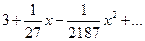 3) 3)  4)
4)  5) 5) 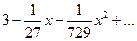
| 2)
|
| 2.
| Количество целых чисел принадлежащих интервалу сходимости степенного ряда  равно… Записать ответ. равно… Записать ответ.
|
|
| 3.
| Если  то коэффициент то коэффициент  разложения данной функции в ряд Тейлора по степеням разложения данной функции в ряд Тейлора по степеням 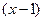 равен…: Записать ответ. равен…: Записать ответ.
| -13/72
|
| 4.
| Соответствие степенного ряда его радиусу сходимости:
1:  1: 1:  2:
2: 2: 2:  3:
3:  3: 3:  В ответе указать пары, соответствующих друг другу степенных рядов и их радиусов сходимости.
В ответе указать пары, соответствующих друг другу степенных рядов и их радиусов сходимости.
| 1-1
2-2
3-3
|
| 5.
| Областью сходимости степенного ряда  является промежуток:
1) является промежуток:
1)  2) 2)  3) 3)  4) 4)  5) 5) 
| 2)
|
| Тема 9.5: Ряды_теория-1:Определения знакоположительного и знакочередующегося числовых рядов, степенного ряда. Определения рядов Тейлора и Маклорена. Формулировка необходимого признака сходимости и достаточного признака расходимости числового ряда. Условия сходимости и расходимости по признаку Даламбера и радикальному признаку Коши.
|
| 1.
| Соответствие ряда его названию:
1:  1: знакоположительный
2: 1: знакоположительный
2:  2: знакочередующийся
3: 2: знакочередующийся
3:  3: степенной
В ответе указать пары, соответствующих друг другу рядов и их названий. 3: степенной
В ответе указать пары, соответствующих друг другу рядов и их названий.
| 1-3
2-2
3-1
|
| Раздел: ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ.
|
Тема 10.1: ДУ первого порядка-1.Простейшее ДУ:  . Дифференциальное уравнение с разделяющимися переменными, линейное ДУ,нахождение их общих и частных решений. . Дифференциальное уравнение с разделяющимися переменными, линейное ДУ,нахождение их общих и частных решений.
|
|
| Общий интеграл дифференциального уравнения  имеет вид:
1) имеет вид:
1)  2) 2)  3) 3) 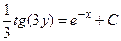 4) 4)  5) 5) 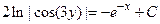
| 4)
|
| 2.
| Дано дифференциальное уравнение  . Тогда функция . Тогда функция  является его решением при является его решением при  равном:
1) равном:
1)  2) 2)  3) 3)  4) 4)  5) 5) 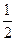
| 1)
|
| 3.
| Общий интеграл дифференциального уравнения  имеет вид:
1) имеет вид:
1)  2) 2)  3) 3)  4)
4)  5) 5) 
| 4)
|
| 4.
| Общее решение дифференциального уравнения  имеет вид:
1) имеет вид:
1)  2) 2)  3) 3)  4) 4) 
| 1)
|
| 5.
| Частное решение дифференциального уравнения  при при  имеет вид:
1) имеет вид:
1) 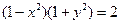 2) 2)  3) 3)  4) 4) 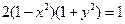
| 1)
|
| 6.
| Из перечисленных ниже функций общим решением дифференциального уравнения  является:
1) является:
1)  2) 2)  3) 3)  4) 4)  5) 5) 
| 1)
|
| Тема 10.2: ДУ первого порядка-2. Дифференциальное уравнение с разделяющимися переменными, линейное ДУ,нахождение их общих и частных решений.
|
| 1.
| Дана задача Коши:  , ,  . Тогда значение . Тогда значение  её решения её решения  равно… Записать ответ. равно… Записать ответ.
|
|
Тема 10.3: ДУ высших порядков-1.Общее решение простейшего ДУ  . Общее и частные решения линейного однородного ДУ второго порядка с постоянными коэффициентами . Общее и частные решения линейного однородного ДУ второго порядка с постоянными коэффициентами  . Соответствие ОЛДУ второго порядка корням его характеристического уравнения. . Соответствие ОЛДУ второго порядка корням его характеристического уравнения.
|
| 1.
| Общим решением дифференциального уравнения  является функция:
1) является функция:
1) 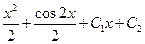 2) 2) 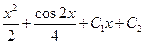 3) 3) 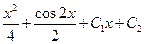 4)
4)  5) 5) 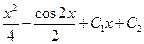
| 4)
|
| 2.
| Общее решение дифференциального уравнения  имеет вид:
1) имеет вид:
1)  2) 2)  3) 3)  4)
4)  5) 5) 
| 4)
|
| 3.
| Частное решение дифференциального уравнения  при начальных условиях: при начальных условиях:  имеет вид:
1) имеет вид:
1)  2) 2)  3) 3) 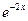 4) 4)  5) 5) 
| 3)
|
| 4.
| Соответствие дифференциального уравнения корням его характеристического уравнения:
1:  1: 1:  2:
2: 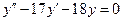 2: 2: 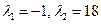 3:
3:  3: 3:  В ответе указать пары, соответствующих друг другу ДУ и корней их характеристических уравнений.
В ответе указать пары, соответствующих друг другу ДУ и корней их характеристических уравнений.
| 1-1
2-2
3-3
|
Тема 10.4: ДУ высших порядков-2.Простейшее ДУ ( ), ДУ допускающие понижение порядка ( ), ДУ допускающие понижение порядка (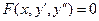 , ,  , ,  ), линейные однородные и неоднородные ДУ с постоянными коэффициентами и правой частью специального вида, нахождение их общих и частных решений. ), линейные однородные и неоднородные ДУ с постоянными коэффициентами и правой частью специального вида, нахождение их общих и частных решений.
|
| 1.
| Дана задача Коши:  . Тогда значение . Тогда значение  её решения её решения  равно… Записать ответ. равно… Записать ответ.
|
|
| 2.
| Соответствие дифференциального уравнения его общему решению:
1:  1: 1:  2:
2:  2: 2:  3:
3:  3: 3:  В ответе указать пары, соответствующих друг другу ДУ и их общих решений.
В ответе указать пары, соответствующих друг другу ДУ и их общих решений.
| 1-1
2-2
3-3
|
| 3.
| Частное решение  неоднородного линейного дифференциального уравнения неоднородного линейного дифференциального уравнения  имеет вид имеет вид 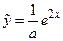 ,где ,где  ( ( - целое число).
Ответ записать в виде: - целое число).
Ответ записать в виде: 
|
|
| 4.
| Общее решение дифференциального уравнения  имеет вид:
1) имеет вид:
1)  2) 2)  3) 3)  4)
4)  5) 5) 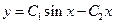
| 3)
|
| 5.
| Общее решение дифференциального уравнения  имеет вид имеет вид  , где , где  ( ( - целое число). Ответ записать в виде: - целое число). Ответ записать в виде: 
| -2
|
| 6.
| Частное решение  неоднородного линейного ДУ: неоднородного линейного ДУ:  имеет вид имеет вид  , где , где   ( ( - целые числа).
Ответ записать в виде: - целые числа).
Ответ записать в виде: 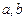
| 4,23
|
| 7.
| Частное решение  неоднородного линейного дифференциального уравнения неоднородного линейного дифференциального уравнения 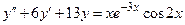 представимо в виде:
1) представимо в виде:
1)  2) 2)  3)
3)  4) 4)  5)
5) 
| 5)
|
| 8.
| Общим решением дифференциального уравнения  является функция:
1) является функция:
1)  2) 2)  3) 3)  4) 4)  5) 5) 
| 1)
|
Тема 10.5: ДУ (теория-1):Определение порядка дифференциального уравнения. Определение типа дифференциального уравнения первого порядка (ДУ с разделяющимися переменными; однородное; линейное; Бернулли). Определение типа дифференциального уравнения высшего порядка (простейшее ( ); допускающее понижение порядка ( ); допускающее понижение порядка (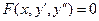 , ,  ); линейное однородное и неоднородное ДУ порядка ); линейное однородное и неоднородное ДУ порядка  ). ).
|
| 1.
| Соответствие дифференциального уравнения его названию:
1:  1: линейное
2: 1: линейное
2: 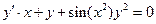 2: Бернулли
3: 2: Бернулли
3:  3: однородное
4: 3: однородное
4:  4: с разделяющимися переменными
В ответе указать пары, соответствующих друг другу ДУ и их названий. 4: с разделяющимися переменными
В ответе указать пары, соответствующих друг другу ДУ и их названий.
| 1-1
2-2
3-3
4-4
|
| 2.
| Порядок дифференциального уравнения  равен…
Записать ответ. равен…
Записать ответ.
|
|
| 3.
| Из ниже перечисленных дифференциальных уравнений высшего порядка понижение порядка допускают уравнения:
1)  2) 2)  3) 3)  4)
4) 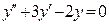 5) 5)  Указать все правильные ответы.
Указать все правильные ответы.
| 1)2)4)
|

 , где
, где  - табличный интеграл.
- табличный интеграл.
 имеет вид:
1)
имеет вид:
1)  2)
2) 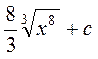 3)
3) 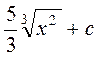 4)
4) 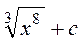
 является первообразной для функции:
1)
является первообразной для функции:
1)  2)
2)  3)
3) 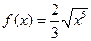 4)
4) 
 равен:
1)
равен:
1)  2)
2)  3)
3)  4)
4) 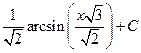
 равен:
1)
равен:
1)  2)
2)  3)
3)  4)
4) 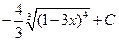
 равен:
1)
равен:
1)  2)
2)  3)
3)  4)
4) 
 является первообразной для функции
является первообразной для функции  , если
, если  ,
,  (
( - целые числа).
Ответ записать в виде:
- целые числа).
Ответ записать в виде:  .
.
 равен:
1)
равен:
1) 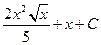 1)
1)  1)
1)  1)
1) 
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
.
 равен
равен  , где
, где  ,
,  (
( - целые числа). Ответ представить в виде:
- целые числа). Ответ представить в виде: 
 равен
равен 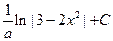 , где
, где  (
( - целое число). Ответ представить в виде:
- целое число). Ответ представить в виде: 
 равен
равен  , где
, где  ,
,  (
( - целые положительные числа). Ответ представить в виде:
- целые положительные числа). Ответ представить в виде: 
 равен
равен  , где
, где  , (
, ( - целое число). Ответ представить в виде:
- целое число). Ответ представить в виде: 
 равен
равен  , где
, где  ,
,  (
( - целые числа). Ответ представить в виде:
- целые числа). Ответ представить в виде: 
 равен
равен  , где
, где  , (
, ( - целое число). Ответ представить в виде:
- целое число). Ответ представить в виде: 
 равен
равен  , где
, где  ,
,  (
( - целые числа). Ответ представить в виде:
- целые числа). Ответ представить в виде: 
 , тогда
, тогда  , где
, где  , (
, ( - целое число). Ответ представить в виде:
- целое число). Ответ представить в виде: 
 ,
,  ,
,  .
.
 равен
равен  , где
, где  ,
,  (
( - целые числа). Ответ представить в виде:
- целые числа). Ответ представить в виде: 
 ,
,  ,
,  ,
,  . Интегрирование заменой переменной и по частям. Несобственные интегралы первого рода (их сходимость и расходимость).
. Интегрирование заменой переменной и по частям. Несобственные интегралы первого рода (их сходимость и расходимость).
 равен
равен  , где
, где  ,
,  (
( - целые числа).
Ответ представить в виде:
- целые числа).
Ответ представить в виде: 
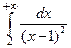 В:
В:  расходятся:
1) только А 2) только В 3) оба сходятся 4) оба расходятся
расходятся:
1) только А 2) только В 3) оба сходятся 4) оба расходятся
 равен
равен  ,
где
,
где  ,
,  (
( - целые числа). Ответ представить в виде:
- целые числа). Ответ представить в виде: 
 , равна:
1)
, равна:
1)  2)
2)  3)
3)  4)
4)  5)
5) 
 , равна…
Записать ответ.
, равна…
Записать ответ.
 на отрезке
на отрезке  равна
равна  , где
, где  ,
,  (
( - целые числа). Ответ представить в виде:
- целые числа). Ответ представить в виде: 
 плоской фигуры, ограниченной линиями
плоской фигуры, ограниченной линиями 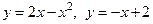 , равен
, равен  , где
, где  (
( - целое число). Ответ представить в виде:
- целое число). Ответ представить в виде: 
 функции
функции  на отрезке
на отрезке  равно
равно  , где
, где  ,
,  (
( - целые числа). Ответ представить в виде:
- целые числа). Ответ представить в виде: 
 равен… Записать ответ.
равен… Записать ответ.
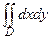 по области
по области  равен
равен  , где
, где  ,
,  (
( - целые числа). Ответ представить в виде несократимой дроби:
- целые числа). Ответ представить в виде несократимой дроби: 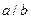
 по области
по области  , ограниченной линиями
, ограниченной линиями  , равен
, равен  , где
, где  ,
,  (
( - целые числа).
Ответ представить в виде:
- целые числа).
Ответ представить в виде: 
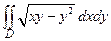 по области
по области  , ограниченной линиями
, ограниченной линиями  равен
равен  , где
, где  (
( - целое число).
Ответ представить в виде:
- целое число).
Ответ представить в виде: 
 ,
,  ,
,  ,
,  ,
, 
 ,
,  ,
,  ,
,  . Формула Ньютона-Лейбница. Несобственные интегралы первого рода (сходимость и расходимость).
. Формула Ньютона-Лейбница. Несобственные интегралы первого рода (сходимость и расходимость).
 равен
равен  , где
, где  ,
,  (
( - целые числа). Ответ представить в виде:
- целые числа). Ответ представить в виде: 
 равен:
1)
равен:
1)  2)
2)  3)
3) 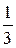 4)
4)  5)
5) 
 . Тогда формула общего члена этого ряда имеет вид:
1)
. Тогда формула общего члена этого ряда имеет вид:
1)  2)
2) 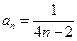 3)
3)  4)
4) 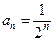
 к ряду
к ряду  , получаем:
1)
, получаем:
1)  2)
2)  3)
3) 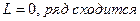 4)
4)  5)
5) 
 сходится по признаку сравнения с рядом
сходится по признаку сравнения с рядом  при:
1)
при:
1)  2)
2)  3)
3)  4)
4)  5)
5) 
 расходится по радикальному признаку Коши, так как
расходится по радикальному признаку Коши, так как  , где
, где  1)
1)  2)
2) 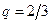 3)
3)  4)
4)  5)
5) 
 сходится по признаку Даламбера, так как
сходится по признаку Даламбера, так как  , где
, где  1)
1)  2)
2)  3)
3)  4)
4)  5)
5) 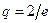
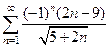 :
1)расходится2)сходится условно 3)сходится абсолютно 4)сходится
:
1)расходится2)сходится условно 3)сходится абсолютно 4)сходится
 В:
В:  cходятся:
1)толькоA 2)только B 3)оба ряда сходятся4)ни один не сходится
cходятся:
1)толькоA 2)только B 3)оба ряда сходятся4)ни один не сходится
 В:
В:  справедливо одно из следующих утверждений:
1) Aсходится абсолютно, Всходится условно
2) Aсходится абсолютно, Всходится абсолютно
3) Aсходится абсолютно, Врасходится
4) Aсходится условно, Всходится условно
5) Aрасходится, Всходится условно
справедливо одно из следующих утверждений:
1) Aсходится абсолютно, Всходится условно
2) Aсходится абсолютно, Всходится абсолютно
3) Aсходится абсолютно, Врасходится
4) Aсходится условно, Всходится условно
5) Aрасходится, Всходится условно
 2: Условно сходится 2:
2: Условно сходится 2:  3: Расходится 3:
3: Расходится 3: 
 разложения функции в ряды Тейлора и Маклорена.
разложения функции в ряды Тейлора и Маклорена.
 равен
равен  . Тогда интервал сходимости этого ряда имеет вид:
1)
. Тогда интервал сходимости этого ряда имеет вид:
1)  2)
2) 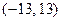 3)
3)  4)
4) 
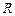 сходимости степенного ряда
сходимости степенного ряда  равен…: Записать ответ.
равен…: Записать ответ.
 является интервал:
1)
является интервал:
1)  2)
2)  3)
3)  4)
4) 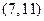 5)
5) 
 , то коэффициент
, то коэффициент  разложения данной функции в ряд Тейлора по степеням
разложения данной функции в ряд Тейлора по степеням  равен…: Записать ответ.
равен…: Записать ответ.
 разложения функции в ряды Тейлора и Маклорена.
разложения функции в ряды Тейлора и Маклорена.
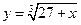 в ряд Маклорена первые три отличные от нуля члена ряда имеют вид
1)
в ряд Маклорена первые три отличные от нуля члена ряда имеют вид
1)  2)
2) 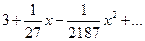 3)
3)  4)
4)  5)
5) 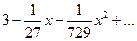
 равно… Записать ответ.
равно… Записать ответ.
 то коэффициент
то коэффициент  разложения данной функции в ряд Тейлора по степеням
разложения данной функции в ряд Тейлора по степеням 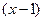 равен…: Записать ответ.
равен…: Записать ответ.
 1:
1:  2:
2: 2:
2:  3:
3:  3:
3:  В ответе указать пары, соответствующих друг другу степенных рядов и их радиусов сходимости.
В ответе указать пары, соответствующих друг другу степенных рядов и их радиусов сходимости.
 является промежуток:
1)
является промежуток:
1)  2)
2)  3)
3)  4)
4)  5)
5) 
 1: знакоположительный
2:
1: знакоположительный
2:  2: знакочередующийся
3:
2: знакочередующийся
3:  3: степенной
В ответе указать пары, соответствующих друг другу рядов и их названий.
3: степенной
В ответе указать пары, соответствующих друг другу рядов и их названий.
 . Дифференциальное уравнение с разделяющимися переменными, линейное ДУ,нахождение их общих и частных решений.
. Дифференциальное уравнение с разделяющимися переменными, линейное ДУ,нахождение их общих и частных решений.
 имеет вид:
1)
имеет вид:
1)  2)
2)  3)
3) 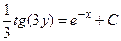 4)
4)  5)
5) 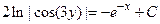
 . Тогда функция
. Тогда функция  является его решением при
является его решением при  равном:
1)
равном:
1)  2)
2)  3)
3)  4)
4)  5)
5) 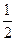
 имеет вид:
1)
имеет вид:
1)  2)
2)  3)
3)  4)
4)  5)
5) 
 имеет вид:
1)
имеет вид:
1)  2)
2)  3)
3)  4)
4) 
 при
при  имеет вид:
1)
имеет вид:
1) 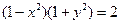 2)
2)  3)
3)  4)
4) 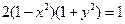
 является:
1)
является:
1)  2)
2)  3)
3)  4)
4)  5)
5) 
 ,
,  . Тогда значение
. Тогда значение  её решения
её решения  равно… Записать ответ.
равно… Записать ответ.
 . Общее и частные решения линейного однородного ДУ второго порядка с постоянными коэффициентами
. Общее и частные решения линейного однородного ДУ второго порядка с постоянными коэффициентами  . Соответствие ОЛДУ второго порядка корням его характеристического уравнения.
. Соответствие ОЛДУ второго порядка корням его характеристического уравнения.
 является функция:
1)
является функция:
1) 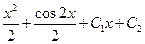 2)
2) 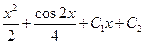 3)
3) 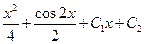 4)
4)  5)
5) 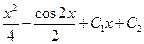
 имеет вид:
1)
имеет вид:
1)  2)
2)  3)
3)  4)
4)  5)
5) 
 при начальных условиях:
при начальных условиях:  имеет вид:
1)
имеет вид:
1)  2)
2)  3)
3) 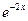 4)
4)  5)
5) 
 1:
1:  2:
2: 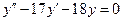 2:
2: 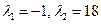 3:
3:  3:
3:  В ответе указать пары, соответствующих друг другу ДУ и корней их характеристических уравнений.
В ответе указать пары, соответствующих друг другу ДУ и корней их характеристических уравнений.
 ), ДУ допускающие понижение порядка (
), ДУ допускающие понижение порядка (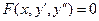 ,
,  ,
,  ), линейные однородные и неоднородные ДУ с постоянными коэффициентами и правой частью специального вида, нахождение их общих и частных решений.
), линейные однородные и неоднородные ДУ с постоянными коэффициентами и правой частью специального вида, нахождение их общих и частных решений.
 . Тогда значение
. Тогда значение  её решения
её решения  равно… Записать ответ.
равно… Записать ответ.
 1:
1:  2:
2:  2:
2:  3:
3:  3:
3:  В ответе указать пары, соответствующих друг другу ДУ и их общих решений.
В ответе указать пары, соответствующих друг другу ДУ и их общих решений.
 неоднородного линейного дифференциального уравнения
неоднородного линейного дифференциального уравнения  имеет вид
имеет вид 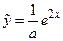 ,где
,где  (
( - целое число).
Ответ записать в виде:
- целое число).
Ответ записать в виде: 
 имеет вид:
1)
имеет вид:
1)  2)
2)  3)
3)  4)
4)  5)
5) 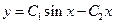
 имеет вид
имеет вид  , где
, где  (
( - целое число). Ответ записать в виде:
- целое число). Ответ записать в виде: 
 неоднородного линейного ДУ:
неоднородного линейного ДУ:  имеет вид
имеет вид  , где
, где 
 (
( - целые числа).
Ответ записать в виде:
- целые числа).
Ответ записать в виде: 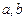
 неоднородного линейного дифференциального уравнения
неоднородного линейного дифференциального уравнения 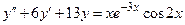 представимо в виде:
1)
представимо в виде:
1)  2)
2)  3)
3)  4)
4)  5)
5) 
 является функция:
1)
является функция:
1)  2)
2)  3)
3)  4)
4)  5)
5) 
 ); допускающее понижение порядка (
); допускающее понижение порядка (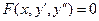 ,
,  ); линейное однородное и неоднородное ДУ порядка
); линейное однородное и неоднородное ДУ порядка  ).
).
 1: линейное
2:
1: линейное
2: 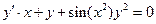 2: Бернулли
3:
2: Бернулли
3:  3: однородное
4:
3: однородное
4:  4: с разделяющимися переменными
В ответе указать пары, соответствующих друг другу ДУ и их названий.
4: с разделяющимися переменными
В ответе указать пары, соответствующих друг другу ДУ и их названий.
 равен…
Записать ответ.
равен…
Записать ответ.
 2)
2)  3)
3)  4)
4) 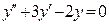 5)
5)  Указать все правильные ответы.
Указать все правильные ответы.


