 |
Методика изучения темы «Объемы пирамиды»
|
|
|
|
На изучение темы «Объем пирамиды» целесообразно отвести три урока.
На первом уроке следует рассмотреть доказательство теоремы об объеме пирамиды. Основная цель данного урока – вывести формулу для нахождения объема пирамиды, показать применение теории к решению задач.
Для этого необходимо предложить ученикам задачи на нахождение площади поверхности пирамиды, вспомнить основные элементы, свойства. Предложить учащимся задачи на нахождение площади основания и т.д.
Используя текст учебника, необходимо подробно разобрать, как получается выражение для площади сечения пирамиды через площадь ее основания:
S(x)= 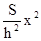 .
.
Вычислить интеграл  учащиеся могут самостоятельно.
учащиеся могут самостоятельно.
Второй урок можно посвятить повторению вопросов теории и решению задач. При подведении итогов урока можно использовать вопросы 4, 5 к главе VII учебника [7], а также задачи:
·
|
|
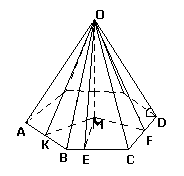
На третьем уроке выводится формула объема усеченной пирамиды как следствие теоремы об объеме пирамиды. В учебнике [7] предлагается вывести эту формулу самостоятельно.
В конце данного урока проводится самостоятельная работа по учебнику [7] контролирующего характера (на 6-8 мин):
|
|
|
Вариант I: задача № 686 (а) для l = 10 см,  = 300.
= 300.
Вариант II: задача № 688(а) для Н = 10 см, 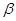 = 600.
= 600.
Можно провести практическую работу (учитывается как контрольная). Учитель заранее подготавливает модели правильных пирамид (4-6) для работы в классе. Модели, покупные или изготовленные учащимися, перенумеровываются и раздаются по одной. Учащийся не получает ту модель, которую он сам изготовил. Учитель имеет готовые ответы. Измерения производятся в см или в мм.
Указания даются устно:
1) Вместо буквы n поставить цифры 4 или 6.
2) Выполнить все необходимые измерения, сделать чертеж, заполнить таблицу.
3) Выражение для вычисления площади основания Q записать.
4) Все вычисления записывать в таблицу.
| Модель №……… Правильная n-угольная пирамида | |
| Сторона основания………………………… Периметр основания………………………. Площадь основания……………………….. Апофема пирамиды……………………….. Площадь боковой поверхности…………… Площадь полной поверхности……………. Высота пирамиды…………………………. Объем пирамиды………………………….. | а (см) Р (см) Q (см) А (см) Sбок (см2) S (см2) Н (см) V (см3) |
Дополнительное задание (подготавливается учителем на карточках и предлагается учащимся):
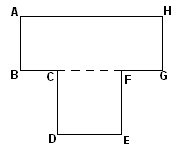
1. По развертке, данной в масштабе, вычислить действительные площадь полной поверхности и объем: 1) правильной призмы (рис. 8); 2) правильной пирамиды (рис. 9)
2.
|
|

Указание: при выполнении в тетради чертежей пирамиды и призмы учащийся может взять произвольные размеры основных элементов.
3. Вычислить объем башни, размеры которой в метрах даны на рисунке 10.
Вывод формулы объема пирамиды в учебнике [7] рассматривается в два этапа (Приложение 7). Вначале автор предлагает рассмотреть для треугольной пирамиды, а затем – для произвольной. Автор проводит ось, рассматривает сечение плоскостью, выражает площадь сечения через площадь основания, применяет основную формулу для вычисления объемов (определенный интеграл). В доказательстве автор также использует признаки подобия. Таким образом, хорошо прослеживается связь с ранее уже изученным.
|
|
|

Следствием теоремы, в отличие от [8], является формула объема для усеченной пирамиды. Доказательства в данном учебнике не приведено. В учебнике [7] формулировка формулы приведена, как задача, причем автор сам задачу решает.
Мы рассмотрели основные рекомендации для изучения данной темы, которые описаны в соответствующей литературе. Но есть и другие приемы и методы, которыми практически не пользуются, но они имеют свои преимущества. Далее приведена примерная (авторская) система данных уроков.
|
Дело в том, что объемы тел – тема, вызывающая достаточно большие трудности у учащихся. В этом разделе есть четыре трудных для усвоения теоремы: 1) об объеме прямоугольного параллелепипеда; 2) об объеме пирамиды; 3) об объеме цилиндра; 4) об объеме тела, полученного вращением криволинейной трапеции [21].
Выводы формул для вычисления объема каждого вида многогранника, цилиндра, конуса проводятся разными методами, что вызывает значительные трудности при их воспроизведении.
Предлагаемая мною система изучения этого раздела устраняет недостатки и создает условия для усвоения основной идеи измерения фигур в пространстве: объем фигуры может быть найден с помощью вычисления интеграла от определенным образом заданной функции.
С целью осуществления такого подхода к измерениям пространственных фигур предлагается посвятить несколько уроков обобщению изученного ранее материала об измерении отрезков и плоских фигур (о длинах и площадях) и ввести аналогичным образом измерение пространственных фигур. Рассмотрим их содержание более подробно.
Урок 1
Тема урока: обобщение свойства длин отрезков и площадей плоских фигур.
Цель урока: повторить свойства длин отрезков и площадей фигур, провести необходимые аналогии.
В начале урока необходимо повторить таблицу метрической системы мер длины, площади и объемов. Для этого удобно заготовить такую таблицу заранее (если ее нет в кабинете) и вывесить ее перед учениками (Приложение 4).
|
|
|
Упражнения для повторения свойств площадей фигур:
1. На рис. 11 изображен отрезок АВ. Найдите длину отрезка АВ, считая единицей измерения: а) сторону одной клетки; б) 1 см (отрезок CD); в) отрезок EF.
При решении этой задачи следует акцентировать внимание учащихся на том, что длина одного и того же отрезка может выражаться разными числами в зависимости от выбора единицы измерения. Но если единица измерения уже выбрана, то длина отрезка есть единственное число. При этом длина отрезка всегда положительна.
2. На рис. 12 изображена плоская фигура ABCDEF. Найдите ее площадь, приняв за единицу измерения: а)половину клетки; б) одну клетку; в) треугольник POQ.
При решении этой задачи следует обратить внимание учащихся на то, что площадь плоской фигуры есть число, которое зависит от выбора единицы измерения. Если единица измерения выбрана, то площадь фигуры единственна. Кроме того, площадь фигуры обязательно неотрицательна, какая бы фигура ни была взята в качестве единицы измерения.
|
|

 Рис. 12
Рис. 12
3. Прямоугольник имеет стороны 5 и 4 см. Какова площадь прямоугольника? Какая фигура выбрана за единицу измерения площадей и какова его площадь?
4.
|

Решая эту задачу, мы пользуемся таким свойством площадей плоских фигур: если плоская фигура разбита на две, общая часть которых есть линия или точка, то площадь всей фигуры равна сумме площадей, ее составляющих.
5.  Треугольники ABC и A1B1C1 конгруэнтны. Площадь
Треугольники ABC и A1B1C1 конгруэнтны. Площадь  ABC равна 36 см2. Какова площадь
ABC равна 36 см2. Какова площадь  A1B1C1?
A1B1C1?
Решив этот комплекс задач, можно сделать выводы, сформулировав их как свойства измерения площадей плоских фигур.
Упражнение для закрепления:
1. Докажите, что два треугольника, на которые диагональ делит параллелограмм, имеют равные площади.
|
|
|
2.Основание прямоугольника в два раза больше его высоты. Покажите на рисунке: а) как нужно разрезать этот прямоугольник на две части, чтобы из них можно было составить прямоугольный треугольник; б) как разрезать его на две части, чтобы из них можно было составить равнобедренный треугольник; в) как разрезать его на три части так, чтобы из них можно было составить квадрат. Что можно утверждать о площадях этих фигур (рис. 14, а-в)?
Урок 2
Тема урока: объем тела.
Цель урока: сформулировать основные свойства объемов.
Измерение объемов пространственных фигур должно удовлетворять свойствам, аналогичным свойствам измерения длин отрезков и площадей плоских фигур.
Учитель формирует следующие свойства.
Каждой пространственному тел ставится в соответствие величина (объем тела), причем это соответствие удовлетворяет следующим условиям:
· объем любого тела неотрицателен;
· конгруэнтные тела имеют равные объемы;
· если тело М есть объединение тел М1 и М2, пересечение которых либо содержит только точки или линии поверхностей обоих тел, либо пусто, то объем тела М равен сумме объемов тел М1 и М2;
· объем куба, длина ребра которого равна 1, равен единице.
Упражнения для закрепления свойств объемов пространственных фигур:
1. Прямоугольный параллелепипед ABCDA1B1C1D1, объем которого 18 см3, разделен сечением KLMN на два конгруэнтных тела (рис. 15). Найдите объем каждой части.
2. Из кубов, длины ребер которых равны 1 см, составлена фигура, изображенная на рис. 16. Вычислите ее объем.
|

4. Прямоугольный параллелепипед ABCDA1B1C1D1 разделен плоскостью АСС1А на две треугольные призмы, объем одной из которых равен 8 см3. Найдите объем параллелепипеда.
|
|


Урок 3
Тема урока: интегральная формула для вычисления объема фигуры.
Цель урока: показать построение подынтегральной функции и способ вычисления объемов фигур с помощью интеграла.
В начале урока в ходе решения ряда упражнений следует напомнить учащимся способ вычисления площадей плоских фигур с помощью интеграла: 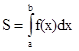 , где f(x) – функция, задающая криволинейную трапецию.
, где f(x) – функция, задающая криволинейную трапецию.
После этого следует сообщить учащимся, что для вычисления объемов пространственных фигур существует аналогичный способ, к изучению которого мы и переходим.
Пусть дана пространственная фигура Ф. Выберем плоскость  таким образом, чтобы она не пересекала Ф (рис. 17).
таким образом, чтобы она не пересекала Ф (рис. 17).
Выберем прямую Ох, перпендикулярную плоскости  . Зададим на этой прямой координаты: за начало координат возьмем О – точку пересечения прямой Ох с плоскостью
. Зададим на этой прямой координаты: за начало координат возьмем О – точку пересечения прямой Ох с плоскостью  . Положительное направление выбрано в том полупространстве, в котором расположена фигура Ф. Через точку с координатой х на этой прямой проведем плоскость
. Положительное направление выбрано в том полупространстве, в котором расположена фигура Ф. Через точку с координатой х на этой прямой проведем плоскость  (х), параллельную плоскости
(х), параллельную плоскости  . Таким образом можно установить соответствие между плоскостями, параллельными плоскости
. Таким образом можно установить соответствие между плоскостями, параллельными плоскости  , и множеством действительных чисел.
, и множеством действительных чисел.
|
|
|
Среди плоскостей данного множества есть такие, которые пересекают фигуру Ф. Первая из этих плоскостей имеет координату а, а последняя – b. Таким образом, фигура Ф заключена между плоскостями  (a) и
(a) и  (b), другими словами, задана на отрезке [a,b]. Конечно, далеко не всегда фигура задана на отрезке. Она может быть задана на интервале, на дискретном множестве и т. п. Но в курсе геометрии средней школы можно ограничиться рассмотрением фигур, заданных на отрезке.
(b), другими словами, задана на отрезке [a,b]. Конечно, далеко не всегда фигура задана на отрезке. Она может быть задана на интервале, на дискретном множестве и т. п. Но в курсе геометрии средней школы можно ограничиться рассмотрением фигур, заданных на отрезке.
Упражнения:
1. Дан куб ABCDA1B1C1D1, длина ребра которого равна 3. В качестве плоскости  выбрана плоскость ABCD, а в качестве Ох – прямая АА1. Найдите значения a и b и укажите плоскости
выбрана плоскость ABCD, а в качестве Ох – прямая АА1. Найдите значения a и b и укажите плоскости  (a) и
(a) и  (b).
(b).
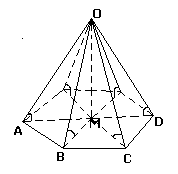
2. Дана пирамида ABCD. В качестве плоскости  выбрана плоскость BCD, а в качестве оси Ох – высота АМ пирамиды. Найдите значения a и b и укажите плоскости
выбрана плоскость BCD, а в качестве оси Ох – высота АМ пирамиды. Найдите значения a и b и укажите плоскости  (a) и
(a) и  (b), если АМ=6.
(b), если АМ=6.
3. Дан шар радиуса 8 см с центром в точке К. В качестве плоскости  выбрана плоскость на расстоянии 10 см от центра шара. Задайте ось Ох, найдите значения a и b и укажите плоскости
выбрана плоскость на расстоянии 10 см от центра шара. Задайте ось Ох, найдите значения a и b и укажите плоскости  (a) и
(a) и  (b).
(b).
4. Постройте функцию S(x) для шара радиуса 8 см, если плоскость  (х) проходит через центр шара.
(х) проходит через центр шара.
5. Постройте функцию S(x) для конуса с высотой Н и радиусом основания R, если в качестве плоскости  выбрана плоскость, параллельная основанию и проходящая через вершину конуса.
выбрана плоскость, параллельная основанию и проходящая через вершину конуса.
После решения этих упражнений формулируется следующее определение: объемом фигуры Ф называется интеграл от a до b функции S(x):  .
.
Упражнения:
6. Запишите интегральную формулу для вычисления объемов фигур, заданных в упр. 4, 5.
7. Запишите формулу для вычисления объема цилиндра высоты Н и радиуса R, если в качестве плоскости  выбрана плоскость основания цилиндра.
выбрана плоскость основания цилиндра.
8. Запишите формулу для вычисления объема прямоугольного параллелепипеда с измерениями m, p, n (плоскость  задайте сами).
задайте сами).
Урок 4
Тема урока: интегральная формула для вычисления объема фигуры.
Цель урока: закрепить изученное на предыдущем уроке и провести доказательство обоснованности данного определения объема.
Упражнения:
1. Выведите формулу для вычисления объема призмы с высотой Н и площадью основания S.
Решение. Здесь a=0, b=H, S(x)=0. Следовательно, 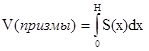 .
.
2. Выведите формулу для вычисления объема пирамиды с высотой Н и площадью основания Q (аналогично тому, как это делалось для конуса).
Решение. Выберем в качестве плоскости  плоскость, параллельную основанию и проходящую через вершину. Тогда а=0, b=H,
плоскость, параллельную основанию и проходящую через вершину. Тогда а=0, b=H, 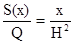 . Поэтому S(x)=
. Поэтому S(x)= 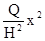 . Следовательно,
. Следовательно, 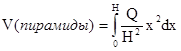 .
.
Так как объемы фигур должны удовлетворять ранее перечисленным свойствам объемов, то надо показать, что при таком определении объема эти свойства выполнены.
Упражнения:
Выпишите интегральные формулы и выведите формулы для вычисления объема:
1. Призмы с высотой Н и площадью основания S.
2. Пирамиды с высотой Н и площадью основания Q.
3. Цилиндра с высотой Н и радиусом основания R.
4. Конуса с высотой Н и радиусом основания R.
5. Шара радиуса R.
После изучения всех формул для нахождения объема тел следует провести проверочную работу в виде теста.
Тест (объем прямоугольного параллелепипеда) [34]
1. Выберите неверное утверждение.
а) За единицу измерения объемов принимается куб, ребро которого равно единице измерения отрезков;
б) тела, имеющие равные объемы, равны;
в) объем прямоугольного параллелепипеда равен произведению трех его измерений;
г) объем куба равен кубу его ребра;
д) объем прямоугольного параллелепипеда равен произведению площади основания на высоту.
2. Найдите объем прямоугольного параллелепипеда, если его длина равна 6 см, ширина – 7 см, а диагональ – 11 см.
а) 252 см3; б) 126 см3; в) 164 см3; г) 462 см3; д) 194 см3.
3. Основанием прямоугольного параллелепипеда служит квадрат, диагональ которого равна 6. Через диагональ основания и противолежащую вершину верхнего основания проведена плоскость под углом 450 к нижнему основанию. Найдите объем параллелепипеда.
а) 108; б) 216; в)27; г)54; д) 81.
4. Стороны основания прямоугольного параллелепипеда равны 5 см и 12 см, диагональ параллелепипеда составляет с плоскостью основания угол 600. найдите объем параллелепипеда.
а) 390 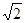 см3; б) 390
см3; б) 390 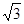 см3; в) 780
см3; в) 780 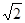 см3; г) 780
см3; г) 780 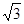 см3; д) 780 см3.
см3; д) 780 см3.
Тест (объем призмы)
1. Сторона основания правильной треугольной призмы равна 2 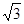 см, а высота – 5 см. найдите объем призмы.
см, а высота – 5 см. найдите объем призмы.
а) 15 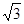 см3; б) 45 см3; в) 10
см3; б) 45 см3; в) 10 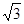 см3; г)12
см3; г)12 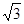 см3; д) 18
см3; д) 18 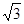 см3.
см3.
2. Выберите неверное утверждение.
а) Объем прямой призмы, основанием которой является прямоугольный треугольник, равен произведению площади основания на высоту;
б) объем правильной треугольной призмы вычисляется по формуле  , где а – сторона основания, h – высота призмы;
, где а – сторона основания, h – высота призмы;
в) объем прямой призмы равен половине произведения площади основания на высоту;
г) объем правильной четырехугольной призмы вычисляется по формуле 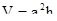 , где а – сторона основания, h – высота призмы;
, где а – сторона основания, h – высота призмы;
д) объем правильной шестиугольной призмы вычисляется по формуле 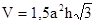 , где а – сторона основания, h – высота призмы.
, где а – сторона основания, h – высота призмы.
3. Основанием прямой призмы является ромб, сторона которого равна 13 см, а одна из диагоналей – 24 см. найдите объем призмы, если диагональ боковой грани равна 14 см.
а) 720 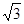 см3; б) 360
см3; б) 360 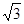 см3; в) 180
см3; в) 180 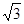 см3; г) 540
см3; г) 540 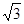 см3; д) 60
см3; д) 60 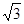 см3.
см3.
4. Основанием прямой призмы служит треугольник со сторонами 10, 10, 12. Диагональ меньшей боковой грани составляет с плоскостью основания угол 600. найдите объем призмы.
а) 480 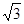 ; б) 960
; б) 960 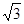 ; в) 240
; в) 240 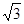 ; г) 480; д) 240.
; г) 480; д) 240.
Тест (объем пирамиды)
1. Объем правильного тетраэдра равен 9 см3. Найдите его ребро.
а) 4 см; б) 2 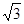 см; в) 3
см; в) 3  см; г) 6 см; д) 3 см.
см; г) 6 см; д) 3 см.
2. Выберите неверное утверждение.
а) объем пирамиды равен произведению одной третьей площади основания на высоту;
б) объем правильного тетраэдра вычисляется по формуле  , где а – ребро тетраэдра;
, где а – ребро тетраэдра;
в) объем усеченной пирамиды, высота которой равна h, а площади основания равны S и M, вычисляется по формуле 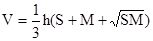
г) объем правильной треугольной пирамиды, ребро которой равно а и все боковые ребра наклонены к плоскости основания под углом  , вычисляется по формуле
, вычисляется по формуле  ;
;
д) объем правильной шестиугольной пирамиды, ребро которой равно а и все боковые ребра наклонены к плоскости основания под углом  , вычисляется по формуле
, вычисляется по формуле  .
.
3. Найдите объем усеченной пирамиды, площади оснований которой равны 3 см2 и 12 см2, а высота равна 2 см.
а) определить нельзя; б) 7 см3; в) 42 см3; г) 14 см3; д) 56 см3.
4. Основанием пирамиды МАВС служит треугольник со сторонами АВ = 5 см, ВС = 12 см, АС = 13 см. Найдите объем пирамиды, если МВ 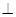 АВС и МВ = 10 см.
АВС и МВ = 10 см.
а) 300 см3; б) 260 см3; в) 780 см3; г) определить нельзя; д) см3.
Углубленное изучение геометрии по учебнику [6]
Рассмотрим методические рекомендации для углубленного изучения темы «Объемы многогранников». В настоящее время для данного обучения в школах используют учебник [6], так как именно он рекомендован (допущен) Министерством образования и науки Российской Федерации к использованию в образовательном процессе в общеобразовательных учреждениях. Теоретический материал учебника разбит на две части – основную и дополнительную. Основная часть содержит теоретические сведения (аксиомы, определения, теоремы); материал, в котором рассказано о значении наиболее важных геометрических результатов, о различных применениях стереометрии в других науках, технике, искусстве, быту, об истории геометрии.
В дополнительном материале с большей глубиной и подробностью обсуждаются самые трудные вопросы курса. Этот материал рассчитан на учащихся, особенно интересующихся математикой.
Глава V данного учебного пособия посвящена объемам тел многогранников. Эта глава традиционная для школьного курса геометрии. И построение ее как будто бы традиционное: сначала выработка общего понятия, затем вывод конкретных формул. Однако есть и характерные отличия.
1. Четко выясняется множество фигур, которые имеют объем в смысле данного определения.
2. Впервые в школьном курсе (и в такой формулировке) дается теорема о существовании и единственности объема.
3. Теорема о представлении объема интегралом рассмотрена с помощью наглядных соображений, так как полное доказательство «сложно и требует расширения понятия интеграла», однако рассуждение приведено тактично и не нарушает уверенности ученика в возможность доказать это утверждение.
4. В данном учебнике выводится формула для нахождения объема наклонного параллелепипеда.
Объем прямого цилиндра
В пункте 26.1 высказаны наглядные соображения, «доказательство математического утверждения с точки зрения физики». С учетом уровня класса можно предположить несколько вариантов дальнейших событий:
а) этим и ограничиться;
б) предложить желающим разобрать пункт 26.2 самостоятельно и ответить индивидуально на оценку;
в) предложить отдельным учащимся сделать сообщение о теореме на уроке. (Для этого теорему можно разбить на 4-5 частей);
г) предложить учащимся разобраться в теореме самостоятельно, а учитель организует по ней семинар в классе;
д) доказать теорему и попросить повторить «сильных» учеников на следующем уроке. И т. д.
Представление объема интегралом
С точки зрения методической представляется более удобным дать формулировку теоремы после доказательства, а сам вывод разбить на четыре части, примерно соответствующие бытовавшему когда-то алгоритму вывода формул и теорем дифференцирования:
1) 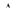 х; 2)
х; 2) 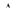 V; 3)
V; 3)  ; 4) V’(x).
; 4) V’(x).
Первый способ рассуждения в теореме более аналитичен, а второй наглядный, и здесь можно «задействовать» теорему о сжатой переменной.
Объемы некоторых тел
Содержание параграфа – независимый вывод формул объемов четырех конкретных видов тел. При желании этот набор можно дополнить выводом формул объемов усеченного конуса (пирамиды) и шарового сегмента. Это позволяет провести с учениками групповую работу. Схема проведения таких работ состоит из нескольких этапов.
I этап. Класс разбивается на группы по шесть человек. Каждому участнику группы дается задание изучить вывод одной из формул (естественно, задания всем в группе различные). Четыре ученика учат пункты § 27, а двое получают от учителя тексты, где выводятся формулы объемов усеченного конуса и шарового сегмента. (Учитель может заменить их другими формулами или вообще не давать других формул, но тогда группа уменьшается до четырех человек и меняется время дальнейшей работы.) Изучив соответствующую теорему, ученик записывает ее в конспект и отыскивает ученика из своей группы, также закончившего запись. Они рассказывают друг другу каждый свою теорему, записывая коротко вывод в конспекте. После этого каждый из них задает вопросы другому и отвечает на его вопросы. После этого пара «распадается», и каждый снова ищет свободного участника своей группы и т. д. На все это уходит два часа. На дом ученики получают задание вывести оставшиеся формулы.
II этап. Продолжается работа в тех же группах (это уже следующий урок геометрии). Однако правила меняются. Теперь каждый получает задание спрашивать вывод какой-то одной из шести формул объема и отвечает спрашиваемому соответственно одну из четырех формул (кроме той, что объяснял на том уроке, и той, что сам спрашивает). За ответ он ставит оценку. На это уходит 1 час.
III этап. И наконец, учитель может на следующем (уже четвертом) уроке вызвать по 1-2 представителя от каждой группы, чтобы по жребию ответить у доски одну из теорем (можно добавить и формулы из домашнего задания). Остальные группы при этом слушают, рецензируют, задают вопросы, добавляют. В итоге каждый ученик оценивается по четырем позициям: 1) запись в конспекте, 2) оценка при ответе товарищу, 3) ответ представителя из группы, 4) качество вопросов и рецензий.
Элемент случайности приносит дополнительную ответственность, игровой момент и компенсируется остальными составляющими оценки [22].
|
|
|


