 |
Арифметические операции над комплексными числами в тригонометрической форме
|
|
|
|
Понятие комплексного числа
1.1 С – множество комплексных чисел
Комплексным числом называется выражение вида 
, где 
и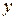 
- действительные числа, 
- мнимая единица (
).
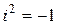Для комплексного числа 
определены модуль и аргумент.
В конце 18 – начале 19 в. Было получено геометрическое истолкование комплексных чисел. Датчанин Г. Вессель, француз Ж. Арган и немец
К. Гаусс независимо друг от друга предложили изображать комплексное число точкой 
на координатной плоскости.
Позже выяснилось, что удобнее изображать число не самой точкой 
, а вектором 
, идущим из начала координат. Тогда вектор можно задавать не только координатами 
и 
, но также длиной 
и углом 
, который он образует с положительным направлением оси абсцисс.
При этом 
, 
, 
, 
(
, 
), 
.
Тригонометрическая форма комплексного числа:
, , 
, 
.
Формула Эйлера: 
.
Показательная форма: 
.
Арифметические операции над комплексными числами
1. Сложение:
.
2. Вычитание:
.
3. Умножение:
.
4. Деление:
.
Арифметические операции над комплексными числами в тригонометрической форме
1. Умножение:
2. Деление:
.
3. Возведение в степень (формула Муавра):
, .
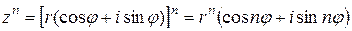4. Извлечение корня
, 
.
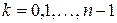2. Понятие функции комплексного переменного
2.1 Область определения и область значения
Пусть даны две плоскости комплексных чисел 
и 
. Рассмотрим некоторое множество точек D в плоскости z и множество G в области w. Если каждому числу 
по некоторому закону поставлено в соответствие определенное комплексное число 
, то говорят, что на множестве D задана однозначная функция комплексного переменного, отражающая множество D во множество G:
Множество D называют областью определения функции f(x).
Если каждая точка множества G является значением функции, то говорят, что G – область значения этой функции (или образ множество D при помощи функции 
). Т.е. функция f отображает D на G.
|
|
|
Функцию 
можно записать в виде:
,
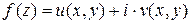где 
, 
– действительные функции, 
.
Если каждому соответствует несколько разных значений w, то функция называется многозначной.
2.2 Предел и непрерывность ФКП
Функция 
имеет предел в точке 
, равный числу 
, если
(2.1)
или
(2.2)
Более подробно свойство (2.1) запишем:
(2.3)
Тогда свойство (2.2) запишем так:
, 
(2.4)
Таким образом, необходимо всюду вместо абсолютной величины писать модуль комплексного число.
Свойства пределов:
1) 
;
2) 
3) 
;
4) 
, 
Эти свойства выполняются, если существуют пределы, стоящие в левых и правых частях равенств.
Функция называется непрерывной в точке z0, если
, 
(2.5)
Таким образом, непрерывная в точке z0 функция должна быть определена в окрестности этой точки, в том числе и в ней самой и должно выполняться равенство (2.5). Это равенство эквивалентно двум равенствам:
и 
(2.6)
Следовательно, непрерывность функции f в точке z 0 эквивалентна непрерывности функций u и v в точке (x 0, y 0).
Функция, непрерывная в каждой точке некоторой области D, называется непрерывной в этой области.
Рассмотрим область D, ограниченную замкнутой не самопересекающейся линией Г.
Эта область называется односвязной.
Если область D ограничена двумя замкнутыми не пересекающимися и не самопересекающимися линиями Г 1и Г 2, то область D называется двусвязной:
Пусть Г 1 – внешняя линия, а Г 2 – внутренняя. Область является двусвязной и в том случае, если линия Г 2 вырождается в точку или в дугу непрерывной линии. Тогда это четырехсвязная область.
3. Производная функция комплексного переменного
Пусть задана однозначная функция на области 
комплексной плоскости 
. Производной от функции в точке называется предел:
где 
любым способом стремится к нулю.
|
|
|
Функцию , имеющую непрерывную производную в любой точке области комплексной плоскости, называют аналитической функцией на этой области.
Степенная функция 
:
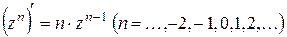
Функция 
при 
аналитическая на всей плоскости , а при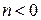 
на всей плоскости с выколотой из неё точкой 
.
Функции 
:
Представим первые три из них как суммы степенных рядов:
Радиус сходимости каждого из этих рядов равен 
. Поэтому производные от этих функций могут быть получены для любых почленным дифференцированием соответствующих рядов:
Функция tgz определяется по формуле:
.
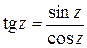Тогда ее производная:
.
Функция a z (a>0)
.
Используя формулу о производной сложной функции
получаем:
.
Гиперболические функции sh z, ch z, th z
.
Кроме того,
.
Тогда получаем тождества:
Производные гиперболических функций:
.
4. Условия Коши – Римана (Даламбера - Эйлера)
Рассмотрим комплексную функцию 
, где 
, определённую на области D комплексной плоскости. Пусть она имеет производную в точке , т.е.:
(4.1)
При этом приращение функции можно записать в виде:
.
Как известно, в пределе (4.1) 
стремиться к нулю любым способом, т.е. возможны два случая:
1) 
и 
;
2) 
и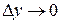 
;
В первом случае: 
.
Во втором случае: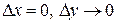 
.
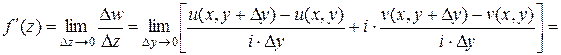
Таким образом, должны выполняться равенства:
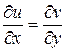и 
.
Эти равенства называют условиями Коши – Римана. Однако эти условия были известны ещё Эйлеру и Даламберу.
Теорема 1: Если функция 
имеет производную в точке 
, то её действительные компоненты u и v имеют в точке 
частные производные первого порядка, удовлетворяющие условиям Коши – Римана.
Теорема 2: Если функции 
и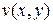 
имеют в точке непрерывные частные производные, удовлетворяющие условиям Коши – Римана, то функция имеет в точке производную.
Из теоремы 1 и 2 вытекает теорема 3.
Теорема 3: Для того, чтобы функция 
была аналитической на области D плоскости z, необходимо и достаточно, чтобы частые производные первого порядка функций u и v были непрерывны на D и выполнялись условия Коши – Римана.
Функции u и v называются сопряжёнными друг к другу на D.
Замечание. Если функцию представить в виде:
,
где R – модуль, Ф – аргумент функции , то условия Кошт – Римана имеют вид:
и 
.
Пример. Проверить выполнение условий Коши – Римана для 
, .
Тогда 
|
|
|
.
.
Таким образом,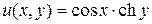 
, 
.
Найдём производные первого порядка:
; 
;
; 
.
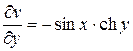Таким образом, условия Коши – Римана выполняются.
Так как частные производные от u и v непрерывны для любых точек , то функция является аналитической на всей комплексной плоскости.
Практика
16.1. Даны комплексные числа 
, 
. Найти:
1) 
,
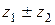2) 
,
3) 
.
1) 
,
,
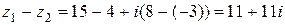2) 
,
3) 
.
16.2. Комплексные числа 
, 
представить в тригонометрической форме и найти:
1) ,
2) ,
3) 
,
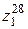4) 
.
1) 
,
,
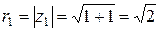тогда 
.
,
,
тогда
.
.
2)
.
3) 
.
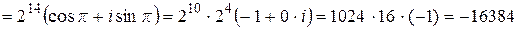4) 
, 
, т.е. 
.
, 
,
, 
,
, 
.
16.3. Комплексные числа , представить в показательной форме.
, 
, 
,
, 
, 
.
16.4. Решить уравнения
а) 
,
.
б) 
,
.
в) 
Пусть 
, тогда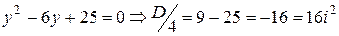 
,
, 
,
т.е.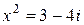 
, 
.
Рассмотрим число 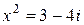в алгебраической форме:
.
При этом 
или 
Приравняем соответствующие действительную и мнимую части:
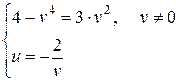
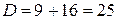
– посторонний корень, т.к. 
и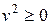 
v 1 = 1 
u 1 = –2; v 2 = –1 u 2 = 2
Получим 2 корня исходного уравнения:
x 1 = –2 + i; x 2 = 2 – i
Рассмотрим число 
.
В алгебраической форме 
, 
. При этом
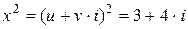или
Составим и решим систему уравнений:
– посторонний корень, т.к. и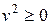
v 3 = 1 u 3 = 2; v 4 = –1 u 4 = –2.
Получим ещё 2 корня исходного уравнения:
x 3 = 2 + i; x 4 = –2 – i
Ответ: x 1 = –2 + i, x 2 = 2 – i, x 3 = 2 + i, x4 = –2 – i.
г) 
По формуле Муавра:
, где 
, 
, 
.
Т.о. 
Тогда, извлекая корень 6-й степени, получаем:
.
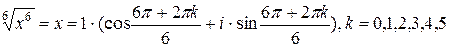k=0: 
k=1:
k=2:
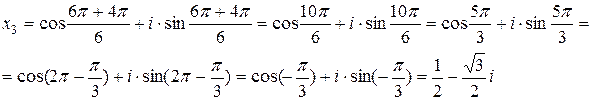
k=3: 
k=4:
k=5:
Ответ: 
, 
, 
, 
, 
, 
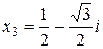ИДЗ № 1
1. Найти все значения корня
1) 
, 
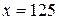Тогда 
2) 
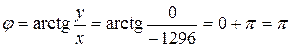
Тогда 
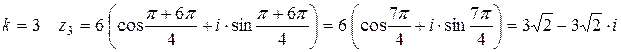
3) 
Тогда 
4) 
Тогда 
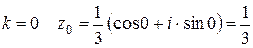
5) 
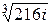
Тогда 
6) 
, 
, 
, 
, 
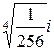
Тогда, 
при 
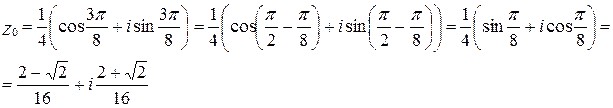
при :
при :
при 
:
7) 
, , 
, 
,
Тогда, 
при :
при :
при :
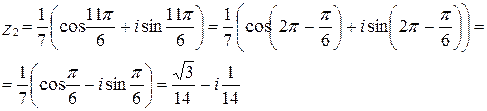
8) 
, 
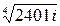
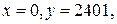
Тогда, 
при :
при :
при : 
при :
9) 
, 
, 
Тогда, 
при : 
при :
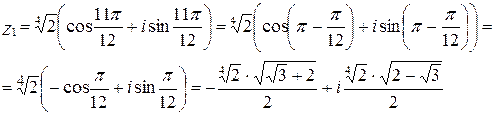
при :
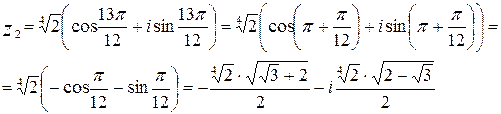
при :
10)
, 
Тогда, 
при :
при :
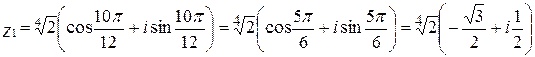
при :
при 
11) 
Тогда, 
при :
при :
при :
при :
12) 
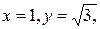
Тогда,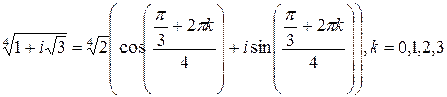 
при
при :
при :
при :
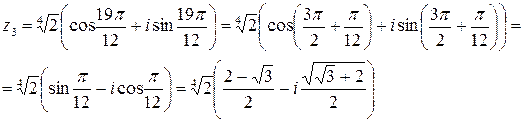
Задача 2. Представить в алгебраической форме
1) 
Многозначный логарифм:
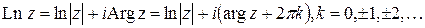
В данном случае, 
, тогда: 
Следовательно, 
При ,получаем главное значение 
2) 
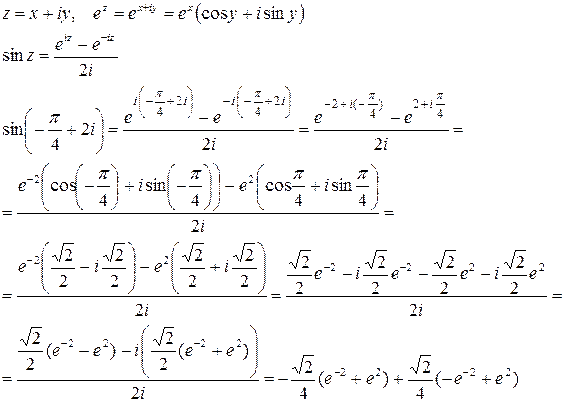
3) 
= 
4) 
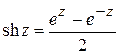
5)
6) 
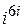
В данном случае: 
, 
.
Тогда 
, 
, следовательно, 
.
|
|
|
При - главное значение 
7) 
, 
, 
.
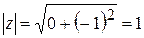При - главное значение 
.
8) 
, 
, 
.
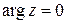При - главное значение 
.
Задача 3. Представить в алгебраической форме.
, 
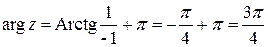
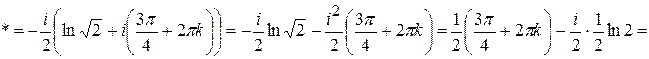
2) 
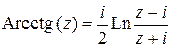
3) 
4) 
5) 
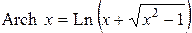
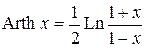
Практика. Дифференцирование ФКП. Условия К-Р
1028. Дифференцируема ли функция 
Имеем 
, 
. Тогда 
, 
. 
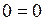- выполняется.
, 
. 
- не выполняется.
Следовательно, функция не дифференцируема.
1030. 
, 
, 
.
, 
.
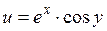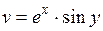
Условия К-Р выполняются.
Найдем производную 
. Для этого можно воспользоваться одной из формул:
(1)
(2)
(1) 
(2) 
1034. Показать, что функция дифференцируема и найти ее производную
; 
.
; 
.
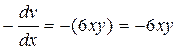1035. Дифференцируема ли функция 
?
; 
.
