 |
Производная сложной функции
|
|
|
|
Пусть  , где
, где  является не независимой переменной, а функцией независимой переменной
является не независимой переменной, а функцией независимой переменной  , т.е.
, т.е.  . Таким образом,
. Таким образом,  .В этом случае функция
.В этом случае функция  называется сложной функцией
называется сложной функцией  ,а переменная
,а переменная  - промежуточным аргументом.
- промежуточным аргументом.
Производная сложной функции находится на основании следующей теоремы: если  и
и  – дифференцируемые функции своих аргументов, то производная сложной функции
– дифференцируемые функции своих аргументов, то производная сложной функции  существует и равна произведению производной функции
существует и равна произведению производной функции  по промежуточному аргументу
по промежуточному аргументу  на производную промежуточного аргумента
на производную промежуточного аргумента  по независимой переменной
по независимой переменной  .
. 
Эта теорема распространяется и несложные функции, которые задаются с помощью цепочки, содержащей три звена и более.
Формулы дифференцирования
С – постоянная,  и
и  функции аргумента
функции аргумента 
1. 
| 4. 
| 7. 
| ||||
2. 
| 5. 
| |||||
3. 
| 6. 
| |||||
| Основные элементарные функции | Сложные функции | |||||
| 1 | 
| 8а | 
| |||
| 2 | 
| 9а | 
| |||
| 3 | 
| 10а | 
| |||
| 4 | 
| 11а | 
| |||
| 5 | 
| 12а | 
| |||
| 6 | 
| 13а | 
| |||
| 7 | 
| 14а | 
| |||
| 8 | 
| 15а | 
| |||
| 9 | 
| 16а | 
| |||
| 10 | 
| 17а | 
| |||
| 11 | 
| 18а | 
| |||
| 12 | 
| 19а | 
| |||
| 13 | 
| 20а | 
| |||
Пример 6. Найти производную функции  .
.
Решение. Данная функция есть алгебраическая сумма функций. Дифференцируем ее, используя формулы 3, 5 и 8: 
Пример 7. Найти производную функции  .
.
Решение: применив последовательно формулы 4, 3, 5 и 8, имеем

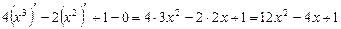 .
.
Пример 8. Найти производную функции  .
.
Решение. Применяя формулы 6, 3, 7 и 1, получим:

Пример 9. Найти производную функции  и вычислить ее значение при
и вычислить ее значение при 
Решение. Это сложная функция с промежуточным аргументом  . Используя формулы 8а и
. Используя формулы 8а и  13, имеем:
13, имеем:  .
.
Вычислим значение производной при  .
.
 .
.
Пример 10. Найти производную функции  .
.
Решение. Используя правило дифференцирования произведения и соответствующие формулы нахождения производных, получим
|
|
|
 .
.
Пример 11. Найти производную функции  .
.
Решение: используя правило дифференцирования частного и соответствующие формулы нахождения производных, получим
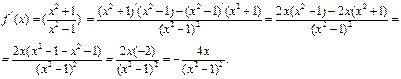
Пример 12. Найти производную функции 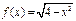 .
.
Решение: полагая  , получим
, получим  .
.

Пример 13. Найти производную функции  .
.
Решение.

Производные высших порядков
Производная функции  в общем случае является функцией от
в общем случае является функцией от  . Если от этой функции вычислять производную, то получим производную второго порядка или вторую производную функции
. Если от этой функции вычислять производную, то получим производную второго порядка или вторую производную функции  .
.
Второй производной функции  называется производная от ее первой производной
называется производная от ее первой производной 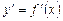 .
.
Вторая производная функции обозначается одним из символов:  ,
,  ,
,  .
.
Аналогично определяются и обозначаются производные любого порядка. Например, производная третьего порядка: 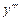 ,
,  ,
,  .
.
Пример 14. Найти вторую производную функции  .
.
Решение. Сначала найдем первую  производную:
производную:
Дифференцируя еще раз, найдем вторую производную:  .
.
Пример 15. Найти вторую производную функции 
Решение. Сначала найдем первую производную этой сложной функции: 
Дифференцируя еще раз, найдем вторую производную: 
Неопределенный интеграл.
Определение: функция F(x) называется первообразной для функции f(x) в промежутке  , если в любой точке этого промежутка ее производная равна f(x):
, если в любой точке этого промежутка ее производная равна f(x):
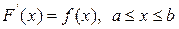 .
.
Определение: совокупность первообразных для функции f(x) называется неопределенным интегралом и обозначается символом  . Таким образом,
. Таким образом, 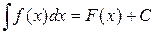 .
.
Здесь f(x) - подынтегральная функция,  - подынтегральное выражение, С – произвольная постоянная.
- подынтегральное выражение, С – произвольная постоянная.
Основные свойства неопределенного интеграла.
1 Если функция 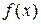 имеет первообразную, то
имеет первообразную, то 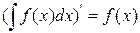 ,
,  .
.
2 Если 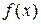 - дифференцируемая функция, то
- дифференцируемая функция, то  ,
,  .
.
3 Если функция 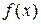 имеет первообразную, то при
имеет первообразную, то при  верно равенство
верно равенство  .
.
4 Если функция 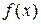 и
и  имеют первообразные, то
имеют первообразные, то  .
.
Таблица неопределенных интегралов.
1.  при при 
| 2. 
|
3. 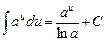
| 4. 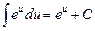
|
5. 
| 6. 
|
7. 
| 8. 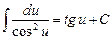
|
9. 
| 10. 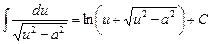
|
11. 
| 12. 
|
13. 
| 14. 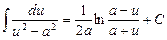
|
Пример 16. Для функции  , найти первообразную F(x), график которой проходит через точку (2;2).
, найти первообразную F(x), график которой проходит через точку (2;2).
|
|
|
Решение: так как при всех  верно равенство
верно равенство  то
то  - одна из первообразных функции
- одна из первообразных функции  . Следовательно,
. Следовательно,  С – некоторая постоянная. Постоянную С находим из условия F(2)=2, то есть
С – некоторая постоянная. Постоянную С находим из условия F(2)=2, то есть  откуда
откуда  . Значит,
. Значит,  .
.
Пример 17. Найти интеграл 
 .
.
Решение:  .
.
Пример 18. Найти интеграл 
 .
.
Решение: 
Пример 19. Найти интеграл 
 .
.
Решение: так как  , то
, то  .
.
Пример 20. Найти интеграл  .
.
Решение: так как  , то
, то  .
.
Пример 21. Найти интеграл  .
.
Решение: так как  , то
, то  .
.
Пример 22. Найти интеграл 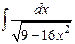 .
.
Решение: 
Определенный интеграл.
Пусть функция  определена на отрезке
определена на отрезке  . Разобьем этот отрезок на n частей точками
. Разобьем этот отрезок на n частей точками  , выберем на каждом элементарном отрезке
, выберем на каждом элементарном отрезке  произвольную точку
произвольную точку  и обозначим через
и обозначим через  длину каждого такого отрезка.
длину каждого такого отрезка.
Определение. Интегральной суммой для функции  на отрезке
на отрезке  называется сумма вида
называется сумма вида  .
.
Определение. Определенным интегралом от функции  на отрезке
на отрезке  называется предел интегральной суммы при условии, что длина наибольшего из элементарных отрезков стремится к нулю:
называется предел интегральной суммы при условии, что длина наибольшего из элементарных отрезков стремится к нулю:  .
.
Для любой функции  , непрерывной на отрезке
, непрерывной на отрезке  , всегда существует определенный интеграл
, всегда существует определенный интеграл 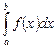 .
.
Для вычисления определенного интеграла от функции  в том случае, когда можно найти соответствующий неопределенный интеграл
в том случае, когда можно найти соответствующий неопределенный интеграл  , служит формула Ньютона – Лейбница:
, служит формула Ньютона – Лейбница:  , то есть определенный интеграл равен разности значений первообразной при верхнем и нижнем пределах интегрирования.
, то есть определенный интеграл равен разности значений первообразной при верхнем и нижнем пределах интегрирования.
При вычислении определенного интеграла методом замены переменной (способом подстановки) определенный интеграл 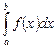 преобразуется с помощью подстановки
преобразуется с помощью подстановки 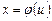 в определенный интеграл относительно новой переменной
в определенный интеграл относительно новой переменной  . При этом старые пределы интегрирования
. При этом старые пределы интегрирования  и
и  , которые находятся из исходной подстановки:
, которые находятся из исходной подстановки:  ,
,  . Таким образом, имеем
. Таким образом, имеем 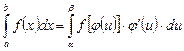 .
.
Пример 23. Вычислить определенный интеграл:  .
.
Решение:
 .
.
Пример 24. Вычислить определенный интеграл:  .
.
Решение:  .
.
Пример 25. Вычислить определенный интеграл: 
 .
.
 .
.
Пример 26. Вычислить определенный интеграл:  .
.
Решение:  .
.
Пример 27. Вычислить определенный интеграл:  .
.
Решение: положим  , тогда
, тогда  ,
,  . Вычисляем новые пределы интегрирования:
. Вычисляем новые пределы интегрирования:  ,
,  . Поэтому
. Поэтому
 .
.
Пример 28. Вычислить определенный интеграл:  .
.
Решение: преобразуем подкоренное выражение:  . Положим
. Положим  , откуда
, откуда  . Найдем новые пределы интегрирования:
. Найдем новые пределы интегрирования:  ,
,  . Следовательно,
. Следовательно,
 .
.
|
|
|
Задания.
№№ 1– 30. Даны числа:  ,
,  . Найдите
. Найдите  .
.
| № | 
| 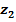
| № | 
| 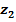
|

| 
| 
| 
| ||

| 
| 
| 
| ||

| 
| 
| 
| ||
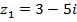
| 
| 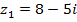
| 
| ||
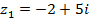
| 
| 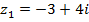
| 
| ||

| 
| 
| 
| ||

| 
| 
| 
| ||

| 
| 
| 
| ||
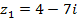
| 
| 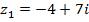
| 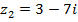
| ||

| 
| 
| 
| ||

| 
| 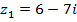
| 
| ||

| 
| 
| 
| ||

| 
| 
| 
| ||

| 
| 
| 
| ||
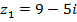
| 
| 
| 
|
№№ 31– 60. Вычислить  и
и  , если
, если
| № | 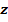
| № | 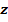
| № | 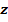
|

| 
| 
| |||

| 
| 
| |||

| 
| 
| |||

| 
| 
| |||

| 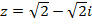
| 
| |||

| 
| 
| |||

| 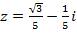
| 
| |||

| 
| 
| |||

| 
| 
| |||
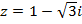
| 
| 
|
№№ 61– 90. Найти производные функции
| № | № | ||
а) 
| а) 
| ||
б) 
| б) 
| ||
а) 
| а) 
| ||
б) 
| б) 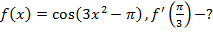
| ||
а) 
| а) 
| ||
б) 
| б) 
| ||
а) 
| а) 
| ||
б) 
| б) 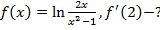
| ||
а) 
| а) 
| ||
б) 
| б) 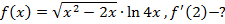
| ||
а) 
| а) 
| ||
б) 
| б) 
| ||
а) 
| а) 
| ||
б) 
| б) 
| ||
а) 
| а) 
| ||
б) 
| б) 
| ||
а) 
| а) 
| ||
б) 
| б) 
| ||
а) 
| а) 
| ||
б) 
| б) 
| ||
а) 
| а) 
| ||
б) 
| б) 
| ||
а) 
| а) 
| ||
б) 
| б) 
| ||
а) 
| а) 
| ||
б) 
| б) 
| ||
а) 
| а) 
| ||
б) 
| б) 
| ||
а) 
| а) 
| ||
б) 
| б) 
|
№№ 91– 120. Найти неопределенный интеграл.
| № | |||
а) 
| б) 
| в) 
| |
а) 
| б) 
| в) 
| |
а) 
| б) 
| в) 
| |
а) 
| б) 
| в) 
| |
а) 
| б) 
| в) 
| |
а) 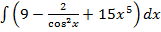
| б) 
| в) 
| |
а) 
| б) 
| в) 
| |
а) 
| б) 
| в) 
| |
а) 
| б) 
| в) 
| |
а) 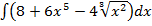
| б) 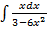
| в) 
| |
а) 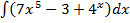
| б) 
| в) 
| |
а) 
| б) 
| в) 
| |
а) 
| б) 
| в) 
| |
а) 
| б) 
| в) 
| |
а) 
| б) 
| в) 
| |
а) 
| б) 
| в) 
| |
а) 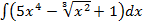
| б) 
| в) 
| |
а) 
| б) 
| в) 
| |
а) 
| б) 
| в) 
| |
а) 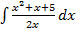
| б) 
| в) 
| |
а) 
| б) 
| в) 
| |
а) 
| б) 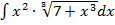
| в) 
| |
а) 
| б) 
| в) 
| |
а) 
| б) 
| в) 
| |
а) 
| б) 
| в) 
| |
а) 
| б) 
| в) 
| |
а) 
| б) 
| в) 
| |
а) 
| б) 
| в) 
| |
а) 
| б) 
| в) 
| |
а) 
| б) 
| в) 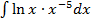
|
№№ 121– 150. Вычислить определенный интеграл.
а) 
| б) 
| |
а) 
| б) 
| |
а) 
| б) 
| |
а) 
| б) 
| |
а) 
| б) 
| |
а) 
| б) 
| |
а) 
| б) 
| |
а) 
| б) 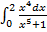
| |
а) 
| б) 
| |
а) 
| б) 
| |
а) 
| б) 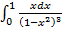
| |
а) 
| б) 
| |
а) 
| б) 
| |
| а) | ||
|
|
|


