 |
Задание №4. Анализ остатков.
|
|
|
|
1. По линии тренда из задания №2 посчитать прогнозные значения для всех 60 (61) дней.
2. Вычислить погрешность (ошибку) прогноза на каждый день.
3. Проверить ошибки на нормальность, пользуясь критерием Пирсона, по следующей методике:
· Весь диапазон наблюдений разбить на не менее, чем k = 3,22*ln (n) +1 равный интервал (число интервалов должно быть целое число!), n – число наблюдений.
· Определим крайние точки интервалов и их средины в порядке возрастания
· Подсчитаем, число попавших в каждый интервал точек, используя функцию ЧАСТОТА.
· Построим таблицу
| Границы интервала | Средины интервала | Практические частоты | Теоретические частоты |
Теоретические частоты ni* вычисляются по следующей формуле
ni* = nhφ(Si*),
φ(Si*) ={ exp [ - (Si* - a)2/(2σ2)] }/(2πσ2)0,5
где a среднее значение всей выборки остатков, σ2 выборочная дисперсия всей выборки остатков, Si*средина интервала i- го интервала, h длина интервала.
· Проверить полученную выборку на «нормальность» по критерию
Пирсона: χ2 =∑(ni*- ni)2/ (ni*)
Результат сравниваем с табличным значением, которое можно найти с помощью функции ХИ2ОБР с уровнем значимости 0,95.
· Построить на одном графике теоретические и практические частоты (для их визуального сравнения).
· Вычислить асимметрию A и эксцесс E для массива ошибок из n данных и сделать по ним заключение о «нормальности» распределения.
Если распределение нормально, то должны выполняться одновременно неравенства:
│A│< 1,5 σA, │E + 6/(n+1)│< 1,5 σE, где
σ2A = 6(n-2)/((n+1)(n+3)), σ2E = 24n(n-2) (n-3),/((n+1)2(n+3)(n+5)).
4. Проверить остатки на стационарность по двухвыборчному F-тесту для дисперсии и двухвыборчному t-тесту для среднего.
|
|
|
5. Написать отчет по проведенной работе.
Для сдачи Задания №3 должны быть выполнены все пункты 1-4. Студент должен ответить на следующие вопросы:
1. Что такое линия тренда?
2. Что такое нормальное распределение? Формулы и экономический смысл.
3. Что такое распределение Хи - квадрат?
4. Что такое асимметрия и эксцесс? Экономический смысл.
5. Для чего надо анализировать остатки? См. [1] стр.193
.
Задание №5. Регрессия, автокорреляция и гетероскедастичность.
1) По тесту Дарбина –Уотсона выяснить имеет ли место автокорреляция остатков первого порядка с достоверностью 0,95.
a. d = =∑(ei-1- ei)2/(∑ (ei)2)
2) Проанализировать остатки на автокорреляцию второго, третьего и т.д. порядков
3) По тесту Голдфельда –Квандта провести проверку на гетероскедастичность.
4) Проанализировать остатки на наличие гетероскедастичности по тесту Уайта.
5) Объяснить причину возникновения автокорреляции с точки зрения экономики. Объяснить, как можно избавиться от автокорреляции с помощью сезонной составляющей или построением регрессии скользящего среднего.
6) Если имеет место гетероскедастичность, то объяснить, как от нее можно избавиться обобщенным методом наименьших квадратов.
7) Пишется отчет с эконометрическим обоснованием выбора линии тренда. Это делается на основе заданий №№1-4.
Для сдачи Задания №4 должны быть выполнены все пункты задания. Студент должен ответить на следующие вопросы:
1. Что такое гетероскедастичность и автокорреляция. Причины возникновения этих явлений. Как они влияют на статистические оценки.
2. Уметь пользоваться таблицами Дарбина –Уотсона
Задание №6. Построение сезонной составляющей (скользящей средней) или уравнения авторегрессии.
Отчет
(набирается в редакторе WORD и сдается на дискете при сдаче зачета. Отчет должен быть не менее двух стандартных страниц шрифт 14 New Roman, поля по 1,5 см с каждой стороны, интервал между строками 1,5 и состоять из следующих разделов:
|
|
|
· Название (например: Изучение курса акций РАО ЕС за октябрь-ноябрь 2003г. ФИО выполнявших студентов полностью
· Исходные данные по акциям в виде таблицы
· Краткий анализ хозяйственной деятельности компании (берется из задания№1)
· Эконометрическое обоснование выбора уравнений Делается на основе заданий 1-4 и включает все основные пункты обоснования:
1. выбор уравнения,
2. проверка его значимости,
3. остатки и их анализ с помощью теоремы Гаусса-Маркова
1. исследования остатков на нормальность
Для получения зачета нужно:
· выполнит задания №№1-5.
· В электронном виде сдать отчет.
· исправить все замеченные преподавателем неточности.
· Принести зачетную книжку.
ГЛАВА 5. СИСТЕМЫ ЭКОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
Теоретические основы
Сложные экономические процессы описывают с помощью системы взаимосвязанных (одновременных) уравнений. Различают несколько видов систем уравнений:
Ø Система независимых уравнений - когда каждая зависимая переменная у рассматривается как функция одного и того же набора факторов х:
Для решения этой системы и нахождения ее параметров используется метод наименьших квадратов;
Ø Система рекурсивных уравнений - когда зависимая переменная у одного уравнения выступает в виде факторах в другом уравнении:
Для решения этой системы и нахождения ее параметров используется метод наименьших квадратов;
Ø Система взаимосвязанных (совместных) уравнений - когда одни и те же зависимые переменные в одних уравнениях входят в левую часть, а в других - в правую:
Такая система уравнений называется структурной формой модели.
Эндогенные переменные - взаимозависимые переменные, которые определяются внутри модели (системы) у.
Экзогенные переменные - независимые переменные, которые определяются вне системы х.
Предопределенные переменные - экзогенные и лаговые (за предыдущие моменты времени) эндогенные переменные системы.
Коэффициенты а и b при переменных - структурные коэффициенты модели.
Система линейных функций эндогенных переменных от всех предопределенных переменных системы - приведенная форма модели:
|
|
|
где 
- коэффициенты приведенной формы модели.
Идентификация – это единственность соответствия между приведенной и структурной формами модели.
С позиции идентифицируемости структурные модели можно подразделить на три вида:
1) идентифицируемые;
2) неидентифицируемые;
3) сверхидентифицируемые.
Модель идентифицируема, если все структурные ее коэффициенты определяются однозначно, единственным образом по коэффициентам приведенной формы модели, т. е. если число параметров структурной модели равно числу параметров приведенной формы модели. В этом случае структурные коэффициенты модели оцениваются через параметры приведенной формы модели и модель идентифицируема.
Модель неидентифицируема, если число приведенных коэффициентов меньше числа структурных коэффициентов, и в результате структурные коэффициенты не могут быть оценены через коэффициенты приведенной формы модели.
Модель сверхидентифицируема, если число приведенных коэффициентов больше числа структурных коэффициентов. В этом случае на основе коэффициентов приведенной формы можно получить два или более значений одного структурного коэффициента. В этой модели число структурных коэффициентов меньше числа коэффициентов приведенной формы. Сверхидентифицируемая модель в отличие от неидентифицируемой модели практически решаема, но требует для этого специальных методов исчисления параметров.
Структурная модель всегда представляет собой систему совместных уравнений, каждое из которых требуется проверять на идентификацию. Модель считается идентифицируемой, если каждое уравнение системы идентифицируемо. Если хотя бы одно из уравнений системы неидентифицируемо, то и вся модель считается неидентифицируемой. Сверхидентифицируемая модель содержит хотя бы одно сверхидентифицируемое уравнение.
Выполнение условия идентифицируемости модели проверяется для каждого уравнения системы. Чтобы уравнение было идентифицируемо, необходимо, чтобы число предопределенных переменных, отсутствующих в данном уравнении, но присутствующих в системе, было равно числу эндогенных переменных в данном уравнении без одного.
|
|
|
Если обозначить число эндогенных переменных в 
-м уравнении системы через 
, а число экзогенных (предопределенных) переменных, которые содержатся в системе, но не входят в данное уравнение, — через 
, то условие идентифицируемости модели может быть записано в виде следующего счетного правила:
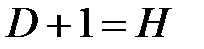
| уравнение идентифицируемо |
| уравнение неидентифицируемо |
| уравнение сверхидентифицируемо |
Для оценки параметров структурной модели система должна быть идентифицируема или сверхидентифицируема.
Если необходимое условие выполнено, то далее проверяется достаточное условие идентификации.
Достаточное условие идентификации. Уравнение идентифицируемо, если определитель матрицы, составленной из коэффициентов при переменных, отсутствующих в исследуемом уравнении, не равен нулю, и ранг этой матрицы не менее числа эндогенных переменных системы без единицы.
Коэффициенты структурной модели могут быть оценены разными способами в зависимости от вида системы одновременных уравнений. Наибольшее распространение в литературе получили следующие методы оценивания коэффициентов структурной модели:
1) косвенный метод наименьших квадратов;
2) двухшаговый метод наименьших квадратов;
3) трехшаговый метод наименьших квадратов;
4) метод максимального правдоподобия с полной информацией;
5) метод максимального правдоподобия при ограниченной информации.
Рассмотрим вкратце сущность каждого из этих методов.
Косвенный метод наименьших квадратов (КМНК) применяется в случае точно идентифицируемой структурной модели. Процедура применения КМНК предполагает выполнение следующих этапов работы.
1. Структурная модель преобразовывается в приведенную форму модели.
2. Для каждого уравнения приведенной формы модели обычным МНК оцениваются приведенные коэффициенты 
.
3. Коэффициенты приведенной формы модели трансформируются в параметры структурной модели.
Если система сверхидентифицируема, то КМНК не используется, ибо он не дает однозначных оценок для параметров структурной модели. В этом случае могут использоваться разные методы оценивания, среди которых наиболее распространенным и простым является двухшаговый метод наименьших квадратов (ДМНК).
Основная идея ДМНК – на основе приведенной формы модели получить для сверхидентифицируемого уравнения теоретические значения эндогенных переменных, содержащихся в правой части уравнения.
|
|
|
Далее, подставив их вместо фактических значений, можно применить обычный МНК к структурной форме сверхидентифицируемого уравнения. Метод получил название ДМНК, ибо дважды используется МНК: на первом шаге при определении приведенной формы модели и нахождении на ее основе оценок теоретических значений эндогенной переменной 
и на втором шаге применительно к структурному сверхидентифицируемому уравнению при определении структурных коэффициентов модели по данным теоретических (расчетных) значений эндогенных переменных.
Сверхидентифицируемая структурная модель может быть двух типов:
1) все уравнения системы сверхидентифицируемы;
2) система содержит наряду со сверхидентифицируемыми точно идентифицируемые уравнения.
Если все уравнения системы сверхидентифицируемые, то для оценки структурных коэффициентов каждого уравнения используется ДМНК. Если в системе есть точно идентифицируемые уравнения, то структурные коэффициенты по ним находятся из системы приведенных уравнений
Решение типовых задач
Пример 1
Требуется:
1. Оценить следующую структурную модель на идентификацию:
2. Исходя из приведенной формы модели уравнений
найти структурные коэффициенты модели.
Решение
1. Модель имеет три эндогенные (у1, у2, уз) и три экзогенные (х1, х2, х3) переменные.
Проверим каждое уравнение системы на необходимое (Н) и достаточное (Д) условия идентификации.
Первое уравнение.
Н: эндогенных переменных - 2 (у 1 у3),
отсутствующих экзогенных - 1 (х2).
Выполняется необходимое равенство: 2 =1 + 1, следовательно, уравнение точно идентифицируемо.
Д: в первом уравнении отсутствуют у2 и х2 - Построим матрицу из коэффициентов при них в других уравнениях системы:
| Уравнение | Отсутствующие переменные | |
| y2 | х2 | |
| Второе | -1 | а22 |
| Третье | b32 |
Det А = -1 ∙ 0 – b32 ∙a22 ≠ 0.
Определитель матрицы не равен 0, ранг матрицы равен 2; следовательно, выполняется достаточное условие идентификации, и первое уравнение точно идентифицируемо.
Второе уравнение.
Н: эндогенных переменных - 3 (у1, у2, уз),
отсутствующих экзогенных - 2 (х1,x3)
Выполняется необходимое равенство: 3 = 2 + 1, следовательно, уравнение точно идентифицируемо.
Д: во втором уравнении отсутствуют xi и х3. Построим матрицу из коэффициентов при них в других уравнениях системы:
| Уравнение | Отсутствующие переменные | |
| x1 | x з | |
| Первое | а11 | а13 |
| Третье | а31 | а33 |
Det А = а11 ∙ а33 - а31 ∙ а13 ≠ 0.
Определитель матрицы не равен 0, ранг матрицы равен 2, следовательно, выполняется достаточное условие идентификации, и второе уравнение точно идентифицируемо.
Третье уравнение.
Н: эндогенных переменных - 2 (у2, у3),
отсутствующих экзогенных - 1 (х 2).
Выполняется необходимое равенство: 2=1 + 1, следовательно, уравнение точно идентифицируемо.
Д: в третьем уравнении отсутствуют у1 и х2. Построим матрицу из коэффициентов при них в других уравнениях системы:
| Уравнение | Отсутствующие переменные | |
| у1 | x2 | |
| Первое | -1 | |
| Второе | b21 | а22 |
DetA = -l a22 - b2l 0 ≠ 0.
Определитель матрицы не равен 0, ранг матрицы равен 2, следовательно, выполняется достаточное условие идентификации, и третье уравнение точно идентифицируемо.
Следовательно, исследуемая система точно идентифицируема и может быть решена косвенным методом наименьших квадратов.
2. Вычислим структурные коэффициенты модели:
1) из третьего уравнения приведенной формы выразим х2 (так как его нет в первом уравнении структурной формы):
Данное выражение содержит переменные уз, х1 и х3, которые нужны для первого уравнения структурной формы модели (СФМ). Подставим полученное выражение х2 в первое уравнение приведенной формы модели (ПФМ):
2) во втором уравнении СФМ нет переменных х1 и х3. Структурные параметры второго уравнения СФМ можно будет определить в два этапа:
Первый этап: выразим х1 в данном случае из первого или третьего уравнения ПФМ. Например, из первого уравнения:
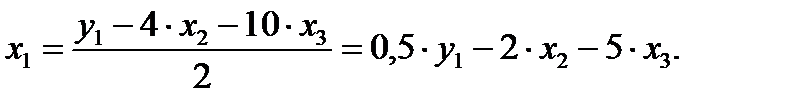
Подстановка данного выражения во второе уравнение ПФМ не решило бы задачу до конца, так как в выражении присутствует х3, которого нет в СФМ.
Выразим х3 из третьего уравнения ПФМ:
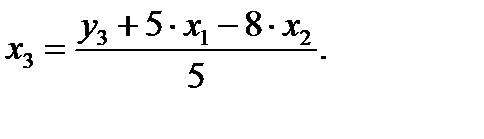
Подставим его в выражение х1:
Второй этап: аналогично, чтобы выразить х3 через искомые у1, у3 и х2, заменим в выражении хз значение х1 на полученное из первого уравнения ПФМ:
Следовательно,
x3 = 0,033 ∙ у3 + 0,083 ∙ у1 – 0,6 ∙ x2.
Подставим полученные х1 и хз во второе уравнение ПФМ:
Это уравнение можно получить из ПФМ иным путем. Суммируя все уравнения, получим
Далее из первого и второго уравнений ПФМ исключим х1 домножив первое уравнение на 3, а второе - на (-2) и просуммировав их:
Затем аналогичным путем из полученных уравнений исключаем х3, а именно:
3) из второго уравнения ПФМ выразим х2, так как его нет в третьем уравнении СФМ:
Подставим полученное выражение в третье уравнение ПФМ:
Таким образом, СФМ примет вид
Пример 2
Изучается модель вида
где у - валовой национальный доход;
y-1 - валовой национальный доход предшествующего года;
С - личное потребление;
D - конечный спрос (помимо личного потребления);
ε1 и ε2 - случайные составляющие.
Информация за девять лет о приростах всех показателей дана в табл. 3.1.
Таблица 5.1
| Год | D | y-1 | у | С | Год | D | y-1 | у | С |
| -6,8 | 46,1 | 3,1 | 7,4 | 44,7 | 17,8 | 37,2 | 8,6 | ||
| 22,4 | 3,1 | 22,8 | 30,4 | 23,1 | 37,2 | 35,7 | 30,0 | ||
| -17,3 | 22,8 | 7,8 | 1,3 | 51,2 | 35,7 | 46,6 | 31,4 | ||
| 12,0 | 7,8 | 21,4 | 8,7 | 32,3 | 46,6 | 56,0 | 39,1 | ||
| 5,9 | 21,4 | 17,8 | 25,8 | Σ | 167,5 | 239,1 | 248,4 | 182,7 |
Для данной модели была получена система приведенных уравнений:
Требуется:
1. Провести идентификацию модели.
2. Рассчитать параметры первого уравнения структурной модели.
Решение:
1. В данной модели две эндогенные переменные (у и С) и две экзогенные переменные (D и y-1). Второе уравнение точно идентифицировано, так как содержит две эндогенные переменные и не содержит одну экзогенную переменную из системы. Иными словами, для второго уравнения имеем по счетному правилу идентификации равенство: 2=1 + 1.
Первое уравнение сверхидентифицировано, так как в нем на параметры при С и D наложено ограничение: они должны быть равны. В этом уравнении содержится одна эндогенная переменная у. Переменная С в данном уравнении не рассматривается как эндогенная, так как она участвует в уравнении не самостоятельно, а вместе с переменной D. В данном уравнении отсутствует одна экзогенная переменная, имеющаяся в системе. По счетному правилу идентификации получаем: 1 + 1 = 2: D + 1 > Н. Это больше, чем число эндогенных переменных в данном уравнении, следовательно, система сверх-идентифицирована.
2. Для определения параметров сверхидентифицированной модели используется двухшаговый метод наименьших квадратов.
Шаг 1. На основе системы приведенных уравнений по точно идентифицированному второму уравнению определим теоретические значения эндогенной переменной С. Для этого в приведенное уравнение
С = 8,636 + 0,3384 ∙ D + 0,2020 ∙ y-1
подставим значения D и y-1, имеющиеся в условии задачи. Получим:
1 = 15,8; 
2 = 16,8; 3 = 7,4; 4 = 14,3; 5 = 15,0; 6 = 27,4;
7 = 24,0; 8 = 33,2; 9 = 29,0.
Шаг 2. По сверхидентифицированному уравнению структурной формы модели заменяем фактические значения С на теоретические и рассчитываем новую переменную С + D (табл. 3.2).
Таблица 5.2
| Год | D |
|
+ D
| Год | D |
|
+ D
|
| -6,8 | 15,8 | 9,0 | 44,7 | 27,4 | 72,1 | ||
| 22,4 | 16,8 | 39,2 | 23,1 | 24,0 | 47,1 | ||
| -17,3 | 7,4 | -9,9 | 51,2 | 33,2 | 84,4 | ||
| 12,0 | 14,3 | 26,3 | 32,3 | 29,0 | 61,3 | ||
| 5,9 | 15,0 | 20,9 | Σ | 167,5 | 182,9 | 350,4 |
Далее к сверхидентифицированному уравнению применяется метод наименьших квадратов. Обозначим новую переменную
+ D через Z. Решаем уравнение
y = a1 + b1 ∙ Z.
Система нормальных уравнений составит:
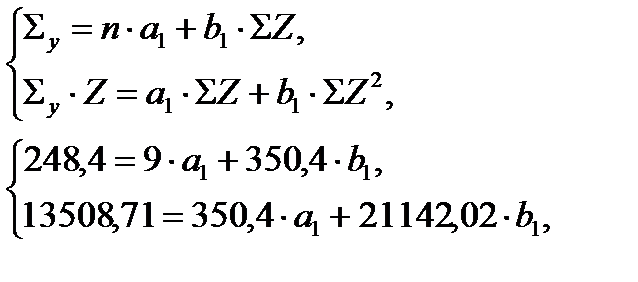
а1 = 7,678; b1 = 0,512.
Итак, первое уравнение структурной модели будет таким:
У = 7,678 + 0,512 ∙ (С + D).
Пример 3
Имеются данные за 1990-1994 гг. (табл. 3.3).
Таблица 5.3
| Год | Годовое потребление свинины на душу населения, фунтов, y1 | Оптовая цена за фунт, долл., у2 | Доход на душу населения, ДОЛЛ., x1 | Расходы по обработке мяса, % к цене, x2 |
| 5,0 | ||||
| 4,0 | ||||
| 4,2 | ||||
| 5,0 | ||||
| 3,8 |
Требуется:
Построить модель вида
рассчитав соответствующие структурные коэффициенты.
Решение:
Система одновременных уравнений с двумя эндогенными и двумя экзогенными переменными имеет вид
В каждом уравнении две эндогенные и одна отсутствующая экзогенная переменная из имеющихся в системе. Для каждого уравнения данной системы действует счетное правило 2 = 1 + 1. Это означает, что каждое уравнение и система в целом идентифицированы.
Для определения параметров такой системы применяется косвенный метод наименьших квадратов.
С этой целью структурная форма модели преобразуется в приведенную форму:
в которой коэффициенты при х определяются методом наименьших квадратов.
Для нахождения значений δ11 и δ12 запишем систему нормальных уравнений:
При ее решении предполагается, что х и у выражены через отклонения от средних уровней, т. е. матрица исходных данных составит:
| y1 | y2 | x1 | x2 | |
| -3 | 0,6 | -200 | ||
| -1 | -0,4 | -200 | -1 | |
| -0,2 | -1 | |||
| -1 | 0,6 | |||
| -0,6 | -7 | |||
| Σ | 0,0 |
Применительно к ней необходимые суммы оказываются следующими:
Σу1х1 = 1600; Σу1х2 = -37; Σx21 = 180 000;
Σx1х2 = - 1900; Σx22 = 96.
Система нормальных уравнений составит:
Решая ее, получим:
δ11 = 0,00609; δ12 = -0,26481.
Итак, имеем y1 =0,00609 • x1 - 0,26481 • х2.
Аналогично строим систему нормальных уравнений для определения коэффициентов δ21 и δ22:
Следовательно,
δ21 =0,00029; δ22 =0,11207,
тогда второе уравнение примет вид
y2 = 0,00029 • x1 + 0,11207 • х2.
Приведенная форма модели имеет вид
Из приведенной формы модели определяем коэффициенты структурной модели:
Итак, структурная форма модели имеет вид
Вопросы по главе
1. Что понимается под системой независимых уравнений?
2. Что понимается под системой рекурсивных уравнений?
3. Что понимается под системой взаимосвязанных (совместных) уравнений?
4. Что называется эндогенными переменными?
5. Что называется экзогенными переменными?
6. Что называется предопределенными переменными?
7. Что понимается под приведенной формой модели?
8. Какими бывают структурные модели с точки зрения идентифицируемости?
9. Какая модель является идентифицируемой?
10. Какая модель является неидентифицируемой?
11. Какая модель является сверхидентифицируемой?
12. В чем заключается правило идентифицируемости модели?
13. Чем простой МНК отличается от косвенного МНК?
14. В чем состоит суть двухшагового метода наименьших квадратов?
ЗАКЛЮЧЕНИЕ [1]
К 1930-м годам сложились все предпосылки для выделения эконометрики в отдельную науку. Стало ясно, что для более глубокого понимания экономических процессов стоит использовать в той или иной степени статистику и математику. Возникла необходимость появления новой науки со своим предметом и методом, объединяющая все исследования в этом направлении. 29 декабря 1930 г. по инициативе И. Фишера, Р. Фриша, Я. Тинбергена, Й. Шумпетера, О. Андерсона и других ученых было создано эконометрическое общество. В 1933 г. Р. Фриш основал журнал «Эконометрика», который и сейчас имеет большое значение для развития эконометрики. А уже в 1941 г. появляется первый учебник по новой научной дисциплине, написанный Я. Тинбергеном. В 1969 г. Фриш и Тинберген стали первыми исследователями получившими Нобелевскую премию по экономике. Как говорится в официальном сообщении нобелевского комитета: «за создание и применение динамических моделей к анализу экономических процессов».
До 1970-х годов эконометрика понималась как эмпирическая оценка моделей, созданных в рамках экономической теории. По мнению эконометристов того времени, статистические данные должны были защитить теорию от догматизма. При этом подавляющее большинство экономических моделей, построенных в этот период, были кейнсианскими. Но, начиная с 1970-х годов, формальные методы стали использоваться при выборе причинности теоретических концепций. При этом эконометрикой стали активно пользоваться и монетаристы.
В 1980 г. вторую эконометрическую Нобелевскую премию по экономике получил американский экономист Лоуренс Клейн за создание экономических моделей и их применение к анализу колебаний экономики и экономической политики. Совместно с А. Голдбергом создал одну из самых известных моделей американской экономики, известной как «модель Клейна–Голдберга». В основу структуры этой модели были положены его собственные разработки. Она состояла из взаимосвязанных одновременных и направленных рядов уравнений, решение которых давало картину производства в стране. Говоря об этой модели, Р.Дж. Болл отмечал: «Как эмпирическое представление об основах кейнсианской системы эта модель стала, возможно, самой знаменитой среди моделей крупных национальных хозяйств до появления других моделей в 60-е гг.»[9]. Клейн также организовал широко известный проект «Линк» для интеграции статистических моделей разных стран в единую общую систему с целью улучшения понимания международных экономических связей и прогнозирования в области мировой торговли. В это время активно развивалась не только макро-, но микроэконометрика. Пионерами этого направления выступили Д. Хэкман и Д. Макфадден. Они разработали теорию и методы, которые широко используются в статистическом анализе поведения индивидуумов и домохозяйств как в экономике, так и в других общественных науках. Так, Дж. Хекман решил проблему смещения выборки из-за селективности данных и самоотбора. Для ее решения он предложил использовать метод коррекции Хекмана, который благодаря своей эффективности и простоте в использовании стал широко использоваться в эмпирических исследованиях. Основной вклад Д. Макфаддена в науку заключается в развитии методов для анализа дискретного выбора. В 1974 г. он разработал условный логит-анализ, который сразу был признан фундаментальным достижением экономической науки. Также он создал эконометрические методы для оценки производственных технологий и исследования факторов, лежащих в основе спроса фирм на капитал и рабочую силу. Выдающиеся достижения этих ученых были отмечены Нобелевской премией по экономике в 1990 г.
Важным событием для развития эконометрики стало появление компьютеров. Благодаря им мощное развитие получил статистический анализ временных рядов. Г. Бокс и Г. Дженкинс создали ARIMA-модель в 1970 г., а К. Симс и некоторые другие ученые — VAR-модели в начале 1980-х гг. Стимулировало эконометрические исследования и бурное развитие финансовых рынков и производных инструментов. Это привело лауреата Нобелевской премии по экономике за 1981 год Дж. Тобина к разработке моделей с использованием цензурированных данных.
Большое влияние на современную эконометрику оказал и Хаавельмо. Хаавельмо показал, как можно использовать методы математической статистики для того, чтобы получать обоснованные заключения о сложных экономических взаимосвязях исходя из случайной выборки эмпирических наблюдений. Эти методы можно, кроме того, использовать для оценивания соотношений, полученных на основе экономических теорий, и для проверки этих теорий. В 1989 г. ему присудили Нобелевскую премию по экономике «за прояснение вероятностных основ эконометрики и анализ одновременных экономических структур».
Хаавельмо рассматривал экономические ряды как реализацию случайных процессов. Главными проблемами, возникающими при работе с такими данными являются нестационарность и сильная волатильность. Если переменные нестационарны, то есть риск установить связь там, где ее нет. Вариантом решения данной проблемы является переход от уровней ряда к их разностям. Недостатком данного метода является сложность экономической интерпретации полученных результатов. Для решения этой проблемы Клайв Грэнджер ввел концепцию коинтеграции как стационарной комбинации между нестационарными переменными. Им была предложена модель корректировки отклонений (ЕСМ), для которой он разработал методы оценивания ее параметров, обобщения и тестирования. Коинтеграция применяется в случае, если краткосрочная динамика отражает значительные дестабилизирующие факторы, а долгосрочная стремится к экономическому равновесию. Модели, созданные Грэнджером, в 1990 г. были обобщены С. Йохансеном для многомерного случая. В 2003 г. Гренджер совместно с Р. Инглом получили нобелевскую премию. Р. Ингл, в свою очередь, известен как создатель моделей с меняющейся во времени волатильностью (т. н. ARCH-модели). Эти модели получили широкое распространение на финансовых рынках.
Сегодня эконометрика занимает достойное место в ряду экономических наук. В мире выпускается ряд научных журналов, полностью посвященных эконометрике, в том числе: Journal of Econometrics (Швеция), Econometric Reviews (США), Econometrica (США), Sankhya. Indian Journal of Statistics. Ser.D. Quantitative Economics (Индия), Publications Econometriques (Франция). Эконометрику изучают в ведущих мировых университетах, пришло понимание, что без эконометрических методов невозможно проводить современный макро- и микроэкономический анализ.
На русском языке также существуют специализированные журналы. К ним относятся «Прикладная эконометрика» и «Квантиль». Отдельные публикации по эконометрике появляются в журналах «Экономика и математические методы», «Вопросы статистики», «Вопросы экономики» и некоторых других.
Ранее в России по ряду причин эконометрика не была сформирована как самостоятельное направление научной и практической деятельности. Хотя в настоящее время начинают развертываться эконометрические исследования. В связи с этим начинается широкое преподавание этой дисциплины.
СПИСОК ЛИТЕРАТУРЫ
Основная литература
1. Елисеева, И.И. Эконометрика: Учебник. 2-ое изд. / Под ред. И.И. Елисеевой. – М.: Финансы и Статистика, 2007. – 576 с.
2. Елисеева, И.И., Практикум по Эконометрике / Под редакцией И.И. Елисеевой. – М.: Финансы и Статистика, 2004. – 192 с.
3. Шанченко, Н.И. Эконометрика: лабораторный практикум/ Н.И. Шанченко. – Ульяновск: УлГТУ, 2004. – 81с.
4. Шишов, В.В. Принятие оптимальных экономических решений: учебное пособие/ В.В
|
|
|
