Биматричная игра: сущность, привести экономический пример.

Основные понятия и определения теории антагонистических игр

Антагонистическая игра - модель конфликтной ситуации в игре двух участников с прямо противоположными интересами: игра, моделирующая экономическую ситуацию противостояния, противоборства, конкуренции двух сторон с взаимно противоположными интересами.

Антагонистическиеигры (далее А. и.) — игры, в которых участвуют два игрока (обычно обозначаемые I и II) с противоположными интересами. Для А. и. характерно, что выигрыш одного игрока равен проигрышу другого и наоборот, поэтому совместные действия игроков, их переговоры и соглашения лишены смысла. Большинство азартных и спортивных игр с двумя участниками (командами) можно рассматривать как А. и. Принятие решений в условиях неопределённости, в том числе принятие статистических решений, также можно интерпретировать как А. и. Определяются А. и. заданием множеств стратегий игроков и выигрышей игрока I в каждой ситуации, состоящей в выборе игроками своих стратегий. Таким образом, формально А. и. есть тройка ‹ А, В, Н›, в которой А и В — множества стратегий игроков, а Н (а, b) — вещественная функция (функция выигрыша) от пар (а, b), где а Î A, b Î В. Игрок I, выбирая а, стремится максимизировать Н (а, b),а игрок II, выбирая b, — минимизировать Н (а, b). А. и. с конечными множествами стратегий игроков называются матричными играми.

Основой целесообразного поведения игроков в А. и. считается принцип минимакса. Следуя ему, I гарантирует себе выигрыш

точно так же II может не дать I больше, чем

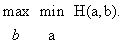
Если эти "минимаксы" равны, то их общее значение называется значением игры, а стратегии, на которых достигаются внешние экстремумы, — оптимальными стратегиями игроков. Если "минимаксы" различны, то игрокам следует применять смешанные стратегии, т. е. выбирать свои первоначальные ("чистые") стратегии случайным образом с определёнными вероятностями. В этом случае значение функции выигрыша становится случайной величиной, а её математическое ожидание принимается за выигрыш игрока I (соответственно, за проигрыш II). В играх против природы оптимальную смешанную стратегию природы можно принимать как наименее благоприятное априорное распределение вероятностей её состояний. В А. и. игроки, используя свои оптимальные стратегии, ожидают получения (например, в среднем, если игра повторяется многократно) вполне определённых выигрышей. На этом основан рекуррентный подход к динамическим играм в тех случаях, когда они сводятся к последовательностям А. и., решения которых можно найти непосредственно (например, если эти А. и. являются матричными). А. и. составляют класс игр, в которых принципиальные основы поведения игроков достаточно ясны. Поэтому всякий анализ более общих игр при помощи А. и. полезен для теории.

Биматричная игра: сущность, привести экономический пример.

Биматричная игра - конечная бескоалиционная игра двух лиц. Биматричная игра задается двумя матрицами одинакового размера , являющимися матрицами выигрышей соответственно игроков I и II. Стратегией игрока I является выбор строки матриц, стратегией игрока II - выбор столбца. Если игрок I выбирает , а игрок II выбирает 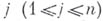, то они получают соответственно выигрыши и , Если для всех то биматричная игра является матричной игрой.

Пример: «Борьба за рынки». Небольшая фирма (игрок А) намерена сбыть партию товара на одном из двух рынков, контролируемое другой, более крупной фирмой (игрок В) Для этого фирма А готова предпринять но одном из рынков соответствующие приготовления (например, развернуть рекламную компанию). Господствующая на рынках фирма В может пытаться воспрепятствовать этому, приняв на одном из рынков предупредительные меры (разумеется, в рамках закона). Не встречая противодей­ствия на рынке, фирма А захватывает его; при наличии препятствий — терпит поражение.

Будем считать для определенности, что проникновение фирмы А на первый рынок более выгодно для нее, нежели проникновение на второй. Естественно также считать, что и борьба за первый рынок потребует вложения больших средств. Например, победа фирмы А на первом рынке принесет ей вдвое больший выигрыш, чем победа на втором, но зато и поражение при попытке освоиться на первом рынке полностью ее разорит, а фирму В избавит от конкурента.

Что же касается второго рынка, то при поражении фирмы А ее потери будут не столь разорительны, но и победа принесет немного.

Таким образом, у фирмы А два стратегии:

А ₁ — выбор первого рынка, А ₂ — выбор второго рынка.

Такие же стратегии и у фирмы В:

В ₁ — выбор первого рынка, В ₂ — выбор второго рынка.

Для того, чтобы составить платежные матрицы игроков, нужны расчетные количественные показа­тели, которые мы приведем здесь в условных единицах:

,

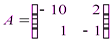Взглянем на выписанные матрицы выплат. Из сказанного выше ясно, что если оба игрока выберут один и тот же рынок, то победа останется за более сильной фирмой В.

То, что в ситуации (А ₁, В ₁) выигрыш игрока В равен 5, а в ситуации (А ₂, В ₂) — 1, подчерки­вает, что первый рынок более выгоден (удобно расположен, хорошо посещаем и т.п.), чем второй. Выигрыш (-10) игрока А в ситуации (А ₁, В ₁) (а точнее, проигрыш) в сопоставлении с его выигры­шем (-1) в ситуации (А ₂, В ₂) выглядит, разумеется, вполне сокрушительно. Что же касается ситуации, когда фирмы уделяют основное внимание разным рынкам (А ₁, В ₂) и (А ₂, В ₁), то здесь фирму А ждет настоящий выигрыш, больший на более выгодном рынке. Потери, которые при этом несет фирма В, оказываются прямо противоположными.

53. Критерий существования седловых точек действительной функции двух векторных аргументов

Для того, чтобы f(x,y) имела седловую точку(оптимальное решение игры) на декартовом произведении X*Y, необходимо и достаточно, чтобы существовали и были равны , где – это точная нижняя граница множества значений функции (т.е. наибольшая из бесконечного множества нижних границ множества значений функции ), а – это точная верхняя граница множества значений функции (т.е. наименьшая из бесконечного множества верхних границ множества значений функции ).