Б. Параболическая аппроксимация.

РЕГРИССИОННЫЙ АНАЛИЗ (АППРОКСИМАЦИЯ РАЗЛИЧНЫХ ЗАВИСИМОСТЕЙ)

 

Одной из областей практического приложения статистических методов рас­чета является аппроксимация различных зависимостей, задаваемых числами. Обычно с этой целью график искомой зависимости y=f (х) строят в линейном, логарифмическом или ином масштабе, что по его виду позволяет оценить закон изменения величины у (х). Такой процесс трудоемок, а главное, не обеспечивает предельно высокой точности аппроксимации.

Согласно известному методу наименьших квадратов условие максимальной приближенности реальной зависимости Y = f (X), задан­ной числами, к аппроксимирующей ее функции, заданной аналитически, совпадает с условием минимума суммы квадратов погрешностей для всех дис­кретных значений у_п = f (x_n). Формулы, позволяющие найти параметры ап­проксимирующей зависимости по ряду ее приближенных дискретных значений Yп =f(X_n) полученные на основе метода наименьших квадратов, даны в математической литературе. Рассмотрим реализацию таких расчетов в электронных таблицах при любом числе дискретных значений х_п и у_п.

А. Линейная аппроксимация.

Пусть дано N пар точек х_п, у_п, приближен­но представляющих линейную зависимость у = b0 + b1X, (1)

где b_о — отрезок, отсекаемый прямой у = f (х) на оси у; b1 — угловой коэффициент этой прямой. Тогда b_о и b1 определяются следующим образом –

Рис. 1. К линейной регрессии

в облаке точек Xi, Yi плоскости х-у (рис. 5.4) требуется провести прямую так, чтобы величина всех отклонений отвечала условию

 

 

где Y(Xi) – зависимость (1). Для этого нужно приравнять к нулю частные производные:

 

что дает для определения неизвестных коэффициентов b0 и b1 систему линейных уравнений. Решение этой системы дает искомые коэффициенты аппроксимации:

(2)

 

Рассмотрим практический пример. Пусть преобразователь напряжения U в частоту F имеет зависимость F (U), заданную значениями:

Тогд а в соответствии с формулами (2) следует рассчитать следующие суммы:

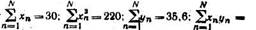
Расчет дает b_о = 4,75 кГц; b1= 0,395 кГц/В

Следовательно, аппроксимирующая прямая выражается формулой:

F= 4,75 + 0,395U,

где F в килогерцах, U- в вольтах.

Используя суммы, легко можно подсчитать коэффициент парной корреляции R или среднеквадратичной погрешности:

N N N

σ= [Σ Yi² – b1*ΣYi –b0*Σ(Xi*Yi)]/N (3)

i=1 i= i=1

 

Б. Параболическая аппроксимация.

Пусть между X и Y существует нелинейная зависимость в виде параболы:

Yр = a*X² +b*X +c. (4)

В этом случае для нахождения коэффициентов a, b и c (аналитической формулы зависимости Yi от Xi), необходимо решить довольно громоздкую систе­му линейных алгебраических уравнений:

 

(5)

 

Система уравнений (5) является следствием применения метода наименьших квадратов для расчета коэффициентов аппроксимации.

Работу следует выполнять в следующем порядке:

■ Рассчитать таблицу для полу­чения коэффициентов и правых ча­стей системы линейных уравнений (4), позволяющей найти коэффици­енты параболы а, b, с аппроксими­рующей зависимость Y_i от Х_i.

■ Записать матрицы коэффициентов и правых частей. Коэффициенты при неизвестных а, b, с и правые части это различные суммы (например, сумма всех Х_i или Xi*Yi). Они берутся из строки «Сумма», а коэффициент «n» -это количество точек в таблице задающей зависимость Y_iот Xi. Найти фор­мулу для Y_p, отыскав коэффициенты параболы, путём решения системы линейных уравнений методом «Обратной матрицы», предполагающего получение обратной матрицы и вычесления её произведения с правой частью системы уравнений (4).

· Заполнить таб­лицу, включающую в себя графы: X, Y, Yp, взяв X и Y из задания, и рассчитав Yp для каждого X по получен­ной формуле.

· Создать диаг­рамму точечного типа, содержащую график «Экспериментальные точки» с зависимос­тью Y от X в виде то­чек и график «Расчёт­ные значения» с зави­симостью Y_p от X в виде линий без марке­ров.

Вариант выполнения задания приведен на рис.2.

 

 

Рис.2.

 

 

 

Дополнительная информация по работе с матрицами:

Наиболее распространён­ными функциями, позво­ляющими работать с матрица­ми являются:

• МОБР(массив) - Возвращает обратную матри­цу для матрицы, хранящейся в массиве.

Массив - это числовой массив с равным количеством строк и столбцов. Массив может быть задан как диапазон ячеек, например, А1:СЗ; как массив констант, например, {1;2;3: 4;5;6: 7;8;9} или как имя диапазона или масси­ва. При использовании массива констант для разделения чисел в строке используется «;» а для разделения строк «:». Если какая-либо из ячеек в массиве пуста или содержит текст, а также если массив имеет неравное число строк и столбцов, то функция МОБР возвращает ошибку #ЗНАЧ!.

В каче­стве примера того, как вычисляется обратная матрица, рассмотрим, приве­дённый на рис.3 массив из трёх строк и трёх столбцов А2:С4, который содержит коэффициенты при неизвестных системы линейных уравнений (исходная матрица). После выделения области для ответа -А6:С8 и выпол­нения команды: МОБР(А2:С4) в ней появляется матрица обратная исход­ной.

• МУМНОЖ(массив1;массив2) - Возвращает произведение матриц (матрицы хранятся в массивах).

Результатом является массив с таким же числом строк, как массив 1, и с таким же числом столбцов, как массив 2. Массив1, массив2 - это перемножаемые массивы. Количество столбцов аргумента массив 1 должно быть таким же, как количество сток аргумента массив 2, и оба массива должны содержать только числа. Массив 1 и массив2 могут быть заданы как интервалы, массивы констант или ссылки. Если хотя бы одна ячейка в аргументах пуста или содержит текст, или если число столбцов в аргументе массив 1 отличается от числа строк в аргументе массив2, то функция МУМНОЖ возвращает ошибку #ЗНАЧ!.

Например, про­изведение двух двумерных массивов приводит к образованию такого же двумерного массива, т.е. МУМН0Ж({1; 3: 7; 2}; {2; 0: 0; 2}) равняется {2; 6: 14; 4}, а при умножении двумерного на одномерный получается одно­мерный массив МУМНОЖ({3; 0: 2; 1}; (2:1}) равняется {6; 5}. А в случае МУМН0Ж({1: 3; 0: 7; 2; 0: 1; 0; 0}; {2; 0: 0; 2}) вместо ответа появляется сообщение об ошибке #ЗНАЧ!, поскольку первый массив имеет три столб­ца, а второй массив имеет только две строки.

Чаще всего приведённые две функции используются для решения сис­тем линейных уравнений с несколькими неизвестными методом «Обрат­ной матрицы». Причём сначала вычисляется матрица, обратная матрице коэффициентов при неизвестных, а затем она умножается на матрицу пра­вых частей системы. Результатом этого умножения является матрица зна­чений неизвестных.

 

 

На рис.3 приведена система трёх линейных уравнений с тремя неизве­стными и её решение методом обратной матрицы. Для этого сначала в ячейки А2:С4 были введены значения коэффициентов при неизвестных, а в ячейки Е2:Е4 правые части уравнения. Затем найдена обратная матрица, для этого выделена область для ответа - ячейки А6:С8 и выполнена коман­да МОБР(А2:С4). Полученную обратную матрицу умножают на матрицу правых частей, предварительно выделив область для ответа - ячейки Е6:Е8. В верхней части рис.3 изображена "панель функций", на которой отобра­жена функция МУМНОЖ с введёнными значениями аргументов, следует заметить, что для получения правильного ответа в поле «Массив 1» записы­вается адрес обратной матрицы, а в поле «Массив2» - адрес матрицы пра­вых частей. Теперь для получения ответа нужно одновременно нажать на три клавиши “Ctrl+Shift+Enter”. Таким образом создастся и выполнится команда МУМНОЖ(A6:C8;E2:E4).

 

 

Поделиться:

Воспользуйтесь поиском по сайту: