 |
Построение графиков функций с помощью дифференциального исчесления:асимптоты.
|
|
|
|
Вопрос 52. Теорема Коши.
Теорема:
Пусть 
и 
непрерывны на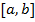 
и дифф. на 
и при этом 
на (a, b) 
т. с 
(a, b) такая, что 
, где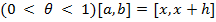 
Док-во:
= 
Это действительно так, т.к. если 
, то по т. Ролля 
А это противоречит условиям теоремы. Функция определена и непрерывна на 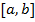и дифф. на
функция 
удовлетворяет условиям т. Ролля и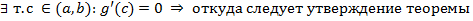 
, где 
Пусть = x
Вопрос 53. Теорема о производной константы, монотонной и строго монотонной ф-ии. Достаточный признак монотонности ф-ий.
Теорема 1:
Для того, чтобы дифф. на пром-ке X ф-ия 
была const <Н> и <Д>, чтобы 
выполнялось внутри X.
Док-во:
<Н> мы уже доказали, когда установили, что производная константы = 0.
<Д> из следствия 1 теоремы Лагранжа.
Теорема 2:
Пусть имеет конечную производную на промежутке X. 
Для того, чтобы была монотонно возрастающей, убывающей на пр-ке Х <Н> и <Д> условие 
.
Док-во:
<Н> Пусть например возрастает на Х. Пусть 
- внутренняя точка пр-ка Х
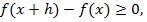при 
и 
при 
.
Но мы видим, что в обоих случаях 
ну а тогда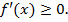 
<Д> Пусть 
на X. Возьмем 
Надо показать, что тогда
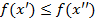
Рассмотрим 
применим теорему Лагранжа 
где 
Теорема 3:
Для того, чтобы дифф. на Х ф-ия была строго возр. или убыв. <Н> и <Д> выполнить условия:
1) 
2) 
не обращается тождественно в 0 на любом 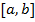принадл. Х
Док-во:
<Н> Пусть строго возрастающая, тогда по теореме 2 на про-ке Х 
т. е. условие 1 выполняется.
Пусть условие 2 не выполняется, ну а тогда по теореме 1 оказывается, что = const на 
что противоречит строгому возрастанию функции на Х.
<Д> Пусть выполняется 1) и 2) из условия 1 следует, что - возрастает на мно-ве Х, это следует из теоремы 2, следовательно, для 
из Х; 
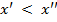
если 
Надо показать, что 
Пусть это не так, т. е. тождественная const на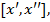 
что противоречит условию 2.
|
|
|
Из 1) и 2) следует, что строго возрастает на Х.
Из теорем 1, 2, 3 вытекает достаточный признак строгой монотонности ф-ии, который удобен в приложениях.
Теорема 4:
Если 
на пром-ке Х за исключением разве лишь конечного числа точек этого промежутка 
- строго возрастающая (убывающая) на Х.
Вопрос 54. Приращение дифф. функции. Теорема о дифф. суперпозиции.
Теорема 1:
Пусть f(x) - дифф. в т. x, тогда её приращение 
при достаточно малых |h| представима = f’(x) 
h + 
, где 
Док-во:
По условию f(x) дифф. в т. x 
существует конечная f’(x): f’(x)=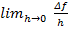 
Пусть 
= f’(x) - 
во-первых: = f’(x) h +
во-вторых:
Теорема 2:
Пусть 
- суперпозиция ф-ии g и f(x). Пусть ф-ии 
является дифф. в т. х, а 
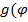) - является дифф. в точке . Тогда - дифф. в т. х
Док-во:
По усл. и 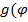) являются непрерывными
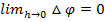
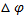=0
И для обеих ф-ий выполняются равенства (1)
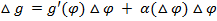
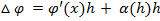
Рассмотрим 
Рассмотрим 
(
)’= 
= 
Примеры:
Вопрос 55. Производные высших порядков, их свойства. Формула Лейбница.
Пусть y=f(x) дифф. на X, z=f’(x) определена на Х и мы можем говорить о её производной в некоторой точке х принад. Х, если производная z существует в точке х, то её называют второй производной функции f(x) в точке х.
И т. д.
И по индукции мы можем определить производную функции для любого n принад. N и мы получим, что
- это и есть производная n-го порядка.
Примеры:
Опр2:
Если функция f(x) имеет на мн-ве Х производные порядка n включительно, то говорят, что f(x) дифф. n-раз на Х.
Рассмотрим теперь св-ва n-раз дифф. ф-ий
Пусть y = f(x) и z = g(x) - это n-раз дифф. на некотором множестве ф-ии:
1) 
(по индукции из определения производной n-го порядка)
2) Рассмотрим 
, тогда имеет место формула Лейбница:
Докажем формуле по мат. индукции:
Вопрос 56. Теорема Тейлора: остаточные члены разложения ф-ии в формах Лагранжа и Коши.
Теорема 1:
Пусть f(x) дифф. n-раз на сегменте [a,b]
Пусть n = b - a, тогда имеет место следующая формула:
|
|
|
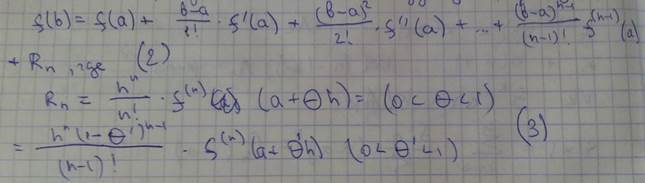
Док-во:
Вопрос 57. Теорема Лопиталя: применение теоремы для раскрытия неопределенностей
Теорема1:
Пусть f(x) n-раз непрерывно дифф. в точке а и выполняются f(a)=0, f’(a)=0... 
(a)=0
Пусть g(x) n-раз непрерывно дифф. в точке а и выполнаются: g(a)=0, g’(a)=0... 
Тогда,
Док-во:
Примеры:
БИЛЕТ 58.
Построение графиков функций с помощью дифференциального исчесления:асимптоты.
Определение1(определение наклонной асимптоты): прямая y=ax+b называется наклонной асимптотой кривой y=f(x), если lim[f(x)-ax-b]=0 (x->+-∞)
Из этого определения в частности следует, что lim[f(x)/x]=a (x->+∞)
Lim[f(x)-ax]=b (x->+∞)
Геометрически асимптота занимает то предельное положение, к которому стремится касательная к кривой в точке (x,f(x)) при х -> +∞
Определение2: прямая x=c, т.е. параллельная оси Оу, называется вертикально асимптотой кривой y=f(x) /(x<c) (/-знак сужения)
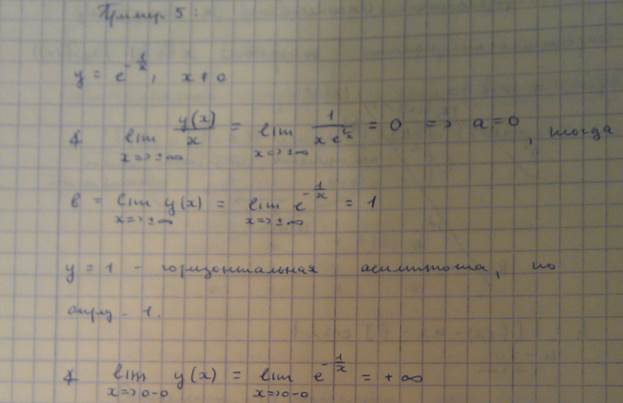
БИЛЕТ 59.
Построение графиков с помощью дифференциального исчесления:локально выпуклые и локально вогнутые функции
Определение: Пусть f(x) определена на X. Функция f(x) называется выпуклой(или выпуклой вниз), если для любого x1 и x2 из промежутка X, выполняется
Функция называется вогнутой(или выпуклой вверх), если f(g1x1+g2x2)>=g1f(x1)+g2f(x2).
Сформулируем определение выпуклой или вогнутой функции основанное на понятии дифференциирования.
Определение: Пусть f(x) имеет в точке С f’(x) говорят, что функция f(x) локально выпуклая(т.е. локально выпуклая вниз) в точке С, если существует такая окрестность точки С, O=(c-E;c+E),
что в любой точке х из О, кривая y=f(x) лежит над касательной к кривой y=f(x) в точке С
И аналогично говорят что f(x) локально вогнута(т.е. локально выпукла вверх) если при любом х из О, кривая y=f(x) лежит под касательной к кривой y=f(x) в точке С.
Т.е. пусть функция y=f(x) имеет в точке С f’’(x) => если f’’(c)>0 (<0), то тогда f(x) является локально
Выпуклой(локально вогнутой) в точке С.
Доказательство:
Справа от точки С график лежит выше положительной.
Определение: если функция y=f(x) является локально выпуклой(локально вогнутой) в любой х из Х, то говорят что f(x) выпуклая(вогнутая) на промежутке Х
|
|
|
