 |
Классическое определение вероятности
|
|
|
|
Модуль 3.
Лекция 18
Раздел 18.2.Определения вероятности
Вероятностное пространство Случай конечного или счетного числа исходов. Отступление. Немного о комбинаторике
Классическое определение вероятности
Статистическое определение вероятности
Геометрические вероятности
Приложение. Из истории теории вероятностей. Парадокс де Мере
Вопросы для самоконтроля
- Каково классическое определение вероятности события?
- Что такое статистическое определение вероятности?
- Что такое геометрическое определение вероятности?
- С чем связана необходимость введения различных определений понятия «вероятность события»?
5. Кубик подбрасывается 10 раз. Найти вероятность того, что все разы выпадало одинаковое количество очков.
6. Между двумя игроками проводится n партий, причем каждая партия кончается или выигрышем, или проигрышем, и всевозможные исходы партий равновероятны. Найти вероятность того, что определённый игрок выиграет ровно m партий, 0 £ m £ n.
7. В студенческой группе 15 человек, из них 10 юношей и 5 девушек. Разыгрываются 3 билета на концерт. Какова вероятность того, что среди выигравших будет одна девушка и двое юношей?
8. В круг вписан квадрат. Наудачу в круг бросается точка. Какова вероятность того, что она попадет в квадрат
9. Иванов и Петров договорились встретиться в кафе в обеденный перерыв с 13 до 14 часов. Иванов имеет возможность ждать друга в течение 20 минут, а Петров – 5 минут. Время прихода каждого в течение часа случайно. Найти вероятность того, что друзья все-таки встретятся.
Литература к разделу 18.2.
А.Н. Кричивец, Е.В. Шикин, А.Г.Дьячков «Математика для психологов» Часть III, пп.1-2
|
|
|
А.Н.Бородин Элементарный курс теории вероятностей и математической статистики» Часть I, пп.2-7
А.В.Дорофеева «Высшая математика. Гуманитарные специальности» Глава 13, пп. 13.2-13.5
Б.В.Гнеденко «Курс теории вероятностей» глава 1
Г.Секкей «Парадоксы теории вероятностей», Гл.1
В.Феллер «Введение в теорию вероятностей и ее применение» т.1, Ведение, глава I
«В свое время, когда я только-только начинал размышлять о вероятности, все казалось мне простым и ясным, и лишь теперь я постигаю глубину своего заблуждения. Всякий раз, как мне кажется, что я нашел истину, она ускользает из моих рук. Почти на каждом шагу подстерегают нас здесь ловушки…» ( из письма Блеза Паскаля Пьеру Ферма от 8 ноября 1654 г.)
Вероятностное пространство Случай конечного или счетного числа исходов.
Отступление. Напомним основные положения комбинаторики-
– раздела дискретной математики, отвечающего на вопрос, сколькими способами можно выполнить некоторое действие. Они понадобятся нам для определения числа исходов, образующих событие (благоприятствующих ему) и использования в решении задач классического определения вероятности
Комбинаторные формулы и правила
При решении задач комбинаторики используют следующие правила.
Правило суммы. Если некоторый объект А может быть выбран из множества объектов m способами, а другой объект В может быть выбран n способами, то выбрать либо А, либо В можно m + n способами.
Правило произведения. Если объект А можно выбрать из множества объектов m способами и после каждого такого выбора объект В можно выбрать n способами, то пара объектов (А, В) в указанном порядке может быть выбрана m · n способами.
Замечание. Набор (множество) элементов, для которых важен порядок следования, называется упорядоченным.
Правило (Принцип) Дирихле. Если вы хотите распределить n объектов по m (условным) ящикам, причем m строго меньше, m<n, то найдется по крайней мере один ящик, в котором будет находиться больше одно объекта
|
|
|
Замечание. Иногда можно встретить этот принцип под названием «принцип голубей» (рассаживание голубей по клеткам, в переводной литературе) или принцип кроликов (рассаживание кроликов по ящикам, в отечественной)
Определение. Множество (набор элементов) называется упорядоченным, если в нем важен порядок следования элементов. В противном случае множество называется неупорядоченным. Примером упорядоченных множеств могут служить номера телефонов, порядок лекций в расписании, набор цифр при последовательном наборе кода замка. Неупорядоченных – набор цифр кода при одновременном наборе цифр, множество членов семьи и пр.
Определения.
Пусть имеется множество, состоящее из n элементов. Обозначим его U n. Перестановкой из n элементов называется заданный упорядоченный набор всех элементов множества U n.
Примеры перестановок:
1)распределение n различных должностей среди n человек;
2)расположение n различных предметов в одном ряду.
Сколько различных перестановок можно образовать во множествеU n? Число перестановок обозначается Pn (читается Р из n).
Чтобы вывести формулу числа перестановок, вспомним правило произведения и представим себе n ячеек, пронумерованных числами 
1,2,... n. Все перестановки будем образовывать, располагая элементы U n в этих ячейках. В первую ячейку можно занести любой из n элементов (иначе: первую ячейку можно заполнить n различными способами). Заполнив первую ячейку, можно n -1 способом заполнить вторую ячейку (иначе: при каждом способе заполнения первой ячейки находится n -1 способов заполнения второй ячейки). Таким образом существует n (n -1) способов заполнения двух первых ячеек. При заполнении первых двух ячеек можно найти n -2 способов заполнения третьей ячейки, откуда получается, что три ячейки можно заполнить n (n -1)(n -2) способами. Продолжая этот процесс, получим, что число способов заполнения n ячеек равно 
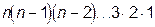. Отсюда
Pn = n (n - 1)(n - 2)...×3×2×1
Число n (n - 1)(n - 2)...×3×2×1, то есть произведение всех натуральных чисел от 1 до n, называется факториалом (читается " n -факториал") и обозначается n!. Отсюда Pn = n!
|
|
|
Пример. Сколькими способами можно поставить в шеренгу 5 человек? 
.
Замечание. По соглашению считается: 1!=1; 0!=1.
Размещениями из n элементов по k элементов будем называть упорядоченные подмножества, состоящие из k элементов, множества Un -(множества, состоящего из n элементов). Число размещений из n элементов по k элементов обозначается 
(читается " А из n по k ").
Примеры задач, приводящих к необходимости подсчета
1) Сколькими способами можно выбрать из 15 человек 5 кандидатов и назначить их на 5 различных должностей?
2) Сколькими способами можно из 20 книг отобрать 12 и расставить их в ряд на полке?
Для подсчета используем тот же метод, что использовался для подсчета Pn,только здесь возьмем лишь k ячеек. Первую ячейку можно заполнить n способами, вторую, при заполненной первой, можно заполнить n -1 способами. Можно продолжать этот процесс до заполнения последней k -й ячейки. Эту ячейку при заполненных первых k -1 ячейках можно заполнить n -(k -1) способами (или n - k +1). Таким образом, все k ячеек заполняются числом способов, равным
Отсюда получаем: 
Пример. Сколько существует различных вариантов выбора 4-х кандидатур из 9-ти специалистов для поездки в 4 различных страны?
Замечание. При этом, если немного изменить условие на выбор 4 специалистов в состав одной делегации, то подмножество станет неупорядоченным, порядок следования специалистов неважен (не привязан к странам), важно лишь наличие того или иного человека в группе.
Замечание. В задачах о размещениях полагается k < n. В случае, если k = n, легко получить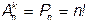 
То есть перестановку из n элементов можно назвать размещением из n элементов по n.
Сочетаниями из n элементов по k элементов называются подмножества, состоящие из k элементов множества Un (множества, состоящего из n элементов).
Одно сочетание от другого отличается только составом выбранных элементов (но не порядком их расположения, как у размещений).
Число сочетаний из n элементов по k элементов обозначается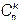 
(читается " C из n по k ").
Замечание. Очевидно, что число сочетаний из n элементов по k элементов меньше числа размещений n элементов по k элементов в k! (число перестановок из k элементов) раз
|
|
|
Примеры задач, приводящих к необходимости подсчета числа сочетаний:
1) Сколькими способами можно из 15 человек выбрать 6 кандидатов для назначения на работу в одинаковых должностях?
2) Сколькими способами можно из 20 книг отобрать 12 книг?
Выведем формулу для подсчета числа сочетаний. Пусть имеется множество Un и нужно образовать упорядоченное подмножество множества Un, содержащее k элементов (то есть образовать размещение). Делаем это так:
1) выделим какие-либо k элементов из n элементов множества Un Это, согласно сказанному выше, можно сделать 
способами;
2) упорядочим выделенные k элементов, что можно сделать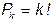 
способами. Всего можно получить 
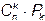вариантов (упорядоченных подмножеств), откуда следует: 
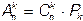,то есть
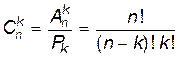
Пример: 6 человек из 15 можно выбрать числом способов, равным
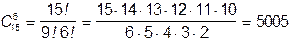
Замечание. В англоязычной литературе (и в некоторых отечественных учебниках) принято другое обозначение для числа сочетаний из n по k: 
Задачи на подсчет числа подмножеств конечного множества называются комбинаторными. Рассмотрим некоторые комбинаторные задачи.
1.Из семи заводов организация должна выбрать три для размещения трех различных заказов. Сколькими способами можно разместить заказы?
Так как все заводы различны, и из условия ясно, что каждый завод может либо получить один заказ, либо не получить ни одного, здесь нужно считать число размещений
2.Если из текста задачи 1 убрать условие различия трех заказов, сохранив все остальные условия, получим другую задачу. Теперь способ размещения заказов определяется только выбором тройки заводов, так как все эти заводы получат одинаковые заказы, и число вариантов определяется как число сочетаний.
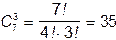
3.Имеются 7 заводов. Сколькими способами организация может разместить на них три различных производственных заказа? (Заказ нельзя дробить, то есть распределять его на несколько заводов).
В отличие от условия первой задачи, здесь организация может отдать все три заказа первому заводу или, например, отдать два заказа второму заводу, а один - седьмому.
Задача решается так. Первый заказ может быть размещен семью различными способами (на первом заводе, на втором и т.д.). Разместив первый заказ, имеем семь вариантов размещения второго (иначе, каждый способ размещения первого заказа может сопровождаться семью способами размещения второго). Таким образом, существует 7×7=49 способов размещения первых двух заказов. Разместив их каким-либо образом, можем найти 7 вариантов размещения третьего (иначе, каждый способ размещения первых двух заказов может сопровождаться семью различными способами распределения третьего заказа). Следовательно, существуют 49×7=73 способов размещения трех заказов. (Если бы заказов было n, то получилось бы 7 n способов размещения).
|
|
|
4.Как решать задачу 3, если в ее тексте вместо слов "различных производственных заказа" поставить "одинаковых производственных заказа"?
5.Добавим к условию задачи 1 одну фразу: организация также должна распределить три различных заказа на изготовление деревянных перекрытий среди 4-х лесопилок. Сколькими способами могут быть распределены все заказы?
Каждый из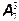 
способов распределения заказов на заводах может сопровождаться 
способами размещения заказов на лесопилках. Общее число возможных способов размещения всех заказов будет равно
Классическое определение вероятности
Вероятность события характеризует возможность (шанс) осуществления события в ходе случайного эксперимента. Смысл вероятности раскрывается в следующих требованиях, налагаемых на вероятности событий. Вероятность события выражается долей от целого, то есть является числом от нуля до единицы. При этом за единицу принимается вероятность наступления достоверного события, то есть события, которое обязательно происходит в ходе эксперимента. Вероятности невозможных событий считаются равными нулю. Если взять произвольный конечный или счетный набор событий, таких, что никакие два из них не могут произойти одновременно, то вероятность наступления хотя бы одного из этих событий должна быть равна сумме вероятностей этих событий. Иначе говоря,
Каждому элементарному исходу wi пространства W соответствует некоторая неотрицательная числовая характеристика Pi шансов его появления, называемая вероятностью исхода w i , причем
(здесь суммирование ведется по всем i, для которых выполняется условие: w i ÎW).
Отсюда следует, что 0 £ Pi £ 1для всех i.
Определение 18.2.1.Вероятность события А (классическое определение) определяется как сумма вероятностей всех элементарных исходов, благоприятствующих событию А. Обозначим ее Р (А).
(*)
Рассмотрим простейшую модель теории вероятностей, которую часто называют «классической схемой». Если каждый элементарный исход имеет одинаковую возможность осуществиться (то есть они равновозможны), то этим исходам логично было бы поставить в соответствие одинаковые вероятности. Если вероятности всех n исходов равны р, а в силу нормировки np=1, то p = 1/n ( где n – число исходов эксперимента ). Исходы (элементарные события), составляющие данное событие А, напомним, называются благоприятствующими событию А. и в случае, когда все исходы равновозможны, вероятность события А Р(А) есть отношение числа m благоприятствующих событию А (обозначается # А = m) исходов из Ω к общему числу n исходов(множеству точек W, # Ω = n), P(A) = m/n. Это и есть классическое определение вероятности
Примеры таких случайных экспериментов: подбрасывание симметричной монеты, бросание правильной игральной кости, случайное извлечение игральной карты из перетасованной колоды.
Из вышесказанного видно, что
1) 0 £ P (A) £ 1;
2) P (W)=1;
3) P (Æ)=0.
(Æ - невозможное событие, то есть событие, не имеющее в своем составе исходов, пустое множество)
Замечание 18.2.1.. Из того, что вероятность выпадения, скажем, герба при подбрасывании монеты равна ½ не следует, что из каждых двух бросков один будет заканчиваться выпадением герба. Это значит длишь, что если бросать монету достаточно долго, то в среднем гербы выпадут в половине случаев.
Примеры 18.2.1..
1)В урне 10 одинаковых по размерам и весу шаров, из которых 4 красных и 6 голубых. из урны извлекается один шар. Какова вероятность того, что извлеченный шар окажется голубым?
Решение. Событие "извлеченный шар оказался голубым" обозначим буквой А. Данное испытание имеет 10 равновозможных элементарных исходов, из которых 6 благоприятствуют событию А. В соответствии с формулой классического определения
Р(А) = 6/10 = 0,6.
2) Все натуральные числа от 1 до 30 записаны на одинаковых карточках и помещены в урну. После тщательного перемешивания карточек из урны извлекается одна карточка. Какова вероятность того, что число на взятой карточке окажется кратным 5?
Решение. Обозначим через А событие «число на взятой карточке кратно 5». В данном испытании имеется 30 равновозможных элементарных исходов, из которых событию А благоприятствуют 6 исходов (числа 5, 10, 15, 20, 25, 30). Следовательно,
Р(А)= 6/30 = 1/5 = 0,2.
3). Подбрасываются два игральных кубика, подсчитывается сумма очков на верхних гранях. Найти вероятность события В, состоящего в том, что на верхних гранях кубиков в сумме будет 9 очков.
Решение. В этом испытании всего 62 = 36 равновозможных элементарных событий. Событию В благоприятствуют 4 исхода:
(3;6), (4;5), (5;4), (6;3), поэтому
Р(В) = 4/36 = 1/9
4). Подбрасываются две симметричные монеты. Чему равна вероятность того, что на верхних сторонах обеих монет оказались цифры?
Решение. Обозначим буквой D событие "на верхней стороне каждой монеты оказалась цифра". В этом испытании 4 равновозможных элементарных исходов: (Г, Г), (Г, Р), (Р, Г), (Р,Р). (Запись (Г, Р) означает,
что на первой монете герб, на второй – «решетка» (цифра). Событию D благоприятствует один элементарный исход (Р, Р). Поскольку m = 1, n = 4, то P(D)=1/4 =0,25.
5) Из набора, содержащего 10 одинаковых на вид электроламп, среди которых 4 бракованных, случайным образом выбирается 5 ламп. Какова вероятность, что среди выбранных ламп будут 2 бракованные (событие Е)?
Здесь элементарным событием является выбор пяти ламп из 10 возможных. Выбор любой пятерки ламп имеет одну и ту же вероятность.
Очевидно, что порядок следования ламп в пятерке нам неважен, существенно лишь, сколько из них являются работающими, а сколько – бракованными. Поэтому для подсчета мы выбираем подсчет сочетаний, то есть неупорядоченных наборов. Всего существует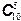 
способов составить такую пятерку, то есть случайный эксперимент в данном случае имеет N = 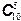равновероятных исходов.
Сколько из этих исходов удовлетворяют условию "в пятерке две бракованные лампы", то есть сколько исходов принадлежат интересующему нас событию?
Каждую интересующую нас пятерку можно составить так: выбрать две бракованные лампы, что можно сделать числом способов, равным 
. Каждая пара бракованных ламп может встретиться столько раз, сколькими способами ее можно дополнить тремя не бракованными лампами, то есть 
раз. Получается, что число пятерок, содержащих две бракованные лампы, согласно правилу произведения, равно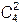 
× .
6). Кодовый замок содержит 10 цифр от 0 до 9. Замок открывается, если одна за другой последовательно нажимаются 3 разных цифры. Некто случайным образом набирает код. Какова вероятность того, что дверь откроется (событие F)?
Здесь элементарным событием будет набор некоторого трехзначного кода, порядок цифр в котором, естественно, важен, поэтому для подсчета мы будем использовать упорядоченные наборы – размещения. Всего различных трехзначных кодов из 10 цифр можно образовать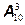 
вариантов и вероятность того, что код угадан (а есть только одна правильная комбинация) составляет
P (F) = 
Ниже следует Приложение, описывающее один из самых известных эпизодов, связанных с историей развития Теории вероятностей. Тех, кто интересуется историей науки мы адресуем, например, к книгам А.Реньи «Письма о вероятности» (М.Мир, 1970) и Г.Секей «Парадоксы теории вероятностей и математической статистики».
Приложение.
|
|
|
