Формула полной вероятности.

Раздел 18.4. Условные вероятности. Независимость событий

Независимые события. Теоремы о сложении и умножении вероятностей

Формула полной вероятности

Формула Байеса

Вопросы для самоконтроля

1. Дайте определение вероятности события А при условии, что произошло событие В
2. Какие события называются независимыми? Дайте 2 варианта определения
3. Сформулируйте теорему о сложении вероятностей
4. Сформулируйте теорему об умножении вероятностей
5. Что такое полная группа событий?
6. Выведите формулу полной вероятности
7. Выведите формулу Байеса
8. Есть четыре кубика с цифрами на гранях 1,2,…,6 и одна правильная пирамида с цифрами на гранях 1,2,3,4. Наугад выбрали предмет и бросили. Выпала цифра 4. Какова вероятность того, что взяли кубик?
9. Есть 10 симметричных монет, 8 нормальных, а на двух – на обеих сторонах герб. Наудачу взятая монета бросается 3 раза. Найти вероятность того, что выпадут три герба

 

Литература

А.Н. Кричивец, Е.В. Шикин, А.Г.Дьячков «Математика для психологов» Часть III, пп.1-2

А.Н.Бородин Элементарный курс теории вероятностей и математической статистики» Часть I, пп.1-7

А.В.Дорофеева «Высшая математика. Гуманитарные специальности» Глава 13, пп. 13.1-13.5

Б.В.Гнеденко «Курс теории вероятностей» глава 1

Г.Секкей «Парадоксы теории вероятностей», Гл.1

В.Феллер «Введение в теорию вероятностей и ее применение» т.1, Ведение, глава I

 

Формулы сложения вероятностей.

Из пункта 2 приведенной аксиомы следует, что если A ₁ и A₂ несовместные события, то

P (A ₁U A ₂) = P (A ₁) + P (A ₂)

Если A ₁ и A ₂ — совместные события, то A ₁U A ₂ =(A ₁\ A ₂)U A ₂, причем очевидно, что A ₁\ A ₂ и A ₂ — несовместные события. Отсюда следует:

P (A ₁U A ₂) = P (A₁\ A ₂) + P (A₂) (*)

Далее очевидно: A₁ = (A₁\ A ₂)U(A ₁∩ A ₂), причем A₁\ A ₂ и A ₁∩ A ₂- несовместные события, откуда следует: P (A ₁) = P (A₁\ A ₂) + P (A ₁∩ A ₂) Найдем из этой формулы выражение для P (A₁\ A ₂) и подставим его в правую часть формулы (*). В результате получим формулу сложения вероятностей:

P (A ₁U A ₂) = P (A ₁) + P (A ₂) – P (A ₁∩ A ₂)

Из последней формулы легко получить формулу сложения вероятностей для несовместных событий, положив A ₁∩ A ₂= Æ.

Пример 18.4.1. Спортсмен стреляет по мишени, разделенной на 3 сектора.

Вероятность попадания в первый сектор равна 0,4, во второй - 0,3.

Какова вероятность попадания либо в первый, либо во второй сектор?

Решение. События А " попадание в первый сектор" и В - "попадание во второй сектор" несовместны (попадание в один сектор исключает попадание во второй), поэтому применима теорема сложения вероятностей несовместных событий. В соответствии с этой теоремой находим искомую вероятность:

Р(А + В) = Р(А) + Р(В) = 0,4 + 0,3 = 0,7.

 

Пример 18.4.2. Найти вероятность вытащить даму или пиковую масть при случайном отборе одной карты из колоды в 32 листа.

Р (дама) = 4/32 = 1/8; Р (пиковая масть) = 8/32 = 1/4;

Р (пиковая дама) = 1/32;

Р ((дама) U (пиковая масть)) = 1/8 + 1/4 - 1/32 =11/32

Тот же результат можно получить, пересчитав число благоприятных исходов с помощью классического определения вероятности

 

Пример 18.4.3. Вероятность попадания в мишень для первого спортсмена

0,85, а для второго - 0,8. Спортсмены независимо друг от друга

сделали по одному выстрелу. Найти вероятность того, что в мишень

попадет хотя бы один спортсмен?

Решение. Введем обозначения: события А. - "попадание первого

спортсмена", В - "попадание второго спортсмена", С - "попадание хотя

бы одного из спортсменов". Очевидно, А + В = С, причем события А и В

совместны. В соответствии с общей формулой сложения вероятностей получаем

Р(С) = Р(А) + Р(В) - Р(АВ), а поскольку А и В независимы

Р(С) = Р(А)+ Р(В)-Р(А)Р(В),

Подставив данные значения Р(А) = 0,85, Р(В) = 0,8 в формулу

для Р(С), найдем искомую вероятность Р(С) = (0,85 + 0,8) - 0,85·0,8 = 0,97.

 

 

Условные вероятности.

Рассмотрим задачу. Студент перед экзаменом выучил из 30 билетов билеты с номерами с 1 по 5 и с 26 по 30. Известно, что студент на экзамене вытащил билет с номером, не превышающим 20. Какова вероятность, что студент вытащил выученный билет?

Определим пространство элементарных исходов: W={1,2,3,...,28,29,30}. Пусть событие А заключается в том, чтостудент вытащил выученный билет: А = {1,...,5,25,...,30,}, а событие В — в том, что студент вытащил билет из первых двадцати: В = {1,2,3,...,20}

Событие А ∩ В состоит из пяти исходов: (1,2,3,4,5), и его вероятность равна 5/30. Это число можно представить как произведение дробей 5/20 и 20/30. Число 20/30 - это вероятность события B. Число 5/20 можно рассматривать как вероятность события А при условии, что событие В произошло (обозначим её Р (А / В); другой вариант обозначения Р(А|В)). Таким образом решение задачи определяется формулой

P (А ∩ В) = Р (А / В) Р (B)

Эта формула называется формулой умножения вероятностей, а вероятность Р (А / В) — условной вероятностью события A.

 

Итак, определение 18.4.1.. Вероятность события А, при условии, что произошло событие В, называется условной вероятностью и обозначается Р(А|В).

Определим условные вероятности Р(А|В) для схемы, когда все исходы равновозможны. Событие В произошло, поэтому мы можем рассматривать только те исходы, которые составляют В. Соответственно, у нас образуется новое пространство элементарных событий Ω*, совпадающее с событием (множеством) В. Нас интересуют те исходы, которые входят и в А и в В, и образуют область А ∩ В. Теперь рассмотрим условную вероятность А|В с точки зрения классического определения.

Р(А|В) равна отношению числа исходов в области А∩В к общему числу исходов в новом пространстве элементарных событий Ω*, то есть отношению

 

Р(А | В) =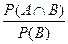

 

Замечание 18.4.1.. Таким образом, условная вероятность – это «обычная» вероятность, но определенная на суженном пространстве элементарных событий. В силу этого для нее сохраняются все свойства ранее определенной вероятности.

 

Замечание 18.4.2.. Отсюда следует теорема Умножения вероятностей, согласно которой Р(А∩В) = Р(А|В) × Р(В)

 

Пример.18.4.1 Из шляпы, в которой сидят 7 белых и 3 черных кроликов, наудачу один за другим извлекают (без возвращения) двух кроликов. Какова вероятность того, что первый зверь будет белым, а второй черным?

Пусть X — событие, состоящее в извлечении первым белого кролика, а Y — событие, состоящее в извлечении вторым черного кролика. Тогда X ∩ Y - событие, заключающееся в том, что первый кролик будет белым, а второй — черным. P (Y / X) =3/9 =1/3 — условная вероятность извлечения вторым черного кролика, если первым был извлечен белый (после излечения первым белого кролика в шляпе осталось 9 кроликов – новое Ω*, из которых белых – теперь 6, а черных по-прежнему 3).Учитывая, что P (X) = 7/10, по формуле умножения вероятностей получаем: P (X ∩ Y) = 7/30

Определение 18.4.2. События А и В называются независимыми, если Р (А / В)= Р (А). Иначе говоря, то, что событие В имело место никак не повлияло на вероятность события А

Замечание 18.4.3. За определение независимых событий можно принять следствие последней формулы и формулы умножения

P (А ∩ В) = Р (А) Р (B)

Пример 18.4.2. Рассмотрим задачу, аналогичную предыдущей, но с одним дополнительным условием: вытащив первого кролика, запоминаем его цвет и возвращаем зверя в шляпу, после чего даем кроликам поперемещаться. В данном случае результат второго извлечения никак не зависит от того, какой кролик - черный или белый появился при первом извлечении. Вероятность появления первым белого кролика (событие А) равна 7/10. Вероятность события В - появления вторым черного кроля - равна 3/10. Теперь формула умножения вероятностей дает: P (А ∩ В) = 21/100.

Извлечение шаров (кроликов) способом, описанным в этом примере, называется выборкой с возвращением или возвратной выборкой.

 

Замечание 18.4.3. (о связи между совместными и зависимыми событиями). Между понятиями „ несовместные " и „ независимые " события имеется следующая связь:

1) если А и В — несовместные события (и Р(А) ≠0, и P(В) ≠ 0), то они обязательно зависимые;

2) если А и В — совместные события, то они могут быть и зависимыми, и независимыми;

3) если А и В — зависимые события, то они могут быть и совместными, и несовместными.

 

Замечание 18.4.4.. Понятие независимости является очень важным в теории вероятностей. При этом следует различать формальное понятие независимости событий, определяемое свойствами вероятностной модели, и понятие независимости событий, возникающее в прикладных задачах и означающее, что события не связаны причинно. При корректном построении вероятностной модели второе трансформируется в первое, но это может быть не всегда.

 

Замечание 18.4.5. Следует помнить, что при использовании теоремы сложения вероятностей нужно проверять несовместность событий, а при использовании теоремы умножения независимость событий.

 

Пусть пространство элементарных событий W разбивается на непересекающиеся события (события, не имеющие общих исходов), их вероятности можно вычислить. Кроме того, можно вычислить условную вероятность некоторых событий, при условии, что произошло событие из указанной группы. В этом случае оказывается удобным использовать формулу полной вероятности и следующую из нее формулу Байеса.

 

Замечании 18.4.6. Нижеследующий раздел имеет непосредственное отношение к психологии. Как мы принимаем решения, руководствуясь опытом, как по известному факту установить, что он был вызван именно этой причиной и пр., а также увлекательная история открытия Байеса изложены в блестящей книге Леонарда Млодинова «(Не)совершенная случайность», с которой мы очень рекомендуем Вам познакомиться.

Формула полной вероятности.

Определение 18.4.3. Группа событий H ₁, H ₂,..., H_n называется полной группой событий, если выполняются следующие условия:

1) Все события попарно несовместны: H_i ∩ H_j =; i, j =1,2,..., n; ij

2) Их объединение образует пространство элементарных событий W:

W =H ₁U H ₂U... U H_n.

Рис.1

Замечание. Обозначения H ₁, H ₂,..., H_n отсылают к статистике, где они обозначают гипотезы (от английского Hypothesis)

 

 

Пусть А - некоторое событие: А Ì W (рис.1). Тогда имеет место формула полной вероятности:

P (A) = P (A / H ₁) P (H ₁) + P (A / H ₂) P (H ₂) +...+ P (A / H_n) P (H_n) =

Доказательство. Очевидно: A = (A ∩ H ₁) U (A ∩ H ₂) U...U (A ∩ H_n), причем все события A ∩ H_i (i = 1,2,..., n) попарно несовместны. Отсюда по теореме сложения вероятностей получаем

P (A) = P (A ∩ H ₁) + P (A ∩ H ₁) +...+ P (A ∩ H_n)

Если учесть, что по теореме умножения P (A ∩ H _i) = P (A/H_i) P (H _i),

(i = 1,2,..., n), то из последней формулы легко получить приведенную выше формулу полной вероятности.

 

Пример 18.4.4. На книжном складе находятся учебники, напечатанные в трех типографиях, причем доля первой типографии - 30, второй - 50, третьей - 20. Брак в их продукции составляет соответственно 0,5, 0,3 и 0,2. Какова вероятность того, что случайно полученный на складе учебник оказалась бракованным?

Пусть событие H ₁ состоит в том, что выбранный учебник напечатан в первой типографии, H ₂ ч – на второй и H ₃,соответственно на третьей. чевидно:

P (H ₁) = 3/10, P (H ₂) = 5/10, P (H ₃) = 2/10.

Пусть событие А состоит в том, что выбранный учебник оказался бракованным; A/H_i означает событие, состоящее в том, что выбран бракованный учебник из книг, напечатанных в i -й типографии. Из условия задачи следует:

P (A/H ₁) = 5/1000; P (A/H ₂) = 3/1000; P (A/H ₃) = 2/1000

По формуле полной вероятности получаем

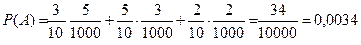
Формула Байеса

Пусть H ₁, H ₂,..., H_n - полная группа событий и А ÌW - некоторое событие. Тогда по формуле для условной вероятности

Здесь P (H_k | A) - условная вероятность события (гипотезы) H_k или вероятность того, что H_k реализуется при условии, что событие А произошло.

По теореме умножения вероятностей числитель формулы можно представить в виде

P (H_k ∩ A) = P (A ∩ H_k) = P (A | H_k) P (H_k)

Для представления знаменателя формулы можно использовать формулу полной вероятности

P (A)

Определение 18.4.5. Теперь можно получить формулу, называемую формулой Байеса:

Замечание 18.4.7. По формуле Байеса исчисляется вероятность реализации гипотезы H_k при условии, что событие А произошло. Формулу Байеса еще называют формулой вероятности гипотез.

Замечание 18.4.8. Вероятности P(H_k) (k=I,2,..., n) событий H₁,H₂,...,H_n

до опыта называются априорными вероятностями (от латинского a priori, что означает "сперва", Т.е. в данном случае до того, как был произведен опыт). ' Вероятности P(H_k) (k = 1,2,..., n) тех же событий называются апостериорными (от латинского слова а posteriori, что означает "после", Т.е. в данном случае после опыта).

Пример 18.4.5. Рассмотрим приведенную выше задачу об учебниках, только изменим вопрос задачи. Пусть библиотекарь получил на складе учебник, и он оказался бракованным. Найти вероятность того, что этот учебник был напечатан во второй типографии.

Выпишем формулу Байеса для этого случая

Из этой формулы получаем: P (H ₂ / A) = 15/34

.

 

 

Поделиться:

Воспользуйтесь поиском по сайту: