Последовательный алгоритм компоновки и списковые страницы данных

Будем описывать схему с помощью ГГ:

,

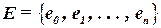Задача: требуется разбить схему на блоки 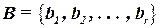так, чтобы каждый блок содержал не более чем заданные число элементов 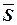и число внешних выводов .

В рассматриваемом алгоритме процесс формирования очередного блока начинается с выбора первого, так называемого базового элемента (БЭ). В качестве БЭ выбирается элемент, имеющий максимальное число общих цепей со всеми еще нераспределенными элементами (элемент e₀ уже распределен). далее блок последовательно заполняется элементами из числа еще нераспределенных. Для этого из множества всех нераспределенных элементов выделяется подмножество таких элементов, распределение которых в блок не приводит к превышению заданного числа выводов из блока. Из них в блок распределяется элемент, имеющий максимальное число общих цепей со всеми элементами, уже распределенными в блок. Если таких элементов несколько, то среди них выбирается элемент, при добавлении которого в блок число выводов из блока минимально. Если и таких элементов несколько, то выбирается элемент с максимальным порядковым номером (для формализации задачи).

Рассмотрим более подробно процедуру формирования блока b_j. Будем считать, что блоки b₁, b₂, …, b_j-1 уже сформированы. Пусть I_j – множество элементов, нераспределенных в эти предшествующие блоки, т. е.

,

где E(b_k) – множество элементов блока b_k.

Последовательный алгоритм компоновки можно представить в следующем виде.

П. 1.

При выборе БЭ для всех элементов вычисляется оценка L₁(x).

,

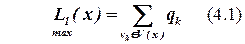Здесь q_k – связи элемента со всеми нераспределенными элементами,

V(x) – множество цепей, инцидентных элементу x,

E(v_k) – множество элементов, инцидентных цепи v_k,

L₁(x) – число связей элемента x со всеми еще неразмещенными элементами.

В блок распределяется элемент с максимальной оценкой L₁(x). Если таких элементов несколько, то выбирается элемент с большим порядковым номером (для формализации задачи).

П. 2.

Пусть на t -м шаге формирования блока b_j имеется множество элементов 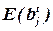, распределенных к этому шагу в блок b_j (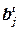). При определении очередного элемента для всех нераспределенных элементов вычисляется оценка L₂(x).

,

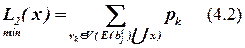Здесь 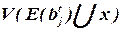– множество цепей, инцидентных всем элементам блока b_j к шагу t, включая элемент x,

L₂(x) – число выводов блока b_j на шаге t с учетом элемента x.

П. 3.

Для всех элементов x, для которых выполняется условие 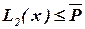, вычисляется оценка L₃(x) – число связей элемента x с формируемым блоком .

,

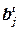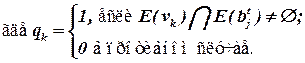
В блок b_j включается элемент с максимальной оценкой L₃(x). Если таких элементов несколько, то среди них выбирается элемент с минимальной оценкой L₂(x). Если и таких элементов несколько, то выбирается элемент с максимальным порядковым номером (для формализации задачи).

П.4. Если ни для одного элемента условие 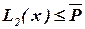не выполняется, то дополнение блока b_j прекращается и начинается формирование следующего блока (переход к п.1).

П. 5. Алгоритм заканчивает работу когда все элементы схемы распределены в блоки.

При практической реализации алгоритма вместо формулы (4.2) для определения числа выводов из блока удобно использовать формулы для приращения числа выводов из блока b_j при добавлении в него элемента x.

,

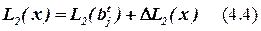где 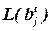– количество выводов блока b_j до добавления в него элемента x.

,

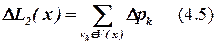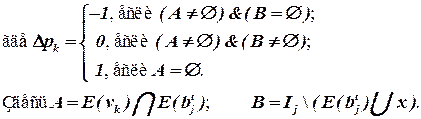
Последнее выражение (для ∆ p_k) можно пояснить с помощью рисунка 4.1.

14.Алгоритм Рабина.

Увеличение быстродействия в алгоритме Рабина достигается за счёт преимущественного распространения волны в направлении ячейки-цели.

В алгоритме Ли, который является реализацией метода динамического программирования, такая целенаправленность при поиске трассы отсутствует.

Алгоритм Рабина, который реализует метод ветвей и границ, позволяет также, как и алгоритм Ли, находить глобальный оптимум целевой функции.

Пусть требуется найти путь минимальной длины между ячейками А и В.

Рассмотрим некоторую ячейку С_i, включаемую в очередной фронт волны. Значение волновой функции P_i, приписываемое С_i ячейки фронта, определяется из выражения:

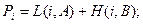(1), где L(i,A) – длина пройденного волной пути из ячейки А в ячейку С_i, а

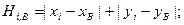- расстояние между ячейками С_i,В и В в ортогональной метрике.

Нетрудно видеть, что 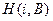является нижней оценкой пути из С_i в В, полученной в предположении отсутствия препятствий на этом пути. Отсюда выражение (1) в целом представляет собой нижнюю оценку пути из А в В, проходящую через ячейку С_i.

Согласно методу ветвей и границ, оптимальное решение следует искать в подмножестве решений, имеющем наилучшую оценку.

Согласно методу ветвей и границ, оптимальное решение следует искать в подмножестве решений, имеющем наилучшую оценку. В соответствии с этим в сформированном очередном фронте волны выделяют подмножество ячеек с min оценкой 1 и распространение волны на следующем шаге осуществляется из ячеек этого подмножества.

Заметим, что для сокращения зоны поиска, распространение волны в алгоритме Рабина осуществляется в первую очередь, из тех ячеек с min оценкой, которые получили эту оценку последними.

Последовательность просмотра соседних ячеек та же, что и в алгоритме Ли (например:,,,) – построение пути осуществляется с использованием путевых координат.

Эффективность алгоритма Рабина по сравнению с алгоритмом Ли показана на рис. 1, на котором для каждой ячейки ДПР указано значение весовой функции P_i. Цифрами в правых углах ячеек обозначена последовательность просмотра ячеек на этапе распространения волны стрелками указаны путевые координаты ячеек.

 

Рисунок 1.

Примечание. Волна распространяется от ячейки с минимальным значением весовой функции и большим порядковым номером. В данном примере рассмотрено всего45ячеек ДРП вместо84ячеек обычного алгоритма Ли.

 

 

⇐ Предыдущая234567891011Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: