Непрерывных случайных величин.

Так как непрерывная случайная величина может принимать любые значения в некотором интервале, то невозможно перечислить все значения случайной величины и указать их вероятности как для дискретных величин. Для количественной характеристики распределения непрерывных случайных величин служат две основные статистические функции: функция плотности распределения вероятностей f(x) и функция распределения вероятностей (или накопленной вероятности) F(х).

Значений непрерывной величины может быть бесчисленное множество, поэтому вероятность отдельного значения равна 0. Практической мерой вероятности данного значения х служит вероятность того, что случайная величина примет значение, лежащее в каком–либо интервале Dх, например, от х=a до х+Dх=b. Плотностью распределения вероятностей называется отношение вероятности Р(a<x<b) попадания случайной величины x в тот или иной интервал Dx ее значений к величине этого интервала: . Зависимость плотности распределения от значений величины x: y=f(x) называется функцией плотности распределения вероятностей (рис.3).

Рис.3. График функции плотности распределения

вероятностей непрерывной случайной величины.

Вероятность Р(a<x<b) попадания значений случайной величины x в интервал между значениями a и b определится как площадь кривой между ординатами x=а и x=b. Эта площадь равна определенному интегралу от функции y=f(x) в этих пределах:

Р(a<x<b) = = F(x) =F(b) – F(a)(7)

Функция F(х) – является первообразной для у=f(х ) и называется функцией распределения вероятностей (или накопленной вероятности).

В общем случае эта функция равна вероятности того, что случайная величина Х меньше наперед заданного числа x.

F(x) = P(Х<x) (8)

При любом значении x функция распределения равно сумме вероятностей всех значений Х, меньших x. Как и всякая вероятность, функция распределения не может быть отрицательной и больше единицы 0 (рис.4).

Рис.4. Примерный график функции распределения

непрерывной случайной величины.

 

Вероятность попадания случайной величины на отрезок (а, в) равна приращению функции распределения на этом отрезке:

Р(a<x<b)=F(b) – F(a) (9)

 

Условие X<x можно записать в виде двойного неравенства:

- <X<x, тогда выражение (7) примет вид:

Р(- <X<x)= = F(x) (10)

Если промежуток изменения случайной величины от - до + , то попадание в такой интервал является достоверным событием и его вероятность равна 1.

= 1 (11)

Это соотношение называется условием нормировки функции плотности распределения вероятностей. Для непрерывной случайной величины с плотностью распределения y = f(x) математическое ожидание М(x) и дисперсия D(x) вычисляется по следующим формулам:

М(x)= , D(x)= (12)

На практике выполняют построение приближенного графика функции плотности распределения вероятностей случайной величины – гистограммы. Для этого промежуток возможных значений случайной величины разделяется на ряд равных интервалов: Dx₁=x₁¸x₂; Dx₂=x₂¸x₃;...; Dx_n=x_n-1¸x_n и определяется частота (m_i) появления тех или иных значений данной величины в этих интервалах (классах). Например, изучается распределение студентов на 1 курсе по возрасту. Полученные значения распределили по 5 интервалам с Dx_i =3:

возраст по годам [15–18) [18–21) [21–24) [24–27) [27–30)

число студентов 9 48 25 10 8

Значения абсолютных или относительных частот в соответствующем масштабе откладываются на графике в виде площадей прямоугольников, построенных на отрезках Dx₁ , Dx₂ ,... Dx_n, как на основаниях.

Возраст

 

Рис.5. Гистограмма распределения студентов по возрасту.

 

Кривая, соединяющая середины прямоугольников, называется полигоном распределения. Так как при достаточно большом числе n случаев, относительная частота появления тех или иных значений случайной величины x соответствует их вероятности Р(x), то можно считать, что площади прямоугольников, составляющих гистограмму, пропорциональны вероятностям попадания случайной величины в соответствующий интервал Dx. Высота прямоугольников будет являться плотностью распределения вероятностей. Функция плотности распределения вероятностей f(х) в этом случае имеет ступенчатый характер. При достаточно большом числе интервалов на гистограмме функция распределения вероятностей приобретает плавный характер (пунктирная линия на рис.5). В пределе, при Dx 0 построенное нами распределение дискретной случайной величины стремится к распределению непрерывной случайной величины. Таким образом, распределение непрерывной случайной величины можно приближенно заменить распределением дискретной случайной величины.

Для ряда непрерывных случайных величин, сгруппированных в классы, математическое ожидание и дисперсия вычисляются по формулам (3), (5), где m – число попаданий в класс, n – общее количество величин, <x_i> – средняя величина в классе. В нашем примере:

Таблица 3

№ класса	Величина интервала	<xi>	mi	Pi=mi/n	<xi>Pi	(<xi>-M)2	(<xi>-M)2 Pi
	[15–18)	16,5		0,09	1,485	23,04	2,0736
	[18–21)	19,5		0,48	9,36	3,24	1,5552
	[21–24)	22,5		0,25	5,625	1,44	0,36
	[24–27)	25,5		0,1	2,55	17,64	1,764
	[27–30)	28,5		0,08	2,28	51,84	4,1472

å=100 М(x)=21,3 D(x)=9,9

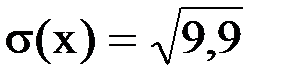=3,15

На практике ряд распределения (вариационный ряд) составляют следующим образом:

1. Из имеющихся значений признака x выбирают наименьшее (x_min)_, наибольшее (x_max), определяют размах распределения

(x_max – x_min).

2. Определяют число классов группировки. Для определения числа классов можно воспользоваться формулой: k=1+3,32·lg n, где n – число измерений. Величину k округляют до целых чисел.

3. Определяют оптимальную величину класса (интервала группировки) Dx_i= . Эту величину также можно округлять соответственно точности значений x.

4. Выбирают границы классов. Границы первого класса следует выбрать так, чтобы он содержал наименьшее значение, но не начинался с него, например, класс может начинаться с величины (x_min – 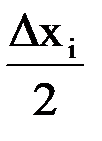). Последующие классы образуются добавлением величины интервала Dx_i. Если нижняя граница класса совпадает с верхней границей предыдущего класса, это значение следует отнести к данному классу. Например, [1–2), [2–3) и т.д.

5. Определяют середину интервала <x_i>.

Задание: Для ряда измерений роста студентов сгруппировать данные по классам, определить математическое ожидание, дисперсию и среднее квадратическое отклонение. Построить гистограмму и полигон распределения.

148 158 150 162 170 156 186 151 161 152 171 165 174 157 172 172 177 166 157 149 159 154 164 167 173 176 147 163 185 164 161 153 168 162 184 162 169 154 167 163 166 172 158 155 165 179 165 160 159 169

Нормальный закон распределения случайных величин.

 

Для того чтобы обрабатывать результаты экспериментов, важно знать, к какому виду распределения случайных величин относятся полученные результаты. Например, в физике распределение скоростей молекул газа при тепловом движении подчиняется распределению Максвелла. Распределение дискретных случайных величин может подчиняться биномиальному закону, для редких событий справедливо распределение Пуассона и т.д. Важное место в статистике вообще и в биологической статистике в частности, занимает нормальное распределение (распределение Гаусса). Нормальное распределение возникает тогда, когда на изменение случайной величины действует множество различных независимых факторов, каждый из которых в отдельности не имеет преобладающего значения. Многие распределения биологических признаков, характеризующиеся непрерывной вариацией, а также ошибки измерений подчиняются нормальному закону.

Размещение вариант при нормальном распределении характеризуется определенными закономерностями:

Параметр m характеризует математическое ожидание (среднее арифметическое) случайной величины, являясь центром распределения и наиболее вероятным значением. Изменение математического ожидания не влияет на форму кривой, а только вызывает ее смещение вдоль оси x.

Параметр s характеризует изменчивость случайной величины (меру растянутости кривой вдоль оси x): чем больше s, тем больше кривая растянута.

График нормальной кривой симметричен относительно прямой x=m (одинаковые по абсолютной величине отрицательные и положительные отклонения случайной величины от центра равновероятны).

По мере увеличения разности (x–m) значение f(x) убывает. Это значит, что большие отклонения менее вероятны, чем малые. При (x–m) 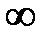значение f(x) стремится к нулю, но никогда его не достигает.

График функции нормального распределения представляет собой колоколообразную кривую (рис.6).

Рис.6. Кривая нормального распределения.

 

Для нормального распределения, имеющего математическое ожидание mи среднее квадратическое отклонение s, плотность распределения вероятности имеет вид:

f(x) = , (13)

а функция распределения вероятности равна:

(14)

Для перехода от двух параметров распределения mи s к одному, делают замену переменной:

t= , dx= s dt, (15)

с помощью которой функцию (14) можно привести к виду:

(16)

Функция (16) не выражается через элементарные функции, но для нее составлены таблицы, которые называются таблицами нормального интеграла вероятности. Вероятность того, что значение случайной величины попадет в интервал от а до b:

Р(a<x<b)= (17)

при этом значения функции Ф находят по таблице 1 Приложения. Для нее выполняется соотношение: Ф(–t) = 1– Ф(t).

В нашем примере распределения студентов по возрасту, функция распределения будет иметь вид:

F(x)= 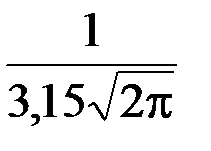dx (18)

Найдем вероятность того, что на первый курс поступят вундеркинды в возрасте младше 16 лет:

P(x<16)= =Ф(–1,6825)=1–0,9535=0,0465=4,65%.

Задание: Анализ веса 75 новорожденных детей показал, что у них в интервал от 1 до 1,9 кг попало 5 новорожденных, 2 – 2,9 кг – 25 новорожденных, 3 – 3,9 кг – 40 новорожденных, 4 – 4,9кг – 5 новорожденных. Записать функции плотности вероятности f(x) и распределения вероятностей F(x) для предполагаемого нормального распределения веса новорожденных, определить вероятность рождения недоношенного ребенка весом <2,5 кг.

Функция нормального закона распределения, как правило, симметрична относительно математического ожидания. Если же варианты накапливаются преимущественно в правой или левой части ряда, то говорят об асимметрии. Мерой скошенности ряда служит коэффициент асимметрии А. Для симметричных кривых распределения А равен нулю, для правоасимметричных А>0, для левоасимметричных А<0. Асимметрия считается незначительной, если А 0,2. При А 0,5 скошенность кривой считается сильной (рис.7а). Показатель эксцесса (Е) характеризует вершину кривой распределения.

А= ; E= – 3 (19)

Для распределений с резко выраженным пиком (островершинных)

Е >0, для плосковершинных Е <0 (рис 7б).

Рис.7а. Рис.7б.

 

Если число измерений в некоторых классах мало, или исследуемый материал не является однородным, можно наблюдать многовершинные распределения.

 

Интервальные оценки.

 

Для изучения закономерностей вариации при нормальном распределении широко пользуются величиной нормированного отклонения t. Мы ввели этот параметр в уравнении (15) для преобразования переменных при вычислении функции распределения вероятностей. Смысл такого преобразования (нормирования) заключается в том, что за начало отсчета значений случайной величины берется математическое ожидание (среднее значение), а среднее квадратическое отклонение используется как единица измерения. Нормированное отклонение представляет собой отклонение той или иной варианты от математического ожидания,выраженное в сигмах:

t= , отсюда х – μ=σt. (20)

Каждая варианта характеризуется определенным значением t, указывающим ее положение в ряду значений или на кривой распределения. Так, если какая то варианта имеет значение t=1,5, это значит, что она располагается в правой части кривой на расстоянии в 1,5σ. Если варианта имеет значение t=-2,5, то она расположена в левой части кривой на расстоянии от μ в 2,5σ и т.д. Зная вариационную кривую распределения вариант по тому или иному признаку и предполагая, что распределение является нормальным, можно заранее предсказать, какой процент изученных вариант укладывается в пределах 1σ, в пределах 2σ, в пределах 3σ. Так, в пределах 1σ – располагается 68,3% всего ряда, в пределах 2σ – 95,5% и в пределах 3σ – 99,7% всех вариант.

Вероятности 0,95 и 0,99 (95% и 99%), получили название доверительных вероятностей, т.е. таких, значениям которых можно достаточно доверять или которыми можно уверенно пользоваться. Доверительные вероятности, в свою очередь, определяют доверительные границы или доверительный интервал, в котором может находиться случайная величина. Из уравнения (20) можно записать выражение для интервала значений случайной величины х:

Δх=±st. (21)

Произведение st будет определять величину интервала, в котором может находиться случайная величина с заданной степенью вероятности. Вероятность любого отклонения от средней, как функция нормированного отклонения, определяется с помощью таблицы 2 Приложения. Геометрически величины, находящиеся в таблице, являются долями площади нормальной кривой в границах от -t до +t, выражающие в то же время и вероятность. Первая колонка слева таблицы 2 дает значения t с одним десятичным знаком, второй десятичный знак t представлен 10 столбцами, на которых вверху стоят цифры от 0 до 9. Тогда t=1,00 соответствует вероятность 0,6827 (11–я строка, 1–я цифра) и т.д. В то же время, задаваясь определенным уровнем вероятности, можно определить t. Для различных вероятностей доверительные интервалы будут следующими:

Вероятности Интервалы

0,95 ±1,96s

0,99 2,58s

0,999 3,03s

Определенным значениям вероятностей соответствуют так называемые уровни значимости. По отношению к закономерностям нормального закона распределения, уровень значимости обозначает вероятность выхода случайной величины за пределы доверительного интервала. Если доверительную вероятность обозначить – Р, а уровень значимости – a, то a=1 – Р. Для доверительной вероятности 0,95 – уровень значимости будет равен 0,05 (5% вариант могут выйти за пределы доверительного интервала), для доверительной вероятности 0,99, a=0,01 и т.д. В медико–биологических исследованиях используются как доверительные вероятности (Р), так и уровни значимости(a).

Рис.8. Нормальная кривая с доверительным интервалом при Р=0,95

Рассчитаем, какая доля вариант находится в вариационной кривой между -1,5s и +1,0s пользуясь таблицей 2 Приложения. В интервале между -1,5s и +1,5s находится 0,8664 всех вариант. Следовательно, в интервале между -1,5s и 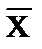: (0,8664:2)=0,4332. Аналогично, в интервале 1,0s – 0,6827 всех вариант. От до +1,0s находится 0,6827:2=0,3414. Следовательно, в интервале от -1,5s до +1,0s находится 0,4332+0,3414=0,7746 вариант (77,46%).

Задание: Рассчитайте, какая доля вариант находится в вариационной кривой между -1s и 2,8s, между и +2,6s, между и -1,8s, в интервале 0,68s, за пределами +2,2s.

Ответы: 0,839, 0,495, 0,46, 0,50, 0,0139.

 

⇐ Предыдущая12345678Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: