 |
Рассмотрим применение понятий матрицы и определителя к решению систем линейных уравнений.
|
|
|
|
 Системой линейных уравнений будем называть непустое конечное множество линейных уравнений. В общем случае система линейных уравнений относительно неизвестных х1, х2,...,хn имеет вид:
Системой линейных уравнений будем называть непустое конечное множество линейных уравнений. В общем случае система линейных уравнений относительно неизвестных х1, х2,...,хn имеет вид:
a11 x1 + a12 x2 + … + a1n xn = b1
a21 x1 + a22 x2 + … + a2n xn = b2 (1)
................................................................................
am1 x1 + am2 x2 + … + amn xn = bm
Здесь предполагается, что aij, bi – заданные действительные числа. Числа aij называются коэффициентами при неизвестных системы, bi - свободными членами.
Решением системы (1) называется такая упорядоченная совокупность п элементов поля Р (с1 с2,..., сп), которая при подстановке в систему (1) на место неизвестных (х1, х2,…, хп) обращает все уравнения этой системы в тождества.
Система (1), имеющая по крайней мере одно решение, называется совместной, не имеющая решений - несовместной. Если система (1) имеет только одно решение, она называется определенной, если более одного решения - неопределенной.
Элементарными преобразованиями системы (1) называются следующие два преобразования:
1) умножение обеих частей одного из уравнений на любой отличный от нуля элемент поля Р;
2) i-ое уравнение заменяется уравнением
(ai1 + cak1)xl +...+(ain + cakn)xn = bi + cbk, где с- некоторый элемент поля Р.
Система, полученная из системы (1) с помощью элементарных преобразований, имеет те же решения, что и система (1). Пользуясь элементарными преобразованиями и, в случае необходимости, заменой обозначений  переменных, можно привести систему (1) к следующему виду:
переменных, можно привести систему (1) к следующему виду:

 (2)
(2)
где r≤ п; bii¹0, i=1, 2,..., r, или обнаружить, что она несовместна.
Если r=п, т. е. последнее уравнение имеет вид bnnxn=bn, bпп¹0, то система (2), а значит, и система (1) имеют единственное решение. Если r<n, то произвольное решение системы (2) можно найти следующим образом: неизвестным хr+1, хr+2,..., хп придаются произвольные числовые значения, а значения остальных неизвестных находятся последовательно из уравнений системы (2). Такой способ решения системы (1) называется методом Гаусса.
|
|
|
 Пример 2. Решить систему линейных уравнений методом Гаусса
Пример 2. Решить систему линейных уравнений методом Гаусса
Для упрощения записи решения составим матрицу из коэффициентов системы линейных уравнений. Решение этой системы оформляем следующим образом:





При приведении произвольной системы линейных уравнений к ступенчатому виду, над уравнениями системы мы производили следующие преобразования, которые называют элементарными преобразованиями:
а) умножение обеих частей одного уравнения на действительное число, не равное нулю;
б) прибавление к обеим частям одного уравнения соответствующих частей другого, умноженных на любое число.
При этом следует отметить, что каждому элементарному преобразованию, производимому над системой линейных уравнений, соответствует преобразование над строками матрицы системы. Эти преобразования над матрицами будем называть элементарными.
Линейные системы очень часто встречаются в математике, и так называемые линейные методы, конечным результатом которых часто являются решения линейных систем, составляют ее наиболее развитую часть. Кроме того, решение большого числа практических задач на ЭВМ также сводится к линейным системам.
Отмечаем, что упомянутый выше метод является типичным математическим алгоритмом, приспособленным для решения массовых задач.
Рассмотрим систему n линейных алгебраических уравнений относительно n неизвестных х1, х2,...,хn:
 a11 x1 + a12 x2 + … + a1n xn = b1
a11 x1 + a12 x2 + … + a1n xn = b1
a21 x1 + a22 x2 + … + a2n xn = b2
................................................................................
an1 x1 + an2 x2 + … + ann xn = bn
Эта система в «свернутом» виде может быть записана в виде
 , i = 1, 2,..., n.
, i = 1, 2,..., n.
В соответствии с правилом умножения матриц, рассмотренная система линейных уравнений может быть записана в матричном виде:
|
|
|

 АХ =В, где
АХ =В, где

А=, Х=, В=
Матрица А, столбцами которой являются коэффициенты при соответствующих неизвестных, а строками – коэффициенты при неизвестных в соответствующем уравнении, называется матрицей системы; матрица – столбец В, элементами которой являются правые части уравнений системы, называется матрицей правой части или просто правой частью системы. Матрица – столбец Х, элементы которой – искомые неизвестные, называется решением системы.
Таким образом, система линейных алгебраических уравнений может быть записана в виде простейшего матричного уравнения АХ = В.
Если матрица системы невырождена (определитель её отличен от нуля), то у нее существует обратная матрица и тогда решение системы легко получить, умножив обе части уравнения АХ =В cлева на матрицу А-1: А-1 (АХ) = А-1В, а поскольку А-1А = Е и ЕХ = Х, то Х = А-1В.
Пример 4. Решить систему линейных уравнений в матричном виде:

 Запишем данную систему линейных уравнений в матричной форме:
Запишем данную систему линейных уравнений в матричной форме:
 ×
×  =
= 
Найдем А-1 =  .
.
Тогда Х = А-1В =  ·
·  =
=  .
.
Ответ: {(-1, 11, -28)}.
Рассмотрим еще один способ решения систем линейных уравнений, называемый правилом Крамера.
Теорема 4. Пусть имеется система n линейных алгебраических уравнений относительно n неизвестных х1, х2,..., хn:
 a11 x1 + a12 x2 + … + a1n xn = b1
a11 x1 + a12 x2 + … + a1n xn = b1
a21 x1 + a22 x2 + … + a2n xn = b2
................................................................................
an1 x1 + an2 x2 + … + ann xn = bn
Если определитель основной матрицы не равен нулю, то система уравнений имеет единственное решение, которое находится по формулам: x1 =  , x2 =
, x2 =  ,… xn =
,… xn =  , где
, где  i получается из матрицы А заменой i –того столбца столбцом свободных членов.
i получается из матрицы А заменой i –того столбца столбцом свободных членов.
Пример 5. Решить систему уравнений по правилу Крамера:

В виде матрицы эту систему можно записать таким образом: A=  , где свободные члены уравнений будут находится в последнем столбце и отделены вертикальной чертой. Теперь мы введем понятие основного определителя; в данном случае он будет выглядеть таким образом:
, где свободные члены уравнений будут находится в последнем столбце и отделены вертикальной чертой. Теперь мы введем понятие основного определителя; в данном случае он будет выглядеть таким образом:
 =
=  =-25. Основным определителем является матрица, составленная из коэффициентов стоящих при переменных.
=-25. Основным определителем является матрица, составленная из коэффициентов стоящих при переменных.
 1 =
1 = 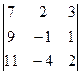 =-75,
=-75,  2 =
2 =  = 25,
= 25,
 3 =
3 =  =50.
=50.
Воспользуемся следующими формулами:
x1 =  =3, x2 =
=3, x2 =  =-1, x3 =
=-1, x3 =  =2.
=2.
|
|
|


