 |
Характеристики магнитного поля. Принцип суперпозиции полей
|
|
|
|
КРАТКАЯ ТЕОРИЯ И ОБРАЗЦЫ РЕШЕНИЙ НЕКОТОРЫХ ЗАДАЧ
М А Г Н И Т Н О Е П О Л Е
ХАРАКТЕРИСТИКИ МАГНИТНОГО ПОЛЯ. ПРИНЦИП СУПЕРПОЗИЦИИ ПОЛЕЙ
Экспериментальные факты свидетельствуют, что при движении электрических зарядов наряду с электрическим полем возникает новый вид силового поля – магнитное поле. Магнитное поле в вакууме в любой момент времени характеризуется вектором магнитной индукции В (r,t), который является аналогом вектора напряженности электрического поля. В качестве пробного объекта в случае магнитного поля используется рамка с током. Магнитная индукция как силовая характеристика поля может быть определена отношением максимального вращающего момента, действующего на рамку с током, к величине ее магнитного момента
(3.1.1)
Магнитный момент рамки (витка) с током
Р m = I S n, (3.1.2)
где I – сила тока, текущего по рамке; S - ее площадь; n – единичный орт по нормали к плоскости рамки. Таким образом, магнитный момент – это векторная величина, направленная по нормали к рамке. Положительное направление нормали и направление тока в рамке составляют правовинтовую систему.
Закон, определяющий вектор магнитной индукции точечного заряда, движущегося со скоростью v = const, (v<< с, где с = 3 · 108 м/ с – скорость света в вакууме), выглядит следующим образом:
(3.1.3)
где μо = 4π ·10-7 Гн / м (генри /метр) – магнитная постоянная; r – радиус – вектор, проведенный от заряда q к точке наблюдения (рис.1).
Направление магнитной индукции удобно находить, пользуясь мнемоническим правилом правого винта: если поступательное движение совпадает с направлением движения положительного заряда или тока в проводнике, то направление вращения указывает ход силовых линий магнитного поля (они всегда замкнуты). Для нахождения вектора магнитной индукции надо провести касательную к силовой линии в нужной точке (рис. 1, силовая линия изображена пунктиром).
|
|
|
 |  | ||
Рис.1 Рис.2
В международной системе единиц СИ единицей магнитной индукции является тесла (Тл). Наряду с вектором В используется вектор напряженности магнитного поля Н. Вектора В и Н связаны выражением
В = μ0 μ Н, (3.1.4)
где μ - относительная магнитная проницаемость среды. Единица измерения напряженности магнитного поля в СИ – ампер на метр (А/м).
Величину магнитной индукции поля, созданного элементом проводника (рис. 2), определяют по закону Био – Савара – Лапласа:
или в скалярной форме:
, (3.1.5)
где r – радиус – вектор, проведенный от элемента тока Id l к точке, в которой определяют магнитную индукцию; α - угол между элементом dl и радиусом – вектором r.
Принцип суперпозиции говорит о том, что магнитная индукция результирующего поля, созданного несколькими объектами (токами или движущимися зарядами), равна векторной сумме магнитных индукцией полей, создаваемых каждым объектом в отдельности:
или 
(3.1.6)
Из формул (1.1.6) и (1.1.5) можно вывести формулы для расчета магнитной индукции в некоторых частных случаях: для поля прямого и кругового токов.
Магнитная индукция поля отрезка прямого проводника с током (рис. 3) в точке А
(3.1.7)
где α1 – угол между элементом тока Id l и радиусом – вектором r, проведенным в точку А из начала проводника (откуда ток вытекает); 
- то же, но радиус – вектора проводится в точку А из конца проводника (куда течет ток).
Пример. Найти магнитную индукцию поля, созданного бесконечно длинным проводником, согнутым под прямым углом, в точке А, лежащей на биссектрисе угла на расстоянии а = 6 см от вершины угла (рис.4). По проводнику течет ток 1 А.
|
|
|
 | |||
 | |||
Рис.3 Рис.4
Решение. Проводник можно представить в виде двух полубесконечных проводников. Для вертикального проводника угол α1 = 0 (стремится к этому значению при условии, что верхний конец провода уходит в бесконечность); α2 = 1350 (в вершине угла С элемент тока Id l направлен вниз, а радиус – вектор – к точке А). Для горизонтального проводника α1- 45о, α2 стремится к 180о, так как элемент тока Id l в конце проводника направлен вправо, а радиус – вектор – к точке А.
Воспользуемся принципом суперпозиции (3.1.6). С учетом того, что магнитная индукция от той и другой части провода направлена к нам (силовые линии показаны пунктиром), из формулы (3.1.7) запишем выражение для индукции результирующего поля
В = 
[ (cos 0o – cos 135o) + (cos 45o – cos 180o)] = = 
(1 + √ 2/2 
+ √ 2/ 2 + 1) = 
= 
Тл = 8,1 мкТл,
где b = а √ 2 – кратчайшее расстояние от точки А до поводника.
Ответ: В = 8,1 мкТл.
Для бесконечно длинного проводника расстояния от обоих концов проводника до точки А значительно больше, чем кратчайшее расстояние от проводника до нее (α1 = 0о ; α2 = 180о), и формула (3.1.7) принимает вид:
В =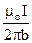 
. (3.1.8)
Магнитная индукция поля кругового витка с током в точке А, лежащей на оси витка, перпендикулярной его плоскости (рис. 5),
В = 
, (3.1.9)
где R –радиус витка, x- расстояние от плоскости витка до точки.
Если взять точку в центре кругового тока, то x = 0, и формула принимает вид:
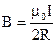, (3.1.10)
Пример. Определить магнитную индукцию в точке А поля, созданного круговым витком с током I =2 А и прямым бесконечно длинным проводником с током I = 1 А (рис. 6). Радиус витка R = 5 см, расстояние b = 10 см. проводник расположен перпендикулярно к плоскости рисунка, ток течет от нас (общепринятое обозначение «от нас» Ä, Á к нам).
 | |||
 |
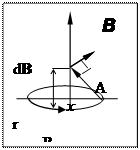Рис.5. Рис.6.
Решение. В точке А поле создается двумя проводниками. Сначала определим значения магнитной индукции для отдельных проводников по формулам (3.1.10) и (3.1.8). Учитывая направления векторов, определяемые по правилу правого винта, и принцип суперпозиции, можно записать для магнитной индукции результирующего поля:
|
|
|
В = 
.
Тогда
В = 
= 
.
Подставляя числовые данные задачи, получим:
В = 23,14 · 10-7 
= 25мкТл.
Ответ: В = 25 мкТл.
|
|
|
