 |
Вопрос 38. Интеграл от функции комплексной переменной. Его свойства. Вычисление
|
|
|
|
Вопрос 35. Дифференцирование функций комплексной переменной. Условие Коши-Римана.
Пусть функция w = f (z) определена в некоторой области G комплексной плоскости. Пусть точки z и z +D z принадлежат области G. Положим D w = f (z +D z)– f (z), D z = D x + i D y.
Функция w=f (z) называется дифференцируемой в точке zОG,если существует предел 
Этот предел называют производной функции f (z) и обозначают через f¢ (z) (или 
).
Итак,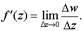 
Пусть z=x+iy, w=f (z) =u (x,y) +iv (x,y), тогда в каждой точке дифференцируемости функции f (z) выполняются соотношения:
Эти соотношения принято называть условиями Коши-Римана (или уравнениями Коши-Римана). Когда в некоторой точке (x,y) выполняются условия Коши-Римана и, кроме того, функции u (x,y) и v (x,y)дифференцируемы как функции действительных переменных, то функция f (z) =u+iv дифференцируема в точке z = x + iy как функция комплексного переменного z.
Вопрос 36. Понятие аналитической функции. Ее свойства. Условие гармоничности
Функция f(z) 
C(g), дифференцируемая (моногенная) во всех точках z g, производная которой f ' (z) C(g) называется аналитической функцией в области g.
Обозначение: f(z) C 
(g).
Понятие аналитичности функции определяет глобальное поведение f(z) в области g.
Свойства аналитических функций.
1) Если f(z) C (g) (аналитическая в g), то f(z) C(g) (непрерывна в g).
2) Сумма и произведение аналитических функций есть аналитическая функция. Частное аналитических функций есть аналитическая функция всюду, где знаменатель отличен от нуля.
3) Если w=f(z) C (g) - аналитическая функция комплексной переменной z, причем в области ее значений G на плоскости w определена аналитическая функция
x=j (w) C (G), то функция F(z)= j [f(z)] C (g) -аналитическая функция комплексной переменной z в области g.
4) Пусть w=f(z)=u(x,y)+iv(x,y) C (g) и f '(z0) 
0, z0 g. Тогда в окрестности точки w0=f(z0) определена обратная аналитическая функция z=j (w) C (|w-w0|<e) отображающая эту окрестность на окрестность точки z0, причем j'(w0)=1/ f '(z0).
|
|
|
5) Пусть в односвязной области g плоскости (x,y) задана функция u(x,y), являющаяся действительной частью аналитической функции f(z). Тогда мнимая часть этой функции определяется с точностью до аддитивной постоянной.
Условие Гармоничности: Дифференцируя первое соотношение Коши-Римана 
по переменной х, второе соотношение 
по переменной у, получим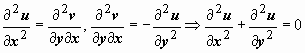 
, т.е. Δ u = 0 (Δ - оператор Лапласа), т.е. u (x, y) - гармоническая функция. Дифференцируя первое соотношение Коши-Римана по переменной у, второе соотношение по переменной х, получим 
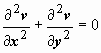, т.е. Δ v = 0, т.е. v (x, y) - тоже гармоническая функция. Пара гармонических функций, связанных соотношениями Коши-Римана, называется сопряжёнными функциями.
Вопрос 37. Восстановление аналитической функции комплексной переменной по ее действительной (мнимой) части.
План решения
1. Находим частные производные заданной функции u(x,y) (или v(x,y)).
2. Используя условия Коши — Римана
находим v(x,y) (или u(x,y)) с точностью до произвольной постоянной C.
3. Записываем искомую функцию f(z) = u(x,y)+iv(x,y)+C и преобразуем полученное выражение к функции переменной z, например, заменяя x и y их выражениями через переменную z:
4. Находим значение постоянной C, используя значение. Записываем ответ.
Вопрос 38. Интеграл от функции комплексной переменной. Его свойства. Вычисление
Определение. Пусть на комплексной плоскости С задана ориентированная кусочно-гладкая кривая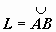 
, на которой определена функция w = f (z). Разобьём кривую точками z 0 = A, z 1, z 2, …, zn = B на n частей, на каждой из дуг 
выберем произвольную точку tk, найдём f (tk) и составим интегральную сумму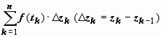 
. Предел последовательности этих сумм при n → ∞,max|Δ z k | → 0 (k = 1, 2,..., n), если он существует, не зависит ни от способа разбиения кривой на дуги, ни от выбора точек tk, называется интегралом от функции w = f (z) по кривой L и обозначается 
.
Теорема. Если функция w = f (z) непрерывна на кривой L, то она интегрируема по этой кривой.
|
|
|
Свойства интеграла от ФКП. Мы доказали, что 
выражается через два действительных криволинейных интеграла второго рода, поэтому он обладает всеми свойствами этих интегралов:
1. 
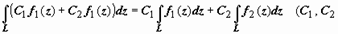- произвольные комплексные постоянные);
2. 
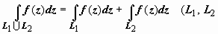- кривые без общих внутренних точек):
3. 
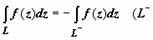- кривая, совпадающая с L, но проходимая в противоположном направлении;
4. Если l - длина кривой L, | f (z)| ≤ M при z ∈ L, то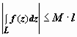 
.
5) Вычисление интеграла интегрированием по параметру: 
f(z)dz=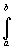 
f[z(t)] z '(t)dt.
6) Замена переменных. Пусть $ j (x): z=j (x); C<=> G на плоскости x и j (x)О C (D) и однолистная в D, где D- область комплексной плоскости x, содержащая G.
=> f(z)dz= 
f[j (x)]j '(x)dx.
|
|
|
