Алгоритм Берленкемпа-Месси.

Пусть P – некоторое поле, e – единица поля P. Обозначим через начальный отрезок произвольной последовательности u элементов поля P. Будем говорить, что многочлен

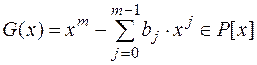
вырабатывает отрезок , если

,

то есть данный отрезок последовательности является отрезком некоторой линейной рекуррентной последовательности с характеристическим многочленом G (x). Алгоритм Берленкемпа-Месси строит многочлен G (x) наименьшей степени, вырабатывающий отрезок .

Определим функцию умножения последовательности на многочлен. Для произвольного многочлена и последовательности v положим H (x) · v = w, где

Многочлен G (x) вырабатывает l ³ m знаков последовательности u, если выполняется равенство

то есть если первые l – m знаков последовательности v равны нулю, а следующий за ними отличен от нуля.

Для многочлена G (x) Î P [ x ] степени m и последовательности u введем параметры l_u (G) и k_u (G) = l_u (G) – m Î N È {0, +¥}, где l_u (G) – число знаков последовательности u, вырабатываемых многочленом G (x). Ясно, что k_u (G) – максимальное число первых подряд идущих нулей в последовательности G (x) · u (либо ¥).

Будем индуктивно строить последовательность многочленов G ₀(x), G ₁(x), … неубывающих степеней 0 = m ₀ < m ₁ £ m ₂ £ ….

Начальные условия: G ₀(x) = e, m ₀ = 0.

Этап 1. Если

то полагаем

Если G ₁(x)· u = 0, то есть если k_u (G ₁) = ¥, то G ₁(x) – искомый минимальный многочлен ЛРП u. В противном случае строим G ₂(x).

Этап t + 1. пусть многочлены G ₀(x), …, G_t (x) уже построены, и степень многочлена G_j (x) равна m_j, причем 0 = m ₀ < m ₁ £ m ₂ £ … m_t. Пусть выполняются соотношения

Определим число s = s (t) так, чтобы выполнялись условия m_t = m_t - 1 = … = m_s + 1 > m_s (такое s найдется, так как m ₁ > m ₀). Положим

Если G_{t +1}(x)· u = 0, то нужный многочлен построен. В противном случае строим G_{t +2}(x).

Теорема: Если u – линейная рекуррентная последовательность над полем P с минимальным многочленом степени m, то F (x) = G_t (x) для некоторого подходящего значения t £ 2 m – 1 – k ₀.

Усложнение линейных рекуррентных последовательностей.

Не смотря на достаточно большой период и хорошие статистические качества, линейные рекуррентные последовательности имеют простое строение (ярко выраженная аналитическая связь между предыдущими и последующим элементами последовательности). Поэтому в криптографических приложениях используют различные способы усложнения аналитического строения линейных рекуррент.

Основной подход, применяемый при проектировании генератора гаммы на базе РСЛОС прост. Сначала берется один или несколько РСЛОС, обычно с различными длинами и различными характеристическими многочленами. (Если длины взаимно просты, а все многочлены обратной связи примитивны, то у сконструированного генератора будет максимальный период). Ключ является начальным состоянием регистров. Выходной бит представляет собой функцию, желательно нелинейную, некоторых битов РСЛОС.

Если выходной бит является функцией единственного РСЛОС, то генератор называется фильтрующим генератором.

Рис.22. Фильтрующий генератор.

Если выходной бит является функцией нескольких РСЛОС, то генератор называется комбинирующим генератором.

Рис.23. Комбинирующий генератор.

Еще один тип генераторов представляет собой композицию РСЛОС. В данной схеме выход одного из регистров подается на вход другого регистра.

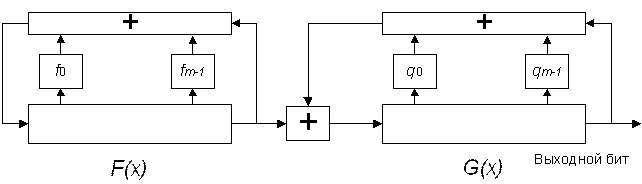
Рис.24. Генератор на основе композиции регистров сдвига..

Кроме перечисленных схем усложнения применяются и другие схемы (с динамическим изменением закона рекурсии с элементами памяти и пр.).

⇐ Предыдущая45678910111213Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: