 |
Проверка статистической значимости выборочного коэффициента корреляции.
|
|
|
|
Модуль 4
Лекция 26
Элементы корреляционного анализа
Понятие функциональной и статистической зависимости
Линейная зависимость. Задачи корреляционного анализа.
Идея метода
Проверка статистической значимости выборочного коэффициента корреляции
Программные положения
Корреляционный анализ – один из методов, связанных с установлением факта существования функциональных ил иных зависимостей, которые могут быть и случайными. Задачи корреляционного анализа – задачи исследования взаимосвязей между отдельными группами переменных, относящихся к группе статистических задач независимости
Методические рекомендации
Перед прочтением текста лекции вспомните определения зависимых и независимых случайных величин, корреляции и коэффициентов корреляции.
Обратите внимание о связи выраженности именно линейной зависимости со значениями коэффициента корреляции
В Дополнении приводится выдержка из книги Г.Секей «Парадоксы теории вероятностей и математической статистики»(глава II «Парадоксы статистики», §5. Парадоксы корреляции). Материал этого приложения представляет исторический и практический интерес, но не обязателен для изучения
Вопросы для самоконтроля
- В чем состоит задача корреляционного анализа?
- Чем отличаются функциональная и статистическая зависимости?
- Какая зависимость называется линейной?
- Что такое коэффициент корреляции?
- Как осуществляется анализ коэффициента корреляции?
- Что такое корреляционная матрица и корреляционная плеяда?
- В результате наблюдений получены следующие данные
| x i | ||||||||||
| yi |
Представить схему ответа на вопрос о наличии корреляции между случайными величинами Х и Y при α =0,05
|
|
|
Литература
О.Ю.Ермолаев «Математическая статистика для психологов» Глава 11
А.Н. Кричивец, Е.В. Шикин, А.Г.Дьячков «Математика для психологов» Глава 7, пп. 7.1. – 7.3, глава 8, пп. 8.1, 8.2
А.Д.Наследов «Математические методы психологического исследования», Главы 6, 8, 10
Отступление. О Функциональной и стохастической связи. Из книги Е.С.Вентцель «Теория вероятностей», п.8.5
Понятие «независимости» случайных величин, которым мы пользуемся в теории вероятностей, несколько отличается от обычного понятия «зависимости» величин, которым мы оперируем в математике. Действительно, обычно под «зависимостью» величин подразумевают только один тип зависимости - полную, жесткую, так называемую - функциональную зависимость. Две величины 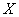 и
и 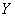 называются функционально зависимыми, если, зная значение одной из них, можно точно указать значение другой.
называются функционально зависимыми, если, зная значение одной из них, можно точно указать значение другой.
В теории вероятностей мы встречаемся с другим, более общим, типом зависимости — с вероятностной или «стохастической» зависимостью. Если величина 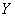 связана с величиной
связана с величиной 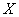 вероятностной зависимостью, то, зная значение
вероятностной зависимостью, то, зная значение 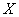 , нельзя указать точно значение
, нельзя указать точно значение 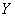 , а можно указать только ее закон распределения, зависящий от того, какое значение приняла величина
, а можно указать только ее закон распределения, зависящий от того, какое значение приняла величина 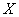 .
.
Вероятностная зависимость может быть более или менее тесной; по мере увеличения тесноты вероятностной зависимости она все более приближается к функциональной. Таким образом, функциональную зависимость можно рассматривать как крайний, предельный случай наиболее тесной вероятностной зависимости. Другой крайний случай - полная независимость случайных величин. Между этими двумя крайними случаями лежат все градации вероятностной зависимости - от самой сильной до самой слабой. Те физические величины, которые на практике мы считаем функционально зависимыми, в действительности связаны весьма тесной вероятностной зависимостью: при заданном значении одной из этих величин другая колеблется в столь узких пределах, что ее практически можно считать вполне определенной. С другой стороны, те величины, которые мы на практике считаем независимыми, и действительности часто находятся в некоторой взаимной зависимости, но эта зависимость настолько слаба, что ею для практических целей можно пренебречь.
|
|
|
Вероятностная зависимость между случайными величинами очень часто встречается на практике. Если случайные величины 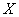 и
и 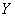 находятся в вероятностной зависимости, это не означает, что с изменением величины
находятся в вероятностной зависимости, это не означает, что с изменением величины 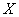 величина
величина 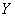 изменяется вполне определенным образом; это лишь означает, что с изменением величины
изменяется вполне определенным образом; это лишь означает, что с изменением величины 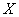 величина
величина 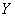 имеет тенденцию также изменяться (например, возрастать или убывать при возрастании
имеет тенденцию также изменяться (например, возрастать или убывать при возрастании 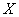 ). Эта тенденция соблюдается лишь «в среднем», в общих чертах, и в каждом отдельном случае от нее возможны отступлении.
). Эта тенденция соблюдается лишь «в среднем», в общих чертах, и в каждом отдельном случае от нее возможны отступлении.
Рассмотрим, например, две такие случайные величины: 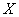 - рост наугад взятого человека,
- рост наугад взятого человека, 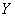 - его вес. Очевидно, величины
- его вес. Очевидно, величины 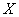 и
и 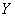 находятся в определенной вероятностной зависимости; она выражается в том, что в общем люди с большим ростом имеют больший вес. Можно даже составить эмпирическую формулу, приближенно заменяющую эту вероятностную зависимость функциональной. Такова, например, общеизвестная формула, приближенно выражающая зависимость между ростом и весом:
находятся в определенной вероятностной зависимости; она выражается в том, что в общем люди с большим ростом имеют больший вес. Можно даже составить эмпирическую формулу, приближенно заменяющую эту вероятностную зависимость функциональной. Такова, например, общеизвестная формула, приближенно выражающая зависимость между ростом и весом:
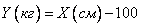 .
.
Формулы подобного типа, очевидно, не являются точными и выражают лишь некоторую среднюю, массовую закономерность, тенденцию, от которой в каждом отдельном случае возможны отступления.
В вышеприведенном примере мы имели дело со случаем явно выраженной зависимости. Рассмотрим теперь такие две случайные величины: 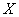 - рост наугад взятого человека;
- рост наугад взятого человека; 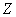 - его возраст. Очевидно, для взрослого человека величины
- его возраст. Очевидно, для взрослого человека величины 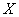 и
и 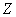 можно считать практически независимыми; напротив, для ребенка величины
можно считать практически независимыми; напротив, для ребенка величины 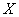 и
и 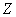 являются зависимыми.
являются зависимыми.
Приведем еще несколько примеров случайных величин, находящихся в различных степенях зависимости.
1. Из камней, составляющих кучу щебня, выбирается наугад один камень. Случайная величина 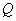 - вес камня; случайная величина
- вес камня; случайная величина 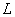 - наибольшая длина камня. Величины
- наибольшая длина камня. Величины 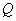 и
и 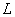 находятся в явно выраженной вероятностной зависимости.
находятся в явно выраженной вероятностной зависимости.
|
|
|
2. Производится стрельба ракетой в заданный район океана. Величина  - продольная ошибка точки попадания (недолет, перелет); случайная величина
- продольная ошибка точки попадания (недолет, перелет); случайная величина 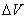 - ошибка в скорости ракеты в конце активного участка движения. Величины
- ошибка в скорости ракеты в конце активного участка движения. Величины  и
и 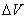 явно зависимы, так как ошибка
явно зависимы, так как ошибка 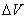 является одной из главных причин, порождающих продольную ошибку
является одной из главных причин, порождающих продольную ошибку  .
.
3. Летательный аппарат, находясь в полете, измеряет высоту над поверхностью Земли с помощью барометрического прибора. Рассматриваются две случайные величины: 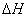 - ошибка измерения высоты и
- ошибка измерения высоты и  - вес топлива, сохранившегося в топливных баках к моменту измерения. Величины
- вес топлива, сохранившегося в топливных баках к моменту измерения. Величины 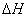 и
и  практически можно считать независимыми.
практически можно считать независимыми.
Напоминание. Зависимость между величинами Х и Y выражаемая формулой Y = f(X) = kX+b где k, b – числовые коэффициенты, называется линейной. Если константа k положительна, зависимость называется прямой, а если отрицательна - то обратной линейной зависимостью.
Зависимая переменная Y может быть случайной величиной, даже если переменные Х1…,Хn не являются случайными, так как значение Y определяется не только значениями переменных (Х1…,Хn), но и неучтенными факторами и ошибками вычислений. Таким образом, связь между (Х1…,Хn) и Y носит не функциональный, а стохастический характер.
И задача корреляционного анализа заключается в исследования наличия взаимосвязи между отдельными группами переменных.
Отступление. Схема «черного ящика («Математическая статистика (т.XVI, МГТУ им.Баумана)
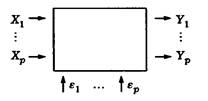 Модель черного ящика – наиболее общая модель любой реальной системы, ассоциированной с по-
Модель черного ящика – наиболее общая модель любой реальной системы, ассоциированной с по-
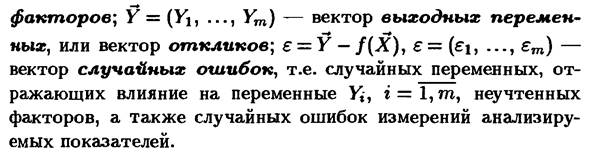
Таким образом, корреляционный анализ – это проверка гипотез о связях между переменными с помощью коэффициентов корреляции
Корреляционный анализ сводится к следующим этапам:
1) Выбор показателя стохастической связи анализируемых переменных – конкретного коэффициента корреляции – количественной меры и направления вероятностной взаимосвязи двух переменных (принимает значение от -1 до +1). К ним относятся коэффициент корреляции Пирсона (обсуждавшийся в теме «Числовые характеристики случайной величины»), коэффициент частной корреляции, ранговые коэффициенты.
|
|
|
2) Вычисление его оценки по имеющимся экспериментальным данным (нахождение соответствующего выборочного коэффициента корреляции)
3) Проверка статистической гипотезы о том, что рассматриваемый коэффициент корреляции значимо отличается от нуля.
Н0: коэффициент корреляции генеральной совокупности = 0.
При отклонении этой гипотезы принимается альтернативная о наличии положительной (у выборочного коэффициента корреляции знак +) или отрицательной (соответственно, −) корреляции. Если по результатам статистической проверки гипотезы о равенстве нулю коэффициента корреляции нулевая гипотеза не отклоняется на уровне значимости α, то делается вывод об обнаружении положительной (или, соответственно) отрицательной связи между Х и Y.
3’) Возможна и другая постановка задачи: сравнение корреляций для двух выборок и проверка основной гипотезы о совпадении коэффициентов корреляции. Тогда возможно два варианта:
1. выборки независимы; необходимо сравнить два коэффициента корреляции, полученных на разных выборках между одними и теми же переменными
2. выборки зависимы: необходимо сравнить корреляцию переменных X и Y с корреляцией переменных Х и Z при условии, что все переменные измерены на одной и той же выборке
Мы рассмотрим только п. 3) в самой простой постановке – проверке гипотезы связи метрических переменных с помощью коэффициента корреляции Пирсона при помощи t-критерия Стьюдента. Относительно п. 3’) заметим, что для решения этой задачи используется Z-критерий.
Замечание 26.1.. Уровень значимости не всегда отражает силу связи. Ниже рассматриваются наиболее частые причины.
Замечание 26.2.. Буквальное значение термина «зависимость» подразумевает влияние, а «связь» - любые согласованные изменения, которые могут объясняться, например, влиянием третьих переменных. Важно иметь в виду, что корреляционные связи не могут рассматриваться как доказательство причинно-следственной зависимости. Они говорят лишь о том, что изменению одного признака сопровождается изменением другого, но не о причине (причинах) согласованности этих изменений.
Замечание 26.3. о коэффициенте корреляции Пирсона. Если произведение
(xi – EX)(yi – EY) положительны, то данные i -го испытуемого свидетельствуют о прямой (положительной) взаимосвязи. То есть, если большинство отклонений положительно, это свидетельствует о прямой пропорциональной связи x и y. Аналогично для преобладающих отрицательных, и сумма произведений отклонений таким образом оказывается показателем направления и силы связи (большая положительная сумма – прямая пропорциональная связь, большая по абсолютной величине, но отрицательная по знаку – обратная; отсутствие связи отражается во взаимном «уравновешивании» положительных и отрицательных произведений и, соответственно, небольшой по абсолютному значению, близкой к нулю, сумме).
|
|
|
Замечание 26.4.. Анализ коэффициентов корреляции может дать информацию о силе связи между переменными. Она достигает максимума, когда имеет место взаимно однозначное соответствие: когда каждому значению первой переменной соответствует ровно одно значение второй (и наоборот). Стохастическая (эмпирическая, экспериментальная) связь при этом совпадает с функциональной линейной зависимостью. Показателем силы связи таким образом является абсолютная (без учета знака) величина коэффициента корреляции
Определение 26.1.. Множество точек, соответствующих экспериментальным данным, называется диаграммой (графиком,областью) двумерного рас с еивания
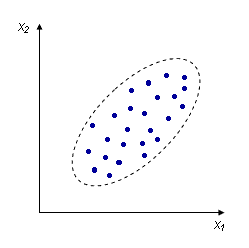

Диаграммы рассеяния, позволяющие предположить наличие прямой и обратной линейной зависимости между величинами Х1 и Х2.
Коэффициент r является случайной величиной, поскольку вычисляется из случайных величин. Для него можно выдвигать и проверять следующие гипотезы:
Проверка статистической значимости выборочного коэффициента корреляции.
Напомним, что проверкой статистической значимости выборочной оценки 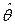 параметра q генеральной совокупности называется проверка статистической гипотезы H 0: q = 0, при конкурирующей гипотезе
параметра q генеральной совокупности называется проверка статистической гипотезы H 0: q = 0, при конкурирующей гипотезе
H 1: q ¹ 0. Если гипотеза H 0 отвергается, то оценка 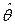 считается статистически значимой.
считается статистически значимой.
Пусть имеются две случайные величины X и Y, определенные на множестве объектов одной и той же генеральной совокупности, причем обе имеют нормальное распределение. Задача заключается в проверке статистической гипотезы об отсутствии корреляционной зависимости между случайными величинами X и Y.
H 0: rXY = 0;
H 1: rXY ¹ 0.
Здесь rXY – коэффициент линейной корреляции.
Производится выборка объема n и вычисляется выборочный коэффициент корреляции r= rXY. За статистический критерий принимается случайная величина
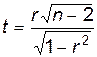 ,
,
которая распределена по закону Стьюдента с n – 2 степенями свободы.
Отметим сначала, что все возможные значения выборочного коэффициента корреляции r лежат в промежутке [–1;1]. Очевидно, что относительно большие отклонения в любую сторону значений t от нуля получаются при относительно больших, то есть близких к 1, значениях модуля r. Близкие к 1 значения модуля r противоречат гипотезе H 0, поэтому здесь естественно рассматривать двустороннюю критическую область для критерия t.
По уровню значимости a и по числу степеней свободы n – 2 находим из таблицы распределения Стьюдента значение t кр. Если модуль выборочного значения критерия t в (выборочное значение статистики критерия) превосходит t кр, то гипотеза H 0 отвергается и выборочный коэффициент корреляции считается статистически значимым. В противном случае, то есть если | t в| < t кр и принимается гипотеза H 0, выборочный коэффициент корреляции считается статистически незначимым.
Пример 26.1.
Пусть в некотором эксперименте коэффициент корреляции между величинами X и Y при числе испытуемых n=7 оказался равным 0,75. Пусть a=0,05. H0: rXY=0 и H1: rXY≠0. Чтобы оценить истинность этой гипотезы на заданном уровне значимости, необходимо сначала найти критическое значениеtкр, зависящее от a и от числа степеней свободы = n-2=5 и равняется (см таблицу критических значений критерия Стьюдента) 2,57. Далее вычисляем по вышеуказанной формуле величину t в, которая в данном случае равна 2,54
Поскольку t в =2,54<2.57= tкр, то принимается гипотеза H0, т.е. можно говорить о несущественности связи на уровне значимости 0.05. В этом случае можно понизить уровень значимости до 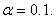
tкр=2.02 и t в =2,54>2,02=tкр
Следовательно, гипотеза H0 на уровне значимости α=0,1 отвергается, и связь можно считать существенной.
«Замечание к применению метрических коэффициентов ». Из гл.10 книги А.Д.Наследова «Математические методы психологического исследования»
Если связь (статистически достоверная) не обнаружена, но есть основания предполагать что связь на самом деле есть, то следует проверить возможные причины недостоверности связи.
1) Нелинейность связи: посмотреть график двумерного рассеивания. Если связь нелинейная, но монотонная, перейти к ранговым корреляциям. Если связь не монотонная, то делить выборку на части, в которых связь монотонная, и вычислить корреляции для отдельной части выборки, или делить выборку на контрастные группы и далее сравнивать по уровню выраженности признака.
2) Наличие выбросов ( Выбросом называется экспериментальная точка, удаленная от основной массы значений, то есть экстремально большие или малые значения признака.) и выраженная асимметрия распределения одного или обоих признаков. Просмотреть гистограммы распределения частот того и другого признака. При наличии выбросов или асимметрии исключить выбросы и перейти к ранговым корреляциям
3) Неоднородность выборки: просмотреть график двумерного рассеивания. Попытаться разделить выборку на части, в которых связь может иметь разные направления.
Если связь статистически достоверна, то прежде, чем делать содержательные выводы, следует исключить возможности «ложной» корреляции
1) Связь обусловлена выбросами: просмотреть график двумерного рассеивания. При наличии выбросов перейти к ранговым корреляциям или исключить выбросы.
2) Связь обусловлена влиянием третьей переменной: просмотреть график двумерного рассеивания на предмет наличия содержательно интерпретируемого деления выборки на группы, для которых согласованно меняются средние двух переменных. Если подобное явление возможно, необходимо вычислить корреляцию не только для всей выборки, но и для каждой группы в отдельности. Если «третья» переменная – метрическая – вычислить частную корреляцию.
Дополнение. Из книги Г.Секей «Парадоксы теории вероятностей и математической статистики», глава II «Парадоксы статистики», §5. Парадоксы корреляции






|
|
|


