Связь между напряженностью электрического поля и потенциалом.

ЭЛЕКТРОСТАТИКА

1.ЭЛЕКТРИЧЕСКИЙ ЗАРЯД – это физическая величина, характеризующая свойство частиц или тел вступать в электромагнитные силовые взаимодействия.

Существует два рода электрических зарядов, условно названных положительными и отрицательными.

Заряды могут передаваться (например, при непосредственном контакте) от одного тела к другому. В отличие от массы тела электрический заряд не является неотъемлемой характеристикой данного тела. Одно и то же тело в разных условиях может иметь разный заряд.

Одноименные заряды отталкиваются, разноименные – притягиваются. В этом также проявляется принципиальное отличие электромагнитных сил от гравитационных. Гравитационные силы всегда являются силами притяжения.

Закон сохранения электрического заряда.

В изолированной системе алгебраическая сумма зарядов всех тел остается постоянной:

q1 + q2 + q3 +... +qn = const.

Электрический заряд – неотъемлемое свойство, присущее некоторым «простейшим» частицам материи – так называемым «элементарным» частицам. Электрический заряд вместе с массой, энергией, спином и т.д. образуют «комплекс» фундаментальных свойств частиц.

Из известных в настоящее время элементарных частиц электрическим зарядом обладают электроны, позитроны, протоны, антипротоны, некоторые мезоны и гипероны и их античастицы. Не обладают электрическим зарядом нейтроны, нейтрино, нейтральные мезоны и гипероны и их античастицы, а также фотоны.

2 Известны только два рода электрических зарядов, условно называемых положительными и отрицательными (термины «положительное» и «отрицательное» электричество впервые введены В. Франклином (США) в XVIII в.).

3 Многочисленными опытами установлено, что абсолютная величина заряда всех заряженных элементарных частиц одинакова и равна 1,6 ⋅ 10–19 Кл. Этот минимальный электрический заряд (положительный или отрицательный) называется элементарным зарядом или атомом электричества.

Любой заряд q состоит из целого числа элементарных зарядов:

q = ± eN,

где e – абсолютная величина заряда; N – любое целое положительное число (1, 2, 3, …).

Изменение любого заряда может происходить только скачком, сразу на величину одного или нескольких элементарных зарядов.

Идея о дискретном, атомистическом строении электричества была выдвинута В. Вебером и Г. Гельмгольцем (Германия) во второй половине XIX в. Опытным обоснованием этой идеи было открытие законов электролиза (М. Фарадей, Англия) и исследование свойств катодных и анодных лучей (Крукс, Англия).

4 Если заряд q содержит весьма большое число элементарных зарядов, его называют макроскопическим. Изменение такого заряда можно считать непрерывным, так как элементарный заряд по сравнению с ним весьма мал.

5 Прямое экспериментальное определение величины элементарного заряда (заряда электрона) было впервые осуществлено в 1909 – 1914 гг. Р.Э. Милликеном (США) и А.Ф. Иоффе (Россия). После опытов Милликена и Иоффе была отвергнута выдвинутая было гипотеза о существовании субэлектронов, т.е. зарядов, меньших заряда электрона.

6 Электрический заряд неотделим от частиц, которым он принадлежит. Неуничтожимость материи влечет за собой неуничтожимость электрического заряда. К известным из механики и теоретической механики законам сохранения массы, импульса, момента импульса, энергии следует добавить закон сохранения электрического заряда: в замкнутой системе тел или частиц алгебраическая сумма зарядов есть величина постоянная, какие бы процессы не происходили в системе. Закон сохранения заряда был установлен экспериментально Ф. Эпинусом (Россия) и М. Фарадеем (Англия).

7 Все элементарные заряженные частицы всегда находятся в состоянии движения. Рассматриваемые в электростатике «неподвижные» заряды есть результат макроскопического усреднения: если геометрическая сумма скоростей всех элементарных зарядов, образующих данный макроскопический заряд q, в среднем равна нулю, то такой заряд проявляет себя в окружающем пространстве как «неподвижный».

8 Элементарные заряды, имеющиеся в телах, будем называть свободными, если заряженные частицы могут перемещаться по всему объему тела, и связанными, если они прочно связаны со своими атомами или молекулами.

9 Макроскопический заряд будем называть свободным, если он состоит из свободных элементарных зарядов, и связанным, если он состоит из связанных элементарных зарядов.

10 С движением любого элементарного заряда связано наличие электромагнитного микрополя.

Электрическое и магнитное поля, изучаемые электростатикой и макроскопической электродинамикой, являются усредненными: они представляют собой наложение (суперпозицию) микрополей, создаваемую большой совокупностью движущихся элементарных зарядов. Опыт показывает, что усредненное электрическое поле может быть отлично от нуля не только тогда, когда его «источник» – макрозаряд неподвижен, но и тогда, когда он движется. Усредненное магнитное поле отлично от нуля только тогда, когда создающий его макрозаряд находится в движении. Если макрозаряд неподвижен, то магнитные поля элементарных зарядов компенсируют друг друга, поэтому суммарное магнитное поле не обнаруживается и наблюдаемые явления выглядят как «чисто» электрические.

11 Предметом электростатики является изучение взаимодействия макроскопических зарядов, находящихся в условии равновесия, а также свойств электрических полей, связанных с такими зарядами.

Электрические поля, связанные с неподвижными зарядами, называются электростатическими, а электрические силы, характеризующие взаимодействие таких зарядов, – электростатическими или кулоновскими.

 

ПОТЕНЦИАЛ

Потенциальная энергия заряда в электрическом поле. Работу, совершаемую силами электрического поля при перемещении положительного точечного заряда q из положения 1 в положение 2, представим как изменение потенциальной энергии этого заряда:

,

где W _п1 и W _п2 – потенциальные энергии заряда q в положениях 1 и 2. При малом перемещении заряда q в поле, создаваемом положительным точечным зарядом Q, изменение потенциальной энергии равно

.

При конечном перемещении заряда q из положения 1 в положение 2, находящиеся на расстояниях r ₁ и r ₂ от заряда Q,

.

Если поле создано системой точечных зарядов Q ₁, Q ₂,¼, Q _n, то изменение потенциальной энергии заряда q в этом поле:

.

Приведённые формулы позволяют найти только изменение потенциальной энергии точечного заряда q, а не саму потенциальную энергию. Для определения потенциальной энергии необходимо условиться, в какой точке поля считать ее равной нулю. Для потенциальной энергии точечного заряда q, находящегося в электрическом поле, созданном другим точечным зарядом Q, получим

,

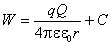где C – произвольная постоянная. Пусть потенциальная энергия равна нулю на бесконечно большом расстоянии от заряда Q (при r ® ¥), тогда постоянная C = 0 и предыдущее выражение принимает вид

.

При этом потенциальная энергия определяется как работа перемещения заряда силами поля из данной точки в бесконечно удаленную. В случае электрического поля, создаваемого системой точечных зарядов, потенциальная энергия заряда q:

.

Потенциальная энергия системы точечных зарядов. В случае электростатического поля потенциальная энергия служит мерой взаимодействия зарядов. Пусть в пространстве существует система точечных зарядов Q_i (i = 1, 2,..., n). Энергиявзаимодействия всех n зарядов определится соотношением

,

где r_ij - расстояние между соответствующими зарядами, а суммирование производится таким образом, чтобы взаимодействие между каждой парой зарядов учитывалось один раз.

Потенциал электростатического поля. Поле консервативной силы может быть описано не только векторной функцией, но эквивалентное описание этого поля можно получить, определив в каждой его точке подходящую скалярную величину. Для электростатического поля такой величиной является потенциал электростатического поля, определяемый как отношение потенциальной энергии пробного заряда q к величине этого заряда, j = W _п / q, откуда следует, что потенциал численно равен потенциальной энергии, которой обладает в данной точке поля единичный положительный заряд. Единицей измерения потенциала служит Вольт (1 В).

Потенциал поля точечного заряда Q в однородной изотропной среде с диэлектрической проницаемостью e:

3. НАПРЯЖЕННОСТЬ ЭЛЕКТРИЧЕСКОГО ПОЛЯ. Количественной характеристикой силового действия электрического поля на заряженные тела служит векторная величина E, называемая напряжённостью электрического поля.

E = F / q _пр.

Она определяется отношением силы F, действующей со стороны поля на точечный пробный заряд q _пр, помещенный в рассматриваемую точку поля, к величине этого заряда.

Понятие «пробный заряд» предполагает, что этот заряд не участвует в создании электрического поля и так мал, что не искажает его, т. е. не вызывает перераспределения в пространстве зарядов, создающих рассматриваемое поле. В системе СИ единицей напряженности служит 1 В / м, что эквивалентно 1 Н / Кл.

Электрическое поле. Для объяснения природы электрических взаимодействий заряженных тел необходимо допустить наличие в окружающем заряды пространстве физического агента, осуществляющего это взаимодействие. В соответствии с теорией близкодействия, утверждающей, что силовые взаимодействия между телами осуществляются через посредство особой материальной среды, окружающей взаимодействующие тела и передающей любые изменения таких взаимодействий в пространстве с конечной скоростью, таким агентом является электрическое поле.

Электрическое поле создается как неподвижными, так и движущимися зарядами. О наличии электрического поля можно судить, прежде всего, по его способности оказывать силовое действие на электрические заряды, движущиеся и неподвижные, а также по способности индуцировать электрические заряды на поверхности проводящих нейтральных тел.

Поле, создаваемое неподвижными электрическими зарядами, называют стационарным электрическим, или электростатическим полем. Оно представляет собой частный случай электромагнитного поля, посредством которого осуществляются силовые взаимодействия между электрически заряженными телами, движущимся в общем случае произвольным образом относительно системы отсчета.

Напряженность поля точечного заряда. Используя закон Кулона (1.1) найдем выражение для напряжённости электрического поля, создаваемого точечным зарядом q в однородной изотропной среде на расстоянии r от заряда:

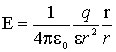(1.2)

В этой формуле r – радиус-вектор, соединяющий заряды q и q _пр. Из (1.2) следует, что напряжённость E поля точечного заряда q во всех точках поля направлена радиально от заряда при q > 0 и к заряду при q < 0.

ТЕОРЕМА ГАУССА.

Поток вектора напряженности электрического поля. Пусть небольшую площадку D S (рис.1.2) пересекают силовые линии электрического поля, направление которых составляет с нормалью n к этой площадке угол a. Полагая, что вектор напряженности Е не меняется в пределах площадки D S, определим поток вектора напряженности через площадку D S как

DF _E = E D S cos a. (1.3)

Поскольку густота силовых линий равна численному значению напряжённости E, то количество силовых линий, пересекающих площадку D S, будет численно равно значению потока DF _E через поверхность D S. Представим правую часть выражения (1.3) как скалярное произведение векторов E и D S = n D S, где n – единичный вектор нормали к поверхности D S. Для элементарной площадки d S выражение (1.3) принимает вид

dF _E = E d S

Через всю площадку S поток вектора напряженности вычисляется как интеграл по поверхности

Поток вектора электрической индукции. Поток вектора электрической индукцииопределяется аналогично потоку вектора напряженности электрического поля

dF _D = D d S

В определениях потоков заметна некоторая неоднозначность, связанная с тем, что для каждой поверхности можно задать двенормали противоположного направления. Для замкнутой поверхности положительной считается внешняя нормаль.

Теорема Гаусса. Рассмотрим точечный положительный электрический заряд q, находящийся внутри произвольной замкнутой поверхности S (рис. 1.3). Поток вектора индукции через элемент поверхности d S равен
(1.4)

Составляющую d S_D = d S cosa элемента поверхности d S в направлении вектора индукции D рассматриваем как элемент сферической поверхности радиуса r, в центре которой расположен заряд q.

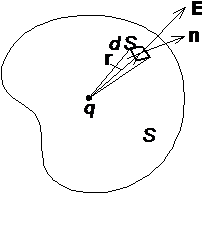
Учитывая, что d S_D / r ² равен элементарному телесному углу dw, под которым из точки нахождения заряда q виден элемент поверхности d S, преобразуем выражение (1.4) к виду dF _D = q dw / 4p, откуда после интегрирования по всему окружающему заряд пространству, т. е. в пределах телесного угла от 0 до 4p, получим

F _D = q.

Поток вектора электрической индукции через замкнутую поверхность произвольной формы равен заряду, заключенному внутри этой поверхности.

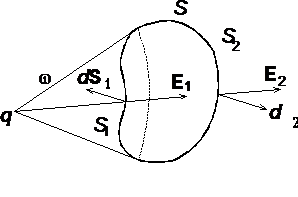
Если произвольная замкнутая поверхность S не охватывает точечный заряд q (рис. 1.4), то, построив коническую поверхность с вершиной в точке нахождения заряда, разделим поверхность S на две части: S ₁ и S ₂. Поток вектора D через поверхность S найдем как алгебраическую сумму потоков через поверхности S ₁ и S ₂:

.

Обе поверхности из точки нахождения заряда q видны под одним телесным угломw. Поэтому потоки равны

.

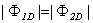Поскольку при вычислении потока через замкнутую поверхность используется внешняя нормаль к поверхности, легко видеть, что поток Ф _1D < 0, тогда как поток Ф _2D > 0. Суммарный поток Ф _D = 0. Это означает, что поток вектора электрической индукции через замкнутую поверхность произвольной формы не зависит от зарядов, расположенных вне этой поверхности.

Если электрическое поле создаётся системой точечных зарядов q ₁, q ₂,¼, q_n, которая охватывается замкнутой поверхностью S, то, в соответствии с принципом суперпозиции, поток вектора индукции через эту поверхность определяется как сумма потоков, создаваемых каждым из зарядов. Поток вектора электрической индукции через замкнутую поверхность произвольной формы равен алгебраической сумме зарядов, охваченных этой поверхностью:

(1.5)

Следует отметить, что заряды q_i не обязательно должны быть точечными, необходимое условие - заряженная область должна полностью охватываться поверхностью. Если в пространстве, ограниченном замкнутой поверхностью S, электрический заряд распределен непрерывно, то следует считать, что каждый элементарный объём d V имеет заряд . В этом случае в правой части выражения (1.5) алгебраическое суммирование зарядов заменяется интегрированием по объёму, заключённому внутри замкнутой поверхности S:

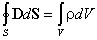(1.6)

Выражение (1.6) является наиболее общей формулировкой теоремы Гаусса: поток вектора электрической индукции через замкнутую поверхность произвольной формы равен суммарному заряду в объеме, охваченном этой поверхностью, и не зависит от зарядов, расположенных вне рассматриваемой поверхности. Теорему Гаусса можно записать и для потока вектора напряженности электрического поля:

_.

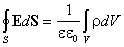Из теоремы Гаусса следует важное свойство электрического поля: силовые линии начинаются или заканчиваются только на электрических зарядах или уходят в бесконечность. Еще раз подчеркнем, что, несмотря на то, что напряжённость электрического поля E и электрическая индукция D зависят от расположения в пространстве всех зарядов, потоки этих векторов через произвольную замкнутую поверхность S определяются толькотеми зарядами, которые расположены внутри поверхности S.

Дифференциальная форма теоремы Гаусса. Отметим, что интегральная форма теоремы Гаусса характеризует соотношения между источниками электрического поля (зарядами) и характеристиками электрического поля (напряженностью или индукцией) в объеме V произвольной, но достаточной для формирования интегральных соотношений, величины. Производя деление объема V на малые объемы V_i , получим выражение

справедливое как в целом, так и для каждого слагаемого. Преобразуем полученное выражение следующим образом:

(1.7)

и рассмотрим предел, к которому стремится выражение в правой части равенства, заключенное в фигурных скобках, при неограниченном делении объема V. В математике этот предел называют дивергенцией вектора (в данном случае вектора электрической индукции D):

Дивергенция вектора D в декартовых координатах:

Таким образом выражение (1.7) преобразуется к виду:

_.

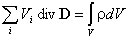Учитывая, что при неограниченном делении сумма в левой части последнего выражения переходит в объемный интеграл, получим

Полученное соотношение должно выполняться для любого произвольно выбранного объема V. Это возможно лишь в том случае, если значения подынтегральных функций в каждой точке пространства одинаковы. Следовательно, дивергенция вектора D связана с плотностью заряда в той же точке равенством

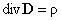
или для вектора напряженности электростатического поля

.

Эти равенства выражают теорему Гаусса в дифференциальной форме.

Отметим, что в процессе перехода к дифференциальной форме теоремы Гаусса получается соотношение, которое имеет общий характер:

_.

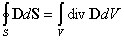Выражение называется формулой Гаусса - Остроградского и связывает интеграл по объему от дивергенции вектора с потоком этого вектора сквозь замкнутую поверхность, ограничивающую объем

СВЯЗЬ МЕЖДУ НАПРЯЖЕННОСТЬЮ ЭЛЕКТРИЧЕСКОГО ПОЛЯ И ПОТЕНЦИАЛОМ.

Для установления связи между силовой характеристикой электрического поля - напряжённостью и его энергетической характеристикой - потенциалом рассмотрим элементарную работу сил электрического поля на бесконечно малом перемещении точечного заряда q: d A = q E d l, эта же работа равна убыли потенциальной энергии заряда q: d A = - d W _п = - q d ,где d - изменение потенциала электрического поля на длине перемещения d l. Приравнивая правые части выражений, получаем: E d l = -d или в декартовой системе координат

E_x d x + E_y d y + E_z d z = -d , (1.8)

где E_x, E_y, E_z - проекции вектора напряженности на оси системы координат. Поскольку выражение (1.8) представляет собой полный дифференциал, то для проекций вектора напряженности имеем

откуда

.

Стоящее в скобках выражение является градиентом потенциала j, т. е.

E = - grad = -Ñ .

Напряжённость в какой-либо точке электрического поля равна градиенту потенциала в этой точке, взятому с обратным знаком. Знак «минус» указывает, что напряженность E направлена в сторону убывания потенциала.

Рассмотрим электрическое поле, создаваемое положительным точечным зарядом q (рис. 1.6). Потенциал поля в точке М, положение которой определяется радиус-вектором r, равен = q / 4pe₀e r. Направление радиус-вектора r совпадает с направлением вектора напряженности E, а градиент потенциала направлен в противоположную сторону. Проекция градиента на направление радиус-вектора

.

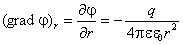Проекция же градиента потенциала на направление вектора t, перпендикулярного вектору r, равна

,

т. е. в этом направлении потенциал электрического поля является постоянной величиной ( = const).

В рассмотренном случае направление вектора r совпадает с направлением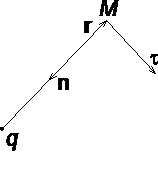
рис. 1.6

силовых линий. Обобщая полученный результат, можно утверждать, что во всех точках кривой, ортогональной к силовым линиям, потенциал электрического поля одинаков. Геометрическим местом точек с одинаковым потенциалом является эквипотенциальная поверхность, ортогональная к силовым линиям.

рис. 1.7

При графическом изображении электрических полей часто используют эквипотенциальные поверхности. Обычно эквипотенциали проводят таким образом, чтобы разность потенциалов между любыми двумя эквипотенциальными поверхностями была одинакова. На рис. 1.7 приведена двухмерная картина электрического поля. Силовые линии показаны сплошными линиями, эквипотенциали - штриховыми.

Подобное изображение позволяет сказать, в какую сторону направлен вектор напряжённости электрического поля; где напряжённость больше, где меньше; куда начнёт двигаться электрический заряд, помещённый в ту или иную точку поля. Так как все точки эквипотенциальной поверхности находятся при одинаковом потенциале, то перемещение заряда вдоль нее не требует работы. Это значит, что сила, действующая на заряд, все время перпендикулярна перемещению.

 

123456789Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: