 |
Векторы состояния в координатном представлении
|
|
|
|
Рассмотрим ради простоты одномерный случай: частица движется вдоль оси Ox.
Собственные векторы эрмитова оператора координаты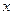 
являются базисными в координатном представлении. Обозначив их через 
, запишем уравнение для собственных векторов и собственных значений оператора :
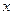(6.1)
Аналогично, собственный вектор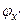 
, принадлежащий конкретному значению координаты 
, удовлетворяет уравнению:
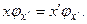(6.2)
Любой вектор Yгильбертова пространства, определяющий состояние одномерной квантовой системы, может быть разложен в интеграл Фурье по базисным векторам согласно формуле:
(6.3)
где коэффициенты разложения записываются в виде:
(6.4)
и представляют собою координаты вектора 
или его проекции на базисные векторы в координатном представлении.
Вектор 
обладает единичной нормой 
, причем норму вектора Y можно представить следующим выражением:
.
Этому условию можно удовлетворить, если считать, что собственные векторы оператора 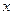с непрерывным спектром собственных значений нормируются на 
-функцию Дирака:
(6.5)
Тогда
(6.6)
т.е. в координатном представлении проекциями вектора Y являются значения комплексной функции 
при различных значениях 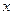, и что 
- вероятность обнаружения частицы с координатой 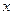из интервала 
. Следовательно, квадраты модулей коэффициентов Фурье-разложения (6.4) представляют известную формулу плотности вероятности 
.
Таким образом, совокупность проекций или координат Y–вектора определяет этот вектор Y в координатном представлении. Другими словами, множество проекций (координат) называют вектором состояния в координатном представлении или коротко волновой функцией.
Формула (6.5) свидетельствует об ортогональности собственных векторов эрмитова оператора :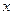
|
|
|
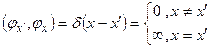, (6.7)
в то же время норма собственных векторов равна ∞.1
Определим скалярное произведение двух векторов y и c гильбертова пространства в координатном представлении. Записывая векторы y и c в форме разложения по базисным векторам в координатном представлении
получим
(6.8)
Эта формула является обобщением выражения скалярного произведения геометрических векторов на случай векторов гильбертова пространства.
Операторы физических величин в координатном
Представлении
Основная проблема квантовой механики - проблема квантования - связана с определением явного вида операторов физических величин.
Пусть некоторая физическая величина изображается линейным эрмитовым оператором 
, состояние же квантовой системы описывается вектором . В общем случае
, (6.9)
где 
.
В координатном представлении состояние квантовой системы описывается комплексной функцией координаты x:
y ® y(x), где y(x) = (jx,y),
c ® c(x), где c(x) = (jx, c).
Следовательно, оператор в координатном представлении каждой функции ставит в соответствие функцию 
:
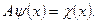(6.10)
Если учесть, что каждая физическая величина есть функция канонических переменных, т.е. 
, где 
(s - число степеней свободы), тогда согласно принципу соответствия соотношения между физическими величинами и каноническими переменными (координатами 
и обобщенными импульсами 
) переносятся на операторы физических величин.
Таким образом, очень важно установить явный вид операторов координат 
и проекций импульсов 
. Для этого прежде всего рассмотрим одномерную задачу.
Оператор координаты x в координатном представлении.
Пусть 
, тогда уравнение (6.9) примет вид:
(6.9`)
В координатном представлении это уравнение преобразуется в согласии с (6.10):
(6.10`)
Разложим векторы y и c в интеграл Фурье по базисным векторам , для которых справедливы уравнения (6.1), и подставим в левую часть уравнения (6.9`):
|
|
|
Тогда уравнение (6.10`) записывается в виде:
откуда
(6.11)
Сравнивая (6.10`) и (6.11), получаем
(6.12)
Следовательно, в координатном представлении оператор координаты 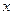есть сама координата 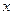, т.е. оператор 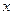в координатном представлении есть простая операция умножения на эту координату.
Аналогичным образом можно показать, что
т.е. 
(6.13)
Оператор 
в координатном представлении.
Для частицы, движущейся вдоль оси ,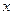 
. Пусть эта физическая величина изображается эрмитовым оператором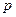 
. Запишем уравнение для собственных векторов и собственных значений этого оператора :
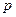(6.14)
Для конкретного значения импульса 
это уравнение имеет вид:
(6.14`)
Учтем, что в случае непрерывного спектра собственных значений оператора 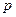собственные его векторы нормируются на -функцию Дирака:
(6.15)
Разложим вектор 
по собственным векторам оператора :
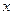(6.16)
где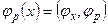 
- проекции собственных векторов , совокупность которых определяет вектор в координатном представлении, т.е. 
является волновой функцией частицы с заданной величиной импульса. Согласно гипотезе деБройля в качестве такой волновой функции следует взять плоскую монохроматическую волну 
Таким образом,
. (6.17)
Определим нормировочный коэффициент c, пользуясь условием (6.15):
Переходя к новой переменной интегрирования 
и учитывая определение - функции
(6.18)
для скалярного произведения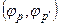 
получим следующий результат:
С учетом условия нормировки (6.15) находим:
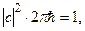
откуда
(6.19)
Следовательно, нормированная волновая функция частицы (6.19), движущейся вдоль оси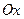 
с определенным импульсом , имеет вид:
1 (6.20)
Заметим, что
в то же время уравнение (6.14) позволяет записать
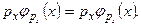
Из сравнения левых частей этих уравнений следует выражение для оператора в координатном представлении
. (6.21)
Правильный явный вид оператора 
в координатном представлении (6.21) подтверждают расчеты с произвольным вектором квантового состояния системы. Разложим для этого по собственным векторам оператора 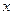, а затем по собственным векторам оператора :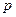
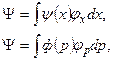
где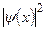 
- плотность вероятности обнаружения у частицы координаты , 
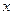- плотность вероятности обнаружения у частицы импульса 
.
Тогда волновая функция с учетом (6.17) может быть представлена в виде:
|
|
|
(6.22)
Действуя оператором на волновую функцию 
, получим:
.
Зная явный вид оператора проекций импульса в координатном представлении, подобным образом можно доказать справедливость аналогичных выражений для операторов 
, т.е.
. (6.23)
|
|
|
