и энергии через векторный потенциал

 

Магнитный поток через индукцию

 

Используя теорему Стокса, получим:

. (4.16)

.

Согласно магнитный поток 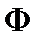сквозь поверхность равен линейному интегралу от векторного потенциала по замкнутому контуру, ограничивающему эту поверхность.

Рис.4.1

Для вычисления магнитного потока по формуле (4.16) достаточно знать векторный потенциал только на контуре, ограничивающем эту поверхность, т.е. интегрирование по поверхности заменяется интегрированием по контуру, что во многих случаях значительно упрощает расчеты. Сравнивая (4.16) и первое уравнение (4.2), можно провести формальное сопоставление (4.16) с законом полного тока, примененным к одиночному проводу с током : линии вектора охватывают магнитный поток подобно тому, как линии вектора в однородной среде охватывают ток (рис. 4.1).

 

Известно, что с магнитным полем связана энергия, распределенная в пространстве с плотностью

, так как В = μН.

В некоторой области V она определяется интегралом

, так как .

Используя равенство получим

Преобразуем второе слагаемое по теореме Остроградского-Гаусса

При учете всей энергии поля подынтегральное выражение в последней формуле устремляется к нулю так как векторный потенциал и напряжение магнитного поля убывают быстрее, чем r ^–2, а площадь увеличивается пропорционально r ². Таким образом, с учетом получаем:

.

 

Необходимо отметить, что величина не является плотностью энергии. Если предположить, что – плотность энергии магнитного поля, то немедленно следует, что вся энергия магнитного поля заключена в области, где (например, в проводах). Однако физически данное утверждение неверно, так как энергией обладают все точки, где , т.е. не только в области, где , но и вне ее (не только в проводах, но и вокруг них). Выражение (4.18) просто устанавливает связь между энергией поля и векторным потенциалом .

Для системы контуров с токами, ограничивающих объемы (рис. 4.2), энергию магнитного поля можно рассчитать по формуле

.

 

Рис. 4.2

 

Если контуры образованы линейными проводниками (линейные контуры), меняя на и переходя к интегралу по контуру , получим:

. (4.17)

С учетом (4.16) выражение (7.17) примет вид

, (4.18)

где – постоянный ток, протекающий по -му линейному контуру.

Формула (4.18) определяет магнитную энергию взаимодействия линейных контуров с токами (энергию магнитного поля, созданного системой контуров с токами).

 

4.4.Граничные условия в магнитном поле

 

Система дифференциальных уравнений поля является математической записью законов магнитного поля постоянного тока для областей, в которых функции , , и непрерывны и дифференцируемы. На границе раздела сред с разными магнитными свойствами эти функции терпят разрыв. Найдем общие условия, которым подчиняются составляющие векторов магнитной индукции и напряженности поля на границе двух сред с различными абсолютными магнитными проницаемостями m₁ и m_2.

Получим математическую запись законов поля на границе раздела сред, или граничные условия.

Обе среды будем предполагать однородными и изотропными. Пусть q₁ и q₂ – углы между направлением линии магнитной индукции и направлением нормали к поверхности раздела в первой и во второй среде (рис. 4.3, а). Составим линейный интеграл вектора Н по контуру abcda, стороны которого ab и cd лежат в разных средах бесконечно близко к поверхности раздела.

Имеем: 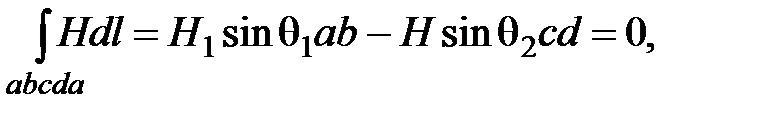т.к. сквозь поверхность, ограниченную контуром интегрирования, не проходит электрический ток. Принимая во внимание, что ab = cd, получаем H₁sinq₁ = H₂sinq₂ или

.

На поверхности раздела равны касательные составляющие вектора напряженности магнитного поля.

 

Представим себе замкнутую поверхность, образованную двумя плоскими поверхностями s₁ и s₂, следы которых в плоскости рисунка суть линии ab и cd, и цилиндрической поверхностью, пересекающейся с плоскостью рисунка по линиям bc и ad. Магнитный поток сквозь эту поверхность равен нулю.

Следовательно, откуда, приняв во внимание, что s₁ = s₂ находим:

или

,

т.е., на поверхности раздела равны нормальные составляющие вектора В.

Из условий на поверхности раздела для векторов Н и В имеем:

или

Большое практическое значение имеет вопрос о характере магнитного поля в воздухе около поверхности стальных частей машин, трансформаторов, электромагнитов и других электротехнических устройств. Магнитные проницаемости ферромагнитной среды и воздуха сильно разнятся между собой. Для воздуха практически m₂ = m₀. Пусть для ферромагнитной среды m₁ = 1000m₀. В таком случае имеем: tgq₁ = 1000 tgq₂. Если линии магнитной индукции внутри ферромагнитной среды (рис. 4.3, б) составляют с нормалью угол q₁ = 89^°, то соответствующий угол в воздухе оказывается равным q₂» 3^°20^’. Поэтому во всех случаях, когда магнитное поле создается токами, протекающими по проводникам, расположенным в воздухе, практически можно принять q₂ = 0, т.е. считать, что линии магнитной индукции в воздухе нормальны к поверхностям тел из ферромагнитных материалов.

 

 

4.3.1. Граничные условия для векторного потенциала

магнитного поля

При расчете используются граничные условия, выраженные через векторный потенциал. Условие записывается в виде , а условие - в виде

.

На поверхности тела с идеальными магнитными свойствами

() при отсутствии на них поверхностных токов справедливы на них условия ® .

4.3. Скалярный потенциал магнитного поля

 

В той части пространства, где плотность тока равна нулю, имеем rot = 0 и, следовательно, в этой части пространства можно представить напряженность магнитного поля в виде = –gradj_м.

Из сказанного ясно, что пользоваться понятием скалярного магнитного потенциала можно только в той области пространства, где = 0. Однако и в этой части пространства j_м является многозначной функцией. Линейный интеграл напряженности магнитного поля, взятый по любому замкнутому контуру, не охватывающему контура с током, равен нулю:

Рис.4.4

 

 

Если выбрать такой замкнутый путь интегрирования, который охватывает контур тока i, например, путь AlBmA на рис.4.4, то линейный интеграл напряженности магнитного поля по такому пути уже не равен нулю:

откуда

Путь ArBmA охватывает два раза контур с током i. Для такого пути имеем: и, следовательно, и вообще интеграл по некоторому пути AxB может отличаться от интеграла по пути AmB на ki, где k – целое число, если все пути проходят вне области пространства, занятой самими проводниками с током:

Таким образом, скалярный магнитный потенциал оказывается величиной многозначной.

В соответствии с четвертым уравнением Максвелла divH = 0 и уравнением H= –gradφм скалярный магнитный потенциал подчиняется уравнению Лапласа:

.

Скалярную функцию называют скалярным потенциалом магнитного поля, или скалярным магнитным потенциалом, в отличие от векторного потенциала .

Применение понятия скалярного потенциала j _м в ряде случаев зна­чительно уп­рощает решение задач по расчету магнитного поля вне токов. Скалярный магнитный потенциал не имеет физического смысла, он служит удобной математической величиной для расчета магнитного поля.

 

4.3. Магнитное поле цилиндрического проводника с током

 

Пусть по бесконечно длинному цилиндрическому проводу радиуса R про­текает по­стоянный ток I. Выберем систему координат x, y, z так, чтобы ось про­вода совпадала с осью координат z.

Будем считать, что ток равномерно распределяется по сечению провода, тогда его плотность будет равна .

Имеем две об­ласти, для каж­дой из которых выполним расчет параметров магнитного поля:

1) область внутри провода при 0 £ r £ R,

2) область вне провода при R £ r £ ¥.

Для расчета поля во внутренней области выберем контур интегрирования в виде ок­ружности с текущим радиусом r < R. Тогда ток внутри контура интег­рирования:

, откуда .

Применим к контуру интегрирования закон полного тока в интеграль­ной форме:

,

откуда следует и .

Векторы и направлены по касательной к окружности, их направле­ние опре­деляется по правилу правоходового винта.

При увеличении радиуса на элементарную величину dr произойдет приращение магнитного потока на величину dj на единицу длины провода

(l = 1) и приращение магнитного потокосцепления на величину dy:

 

 

Внутренний магнитный поток и внутреннее потокосцепление найдутся в резуль­тате интегрирования полученных выше выражений по всему сечению провода:

_,

.

Из последнего уравнения следует формула для внутренней индуктив­ности провода на еди­ницу длины:

[Гн/м].

 

Внутренняя индуктивность провода зависит от его магнитной прони­цаемости m (для стальных проводов она значительно больше, чем для медных или алюминиевых) и не зави­сит от его радиуса.

Для расчета поля во внешней области выберем контур интегрирования в виде окруж­ности с текущим радиусом r > R. Ток внутри контура интегрирова­ния равен I и не зависит от текущего значения радиуса r. Из закона полного тока следует:

,

откуда

и .

 

Для магнитного поля снаружи провода можно определить скалярный магнитный потенциал, полагая Н = – gradφ_M..

В цилиндрической системе координат

Тогда

т.е. плоскости равного скалярного потенциала проходят через радиус и ось проводника.

 

4.4.Магнитное поле коаксиального кабеля

 

По кабелю замыкается ток I. Рассчитать поле и индуктивность коаксиального кабеля.

Снаружи кабеля поле отсутствует, так как SI = 0.

Таким образом, можно выделить три различные области с магнитными проницаемостями m₁, m₂, m₃.

Для расчета поля используем закон полного тока: = SI.

1. Область I – 0 < r < r ₁: = H ·2 pr;

SI = I ; H = 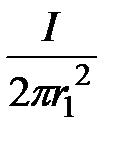· r; B = m ₁· H = · r; dФ = B · dS = · r · l · dr.

Так как во внутреннем проводнике магнитный поток dФ сцеплен только с частью тока I, которая пропорциональна отношению r ²/ r ₁², то магнитное потокосцепление dY = dФ · .

Рис.4.5

Внутренняя индуктивность первой области вычисляется по формуле

l ₁ = = = · = · =

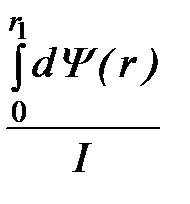и, как видим, не зависит от радиуса жилы.

2. Область II – r ₁ < r < r ₂.

SI = I; H = ; B = ; dY = dФ = B · dS = · l · dr.

внешняя индуктивность l ₂ = = ln .

3. Область III – r ₂ < r < r ₃.

SI = I – I ; H = ; B = ; dФ = · l · dr.

Этот поток сцеплен с током I и частью обратного тока, равной I .

Поэтому элементарное потокосцепление

dY = dФ · = dФ · .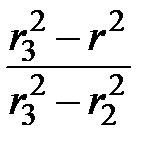

Внутренняя индуктивность третьей области:

l ₃ = = =

= · [ – 2 r + ] =

= · [r ln – r (r – r ) + (r – r )] =

= [ ln – ].

Внешняя индуктивность кабеля – l_е = l ₂; внутренняя индуктивность – l_i = l ₁ + l ₃;

вся индуктивность – l = l ₁ + l ₂ + l ₃.

Примерный график зависимости Н(r) представлен на рис. 4.6

Рис.4.6

4.5. Поток вектора Пойтинга в коаксиальном кабеле

 

Теорема Умова-Пойтинга позволяет сделать важный теоретический вы­вод, что элек­трическая энергия от генератора к приемнику передается не по проводам линии электропере­дачи, а электромагнитным полем, окружающим эти провода, а сами провода выполняют две другие функции:

1) создают усло­вия для получения электромагнитного поля;

2) являются на­правляющими для потока электроэнергии.

 

К кабелю прило­жено постоянное напряжение U и протекает ток I.

Особенностью режима работы коаксиального кабеля является то, что его электриче­ское и магнитное поле не выходит за пределы наружной оболочки.

Рассмотрим режим точки 1, расположенной в диэлектрике на расстоянии r от оси ка­беля. Линейная плотность заряда: .

Радиальная составляющая напряженности электрического поля: .

Вектор напряженности магнитного поля имеет только угловую составляющую: .

Векторы поля и направлены под углом в 90^о друг к другу.

Вектор Пойтинга: .

По­ток вектора Пойтинга через поперечное сечение диэлектрика:

.

Вывод: поток вектора Пойтинга через поперечное сечение диэлектрика равен переда­ваемой мощности Р, т. е. энергия от источника к приемнику передается электромагнит­ным полем, сосредоточенным в диэлектрике между жилой и оболочкой.

Рассмотрим режим точки 2, расположенной на наружной поверхности жилы.

Плотность тока в жиле кабеля: .

Составляющая напряженности электрического поля по оси z: .

Напряженность магнитного поля: .

Векторы поля и направлены под углом в 90^о друг к другу.

Радиальная составляющая вектора Пойтинга: .

Поток вектора Пойтинга через боковую поверхность внутренней жилы:

.

Вывод: поток вектора Пойтинга через наружную поверхность жилы направлен внутрь провода и равен мощности тепловых потерь в жиле .

 

4.6. Магнитное поле и индуктивность двухпроводной линии

 

Результирующий вектор магнитной индукции в произвольной точке n можно определить по методу наложения как геометрическую сумму

 

составляющих этого вектора 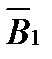и от каждого провода в отдельности:

= + . Составляющие вектора и определяются по полученным ранее формулам, а их направления – по правилу правоходового винта:

, .

Индуктивность линии равна L = 2(L_вн + L_сн). Для определения индуктивности проводника найдем величину тока через сечение радиусом r

и соответственно, по закону полного тока напряженность магнитного поля

Тогда потокосцепление

И внутренняя индуктивность проводника .

Рис.4.7

Определим потокосцепление между проводниками

Тогда

Таким образом, индуктивность двухпроводной линии равна

[ Гн / м ]

 

Индуктивность трехфазной линии на одну фазу.

 

В схемах замещения трехфазных линий электропередачи учитывается индуктивность одного провода (фазы), следовательно:

[Гн / м] – индуктивность каждого провода (фазы) трехфазной транспонированной ЛЭП на единицу длины, где – среднегеометрическое значение межосевых расстояний проводов.

 

 

4.7. Взаимная индуктивность двух параллельных линий

 

Пусть задано геометрическое расположение проводов в пространстве двух параллельных двухпроводных линий (1 и 1¢ - прямой и обратный провода первой линии, 2 и 2¢ - прямой и обратный провода второй линии).

Предположим, что по 1-й линии протекает постоянный ток I. Магнитный поток от провода 1, пересекающий плоскость второй линии, определится по формуле:

.

Магнитный поток от провода 1', пересекающий плоскость второй линии:

.

 

Как следует из рисунка, магнитные потоки Ф ₁ и Ф _1¢ в плоскости второй линии направлены одинаково, т.е. складываются. Результирующий магнитный поток взаимной индукции будет равен:

Взаимная индуктивность двух линий на единицу длины будет равна:

При использовании данного уравнения для расчетов следует учитывать, что индексы при расстояниях d зависят, во-первых, от обозначения проводов на чертеже, и во-вторых, от взаимной ориентации магнитных потоков Ф ₁ и Ф’ ₁, и в каждом конкретном случае должны устанавливаться индивидуально.

 

4.8.Соответствия электростатического (электрического) поля и магнитного поля постоянного тока в областях, не занятых током

 

Проведем сравнение основных уравнений, соотношений и граничных условий для электростатического поля в области, где нет свободных зарядов (), электрического поля в проводящей среде при отсутствии сторонних сил (), а также магнитного поля постоянного тока в области, где нет токов (), в однородной изотропной среде. Результаты сравнения представлены в табл.4.1. В табл. 4.2 приведены математически аналогичные величины, характеризующие стационарные электрические и магнитное поля.

 

Т а б л и ц а 4.1

 

№ п/п	Электростатическое поле ()	Электрическое поле в проводящей среде ()	Магнитное поле постоянного тока ()
	,	,	,
	,	,	,
			,
	,	,	,
	1) 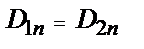, 2) .	1) , 2) .	1) , 2) .

 

 

Т а б л и ц а 4.2

 

Электростатическое поле ()		Электрическое поле в проводящей среде ()		Магнитное поле постоянного тока ()

 

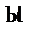
Здесь необходимо также упомянуть о двух типах взаимного соответствия электростатического (электрического) поля и магнитного поля постоянного тока в областях, не занятых током. Первый тип соответствия возникает, когда распределения линейных зарядов в электростатическом поле и линейных токов в магнитном поле одинаковы. В этом случае одинаковы и картины электростатического и магнитного полей (рис. 4.4). Различие между ними заключается лишь в том, что на месте линий напряженности электрического поля располагаются линии равного магнитного потенциала и на месте линий равного электрического потенциала располагаются линии напряженности магнитного поля.

Рис. 4.4

 

Второй тип соответствия возникает, когда одинакова форма граничных эквипотенциальных поверхностей в электростатическом поле и в магнитном поле постоянного тока. В этом случае картины поля оказываются совершенно одинаковыми.

Соответствие второго типа показано на рисунке ниже. На нем изображена картина магнитного поля в воздушном промежутке между полюсом и якорем машины постоянного тока. Если допустить, что полюс и якорь этой машины используют в качестве электродов некоторого конденсатора, то картина электрического поля в воздушном промежутке между электродами соответствовала бы картине магнитного поля.

 

Рассмотренные свойства магнитного поля постоянного тока расширяют область применения метода электростатической аналогии:

при расчете магнитного поля в области вне проводников с постоянными токами можно воспользоваться готовыми аналитическими решениями соответствующих задач электростатики и электрического поля в проводящей среде.

 

4.9. Графический метод построения картины поля

 

В сложных случаях аналитический расчет поля оказывается невозможным и приходится прибегать к приближенным графическим методам построения картины поля. Такой метод весьма полезен при построении картины поля около стальных полюсов электрических машин и аппаратов. На помощь нам при этом приходит то обстоятельство, что линии магнитной индукции в воздухе около полюсов нормальны к их поверхностям, и, следовательно, поверхности полюсов можно считать поверхностями равного магнитного потенциала. Такое условие верно в том случае, когда поле создается токами, проходящими по проводникам и обмоткам, расположенным в воздухе, что обычно и имеет место. Установим сначала метод построения картины поля в области, не занятой проводниками с токами, создающими исследуемое поле, т.е. около тех частей полюсов, которые выступают за пределы обмоток с током, наложенных на сердечники полюсов. Если, помимо того, в данной области пространства поле приближенно можно считать плоскопараллельным, то, очевидно, следует руководствоваться правилами, аналогичными тем, которые были установлены ранее для построения электрического поля, а именно:

1) линии напряженности поля и линии равного магнитного потенциала должны пересекаться всюду под прямым углом;

2) поверхности ферромагнитных сред следует считать поверхностями равного магнитного потенциала и линии напряженности поля в воздухе следует проводить перпендикулярно к ним;

3) ячейки сетки, образованной линиями напряженности поля и линиями равного потенциала, при достаточной густоте сетки должны быть приблизительно подобны друг другу.

Обозначим средние размеры ячейки сетки в направлении линии напряженности поля через Dn и в направлении линии равного магнитного потенциала через Da. Тогда последнее правило можно выразить в форме

Путем ряда последовательных приближений удается нарисовать картину поля, удовлетворяющую всем указанным требованиям. На рис. 4.8 построена таким способом картина поля около полюсов электрической машины.

∆ n

∆ a

 

Если построена картина поля, то из нее может быть найдено магнитное сопротивление R_м или магнитная проводимость воздушного промежутка между полюсом и якорем, причем F – магнитный поток в рассматриваемом промежутке и F – МДС на длине промежутка. Если m₁ – число трубок магнитной индукции, то F = m₁DF = m₁lm₀HDa, где DF – поток в одной трубке и l – длина в направлении оси z (перпендикулярной плоскости рисунка). Если m₂ – число интервалов между соседними линиями равного потенциала, то F = m₂DU_м = m₂HDn, где DU_м – изменение потенциала на протяжении одного интервала.

Таким образом,

Величина l представляет собой магнитную проводимость на единицу длины в направлении оси z. Она зависит исключительно от конфигурации рассматриваемого участка магнитной цепи.

Приведенные правила построения картины поля справедливы только в области, не занятой электрическим током. В области, где расположены проводники или катушки с током, эти правила неприменимы, так как здесь теряет смысл понятия скалярного магнитного потенциала.

 

4.10.Поле токов вблизи плоских поверхностей ферромагнитныхтел. Метод зеркальных изображений

Пусть около бесконечной плоскости, ограничивающей ферромагнитную среду, для которой примем ,расположен в воздухе параллельно плоскости провод с током i. Поверхность ферромагнитной среды является поверхностью равного магнитного потенциала, так как линии напряженности поля в воздухе к ней перпендикулярны.

Заменим мысленно ферромагнитную среду воздухом и током , являющимся зеркальным изображением в поверхности раздела действительного тока i. Ток примем равным току i и имеющим то же направление.

Средняя плоскость между действительным током и его зеркальным изображением, совпадающая с поверхность раздела сред в действительной задаче, является плоскостью равного ма

⇐ Предыдущая123

Поделиться:

Воспользуйтесь поиском по сайту: