 |
Приложения операционного исчисления.
|
|
|
|
1.Задача Коши для обыкновенного линейного дифференциального уравнения с постоянными коэффициентами:
x (n) + a 1 x (n - 1) + a 2 x (n - 2) + … + an - 1 x ′ + anx = f (t),
x (0) = x 0, x ′ (0) = x 1, x ″ (0) = x 2, …, x (n -1) (0) = xn -1.
Начальные условия в этой задаче заданы в точке t 0 = 0. Если начальные условия задаются в другой точке t 0 ≠ 0, то заменой аргумента u = t - t 0 их сдвигают в точку u 0 = 0.
Метод решения этой задачи основан на теореме о дифференцировании оригинала.
2.Общее решение дифференциального уравнения с постоянными коэффициентами.
3. Краевая задача для обыкновенного линейного дифференциального уравнения с постоянными коэффициентами. Если найдено общее решение уравнения, оно может быть использовано для решения краевой задачи. Пусть, например, задана краевая задача x ″ − 2 x ′ + x = e t, x (1) = x 1, x ′(3) = x 2, где x (1), x (2) - известные числа. Так как общее решение уже известно: 
, остаётся найти значения произвольных постоянных, при которых выполняются краевые условия: 
следовательно, решение краевой задачи равно
4. Уравнения с импульсной и составной правой частью. Это, возможно, единственный случай, когда операционное исчисление имеет преимущество перед другими методами решения рассматриваемых задач. Теорема запаздывания (20.2.4) позволяет полностью сохранить изложенный порядок действий.
5. Формулы Дюамеля. При решении задачи Коши для обыкновенного дифференциального уравнения согласно тому порядку действий, который изложен выше, необходимо находить изображение правой части уравнения, что в некоторых случаях может быть затруднительно или вообще невозможно. Формулы Дюамеля позволяют находить решение, не выписывая в явной форме изображение правой части.
|
|
|
,
.
№60
Интегралы, зависящие от параметров, их дифференцирование.
№61
№62
№63
Численное интегрирование.
Определенным интегралом функции f(x), взятом в интервале от a до b, называется предел, к которому стремится интегральная сумма 
при стремлении всех промежутков ∆xi к нулю 
. При приближенном вычислении определенного интеграла шаг интегрирования h=∆x выбирается конечным: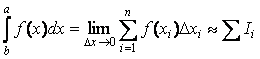 
, где Ii - элемент интегральной суммы. Заменяя подынтегральную функцию на каждом шаге отрезками линий нулевого, первого и второго порядков, получаем приближенные формулы для вычисления интеграла методами прямоугольников, трапеций и Симпсона соответственно.
1)
Правило прямоугольников (n=0). Заменяем график функции F(x) горизонтальной линией (линий нулевого порядка) и вычисляем значение элемента интегральной суммы как площадь прямоугольника 
, где h - шаг интегрирования, у0 - значение функции в точке х=х0, у(х0)=у0
2)
Правило трапеций (n=1). Заменяем график функции F(x) прямой, проходящей через две точки (х0,у0) и (х0+h,у1), и вычисляем значение элемента интегральной суммы как площадь трапеции 
3) 
Правило Симпсона (n=2).
Правило Симпсона (n=2). Заменяем график функции F(x) квадратичной параболой, проходящей через три точки с координатами (х0,у0), (х0+h,у1), (х0+2h,у2). Расчетную формулу для вычисления элемента интегральной суммы получим, используя интерполяционный многочлен Лагранжа, в виде y(x)=y0A0(x)+y1A1(x)+y2A2(x), где
При x0=0; x1=h; x2=2h, получим
.
При интегрировании на отрезке [a,b] расчетные формулы для методов прямоугольника, трапеций и Симпсона имеют вид
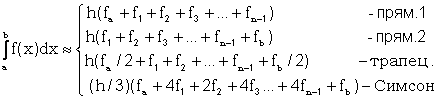, где h - шаг по x, fa, fi, fb - значения функции при x равном a, xi, b соответственно. Для метода прямоугольников приведены две расчетные формулы, так как площадь прямоугольника на каждом шаге интегрирования может определяться по левой или правой стороне. Суть метода прямоугольников для отрезка [a,b] проиллюстрирована на рисунке, при этом площадь под кривой f(x) (вспомните геометрический смысл определенного интеграла) заменена суммой площадей заштрихованных прямоугольников.
|
|
|
№64
|
|
|
