 |
Проверка статистических свойств остатков (качества оценок коэффициентов регрессии)
|
|
|
|
| По статистическим данным нельзя получить точные оценки неизвестныхкоэффициентов регрессии, но можно найти их приближенные оценки, качество которых характеризуется следующими тремя свойствами: · несмещенностью (каждый параметр регрессии можно рассматривать как среднее значение из возможного большого количества оценок); · эффективностью (оценки параметров характеризуются наименьшей дисперсией, что в практических исследованиях означает возможность перехода от точечного оценивания к интервальному; · состоятельностью (характеризует увеличение точности оценок с увеличением объема выборки). Метод наименьших квадратов обеспечивает указанные свойства оценкам параметров регрессии при выполнении следующих предположений: 1) математическое ожидание случайной переменной равно нулю; 2) дисперсии наблюдений случайной переменной одинаковы (это условие называется условием гомоскедастичности); 3) независимостьзначенийслучайной переменной в любом наблюдении от ее значений во всех других наблюдениях. Предположения 1–3 называются условиями Гаусса–Маркова. Теорема Гаусса–Маркова. Если условия 1–3 выполнены, то оценки коэффициентов парной линейной регрессии, полученные с помощью МНК, являются несмещенными, состоятельными и эффективными. |
4.4.1. Центрированность остатков: проверка выполнения условия 1 о равенстве математического ожидания остатков нулю
Оценкой математического ожидания случайной переменной М (e) является среднее остатков  Гипотеза о значимости математического ожидания случайной переменной проверяется с помощью t- статистики, наблюдаемое значение которой определяется равенством Гипотеза о значимости математического ожидания случайной переменной проверяется с помощью t- статистики, наблюдаемое значение которой определяется равенством  . По распреде- лению Стьюдента по заданному уровню значимости a и числу степеней свободы v = n – 1 находится критическая точка . По распреде- лению Стьюдента по заданному уровню значимости a и числу степеней свободы v = n – 1 находится критическая точка 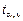 = tкр. Если tнабл > tкр, то М (e) значимо. Если tнабл < tкр, то М (e) незначимо.
Если условие 1 нарушено, то оценки коэффициентов регрессии могут быть смещенными, поэтому для устранения этих проблем в модель регрессии следует включать свободный член. = tкр. Если tнабл > tкр, то М (e) значимо. Если tнабл < tкр, то М (e) незначимо.
Если условие 1 нарушено, то оценки коэффициентов регрессии могут быть смещенными, поэтому для устранения этих проблем в модель регрессии следует включать свободный член.
|
|
|
|
Среднее из числовых характеристик остатков рассчитано на листе «Регрессия» и представлено в таблице 9.
Таблица 9 – Числовые характеристики остатков
| Условие 1 | |
| Остатки | |
| Среднее | –2,84E–14 |
| Стандартная ошибка | 0,76 |
| Медиана | –0,72 |
| Мода | #Н/Д |
| Стандартное отклонение | 3,40 |
| Дисперсия выборки | 11,58 |
| Эксцесс | 0,10 |
| Асимметричность | –0,36 |
| Интервал | 12,97 |
| Минимум | –7,84 |
| Максимум | 5,12 |
| Сумма | –5,68E–13 |
| Счет | |
| tнабл | –3,74E–14 |
| tкр | 2,09 |
Среднее остатков равно –2,84E–14 = –2,84∙10–14. Оно достаточно близко к нулю, поэтому можно предположить выполнимость условия 1 Гаусса–Маркова. Проверим значение среднего на значимость, т. е. гипотезу о равенстве нулю математического ожидания случайной переменной.
Сравним рассчитанные наблюдаемое и критическое значения статистики. Поскольку |tнабл| = 3,74E–14 = 3,74∙10–14 < tкр = 2,09, то среднее незначимо (т. е. незначительно отличается от нуля). Следовательно, условие 1 Гаусса–Маркова выполняется.
4.4.2. Гомоскедастичность (гетероскедастичность) остатков: проверка выполнения условия 2 о постоянстве и конечности дисперсии остатков, т. е. гомоскедастичности остатков
Предположение о постоянстве и конечности дисперсии остатков называется свойством гомоскедастичности остатков. Если оно не выполняется, то такое явление называется гетероскедастичностью. Гетероскедастичность часто вызывается ошибками спецификации, когда в модели не учитывается существенная переменная. Гетероскедастичность приводит к тому, что оценки коэффициентов регрессии не являются эффективными, увеличиваются дисперсии распределений оценок коэффициентов, появляется вероятность неверного вычисления оценок стандартных ошибок коэффициентов регрессии. В результате можно сделать неверный вывод о значимости коэффи- циента. Для оценки нарушения гомоскедастичности наиболее часто используются графический анализ отклонений, тест ранговой корреляции Спирмена и тест Голдфелда–Квандта.
При применении теста Спирмена предполагается, что абсолютные величины остатков и значения объясняющей переменной коррелированны. Эту корреляцию можно измерять с помощью коэффициента ранговой корреляции Спирмена по формуле
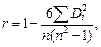 где Di – разность между рангом xi и рангом модуля остатка
где Di – разность между рангом xi и рангом модуля остатка  Тест проводится по следующей схеме:
· Строится линейная модель регрессии.
· Определяются ранги значений xi независимой переменной и соответствующие ранги модулей остатков
Тест проводится по следующей схеме:
· Строится линейная модель регрессии.
· Определяются ранги значений xi независимой переменной и соответствующие ранги модулей остатков  (ранг – это порядковый номер значения в ранжированном ряду).
· Находится коэффициент ранговой корреляции Спирмена.
· Осуществляется проверка гипотезы об отсутствии гетероскедастичности с помощью t- статистики, наблюдаемое значение которой определяется равенством (ранг – это порядковый номер значения в ранжированном ряду).
· Находится коэффициент ранговой корреляции Спирмена.
· Осуществляется проверка гипотезы об отсутствии гетероскедастичности с помощью t- статистики, наблюдаемое значение которой определяется равенством  Если tнабл > tкр, то гетероскедастичность присутствует. Значит, МНК-оценки неэффективны.
Поскольку M (e) равно нулю, то МНК-оценки параметров являются несмещенными и состоятельными, поэтому их позволительно использовать, например, для точечного прогнозирования даже в случае гетероскедастичности. Однако в этом случае МНК-оценки не являются эффективными, а следовательно, результаты (доверительные интервалы для коэффициентов и прогнозных значений), основанные на анализе дисперсии, неверны.
Существуют два подхода к решению проблемы гетероскедастичности:
· преобразование выборочных данных;
· применение взвешенного и обобщенного МНК (ОМНК).
Первый подход предполагает такое преобразование исходных данных, чтобы для них модель уже обладала свойством гомоскедастичности. Используют такие преобразования, как логарифмирование данных, переход к безразмерным величинам путем деления на некоторые известные величины той же размер- ности, что и исходные данные, стандартизация исходных данных.
Второй подход устранения гетероскедастичности состоит в построении моделей, учитывающих гетероскедастичность ошибок наблюдений. Если tнабл > tкр, то гетероскедастичность присутствует. Значит, МНК-оценки неэффективны.
Поскольку M (e) равно нулю, то МНК-оценки параметров являются несмещенными и состоятельными, поэтому их позволительно использовать, например, для точечного прогнозирования даже в случае гетероскедастичности. Однако в этом случае МНК-оценки не являются эффективными, а следовательно, результаты (доверительные интервалы для коэффициентов и прогнозных значений), основанные на анализе дисперсии, неверны.
Существуют два подхода к решению проблемы гетероскедастичности:
· преобразование выборочных данных;
· применение взвешенного и обобщенного МНК (ОМНК).
Первый подход предполагает такое преобразование исходных данных, чтобы для них модель уже обладала свойством гомоскедастичности. Используют такие преобразования, как логарифмирование данных, переход к безразмерным величинам путем деления на некоторые известные величины той же размер- ности, что и исходные данные, стандартизация исходных данных.
Второй подход устранения гетероскедастичности состоит в построении моделей, учитывающих гетероскедастичность ошибок наблюдений.
|
|
|
|
|
|
|
На листе «Условие 2» рассчитаны наблюдаемое и критическое значения t -статистики (таблица 10).
Таблица 10 – Проверка гипотезы об отсутствии гетероскедастичности
| tнабл | –1,25 |
| tкр | 2,10 |
Поскольку |tнабл| = 1,25 < tкр = 2,1, то гетероскедастичность отсутствует. Следовательно, условие 2 Гаусса–Маркова выполняется. Значит, МНК-оценки параметров регрессии будут эффективными. Поэтому модель можно использовать при точечном и интервальном прогнозировании.
4.4.3. Автокорреляция остатков: проверка выполнения условия 3 о независимости случайного члена в любом наблюдении от его значений во всех других наблюдениях
Условие 3 Гаусса–Маркова требует независимости значенийслучайной переменной в любом наблюдении от ее значений во всех других наблюдениях. Если данное условие не выполняется, то говорят, что случайная переменная подвержена автокорреляции. В этом случае коэффициенты регрессии, получаемые по МНК, оказываются неэффективными, хотяи несмещенными, а их стандартные ошибки рассчитываются некорректно (занижаются).
Существуют несколько методов определения автокорреляции остатков, два из которых приведены ниже.
Первый метод – это построение графика зависимостей остатков от номера наблюдений и визуальное определение наличия автокорреляции остатков (рисунок 7).
   
а бв г
Рисунок 7 – Модели зависимости остатков от номера наблюдения: случайные остатки (а); наличие зависимости в остатках (б), (в), (г)
Второй метод – проверка гипотезы об отсутствии автокорреляции остатков с помощью критерия Дарбина–Уотсона, т. е.
наблюдаемое значение которого рассчитывается как отношение суммы квадратов разностей последовательных значений остатков к сумме квадратов остатков.
Это же значение критерия может быть вычислено по формуле
где
Альтернативные гипотезы – гипотезы о наличии положительной или отрицательной автокорреляции в остатках. Если автокорреляция отсутствует, то Однако существуют области неопределенности, связанные с тем, что распределение статистики Дарбина–Уотсона зависит не только от числа наблюдений и числа объясняющих переменных, но и от значений объясняющих переменных. В этом случае используются другие способы проверки (например, визуальный и др.). По таблице, фрагмент которой приведен в таблице 11, определяются критические значения критерия Дарбина–Уотсона d 1 и d 2 для заданного числа наблюдений n, числа объясняющих переменных k и заданного уровня значимости 0,05.
Таблица 11 – Статистика Дарбина–Уотсона: d 1 и d 2 при уровне
По этим значениям отрезок [0; 4] разбивается на пять областей (рисунок 8).
0 Рисунок 8 – Критические области статистики Дарбина–Уотсона
В зависимости от того, в какую область попадает наблюдаемое значение критерия, принимают или отвергают гипотезу. |
На листе «Регрессия»в ячейке E47 рассчитано наблюдаемое значение d -статистики: dнабл = 1,38. По таблице критических значений d -ста-
тистики для числа наблюдений 20, числа объясняющих переменных
2 и заданного уровня значимости 0,05 значения d 1 = 1,10 и d 2 = 1,54, которые разбивают отрезок [0; 4] на пять областей (рисунок 9).
| Положительная автокорреляция | Область неопределенности | Автокорреляция отсутствует | Область неопределенности | Отрицательная автокорреляция |
0 1,10 1,54 2,46 2,90 4
Рисунок 9 – Критические области d -статистики Дарбина–Уотсона
Поскольку 1,10 < dнабл = 1,38 < 1,54, т. е. наблюдаемое значение попало в зону неопределенности, то ничего нельзя сказать о наличии автокорреляции, используя критерий Дарбина–Уотсона.
Визуально наличие автокорреляции остатков можно определить по графику остатков, полученному на листе «Регрессия»(рисунок 10).
|
|

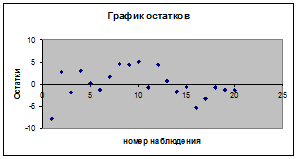
Рисунок 10 – График остатков
Поскольку на графике остатков точки разбросаны вдоль прямой
y = 0 хаотично без видимой закономерности, то зависимости между остатками не наблюдается. Поэтому условие 3 выполняется.
|
|
|
Анализ свойств модели
4.5.1. Мультиколлинеарность факторов: проверка мультиколлинеарности факторов
При построении уравнения множественной регрессии может возникнуть проблема мультиколлинеарности факторов, их тесной, линейной связанности. Считается, что две переменные явно коллинеарны, т. е. находятся между собой в линейной зависимости, если их парный коэффициент корреляции больше или равен 0,7. При наличии мультиколлинеарности МНК-оценки формально существуют, но обладают рядом недостатков. В частности, оценки имеют большие стандартные ошибки, малую значимость, в то время как модель в целом является значимой с высоким значением коэффициента детерминации.
Для отбора факторов в модель регрессии можно использовать корреляционную матрицу. Однако по величине парных коэффициентов корреляции обнаруживается лишь явная коллинеарность факторов. Поэтому при оценке мультиколлинеарности факторов предполагается использовать определитель D r матрицы парных коэффициентов корреляции между факторами.
Если бы факторы не коррелировали между собой, то матрица парных коэффициентов корреляции между факторами была бы единичной матрицей, поскольку все недиагональные элементы были бы равны нулю. Если же, наоборот, между факторами существует полная линейная зависимость и все коэффициенты корреляции равны 1, то определитель такой матрицы равен 0, т. е. D r = 0. Таким образом, чем ближе к 0 определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И, наоборот, чем ближе к 1 определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов.
Мультиколлинеарность факторов выявляется проверкой гипотезы H 0: D r = 1 с помощью статистики хи-квадрат с  степенями свободы. Наблюдаемое значение статистики определяется по формуле степенями свободы. Наблюдаемое значение статистики определяется по формуле
 где n – количество наблюдений;
p – число переменных.
Если
где n – количество наблюдений;
p – число переменных.
Если  то гипотеза H 0 отклоняется и наличие мультиколлинеарности объясняющих факторов считается доказанной. то гипотеза H 0 отклоняется и наличие мультиколлинеарности объясняющих факторов считается доказанной.
|
На листе «Исходные данные» найдены парные коэффициенты корреляции и определитель матрицы парных коэффициентов корреляции объясняющих факторов x 1 и x 2. Так как парный коэффициент корреляции факторов x 1 и x 2 r x 1, x 2 = 0,75 < 0,8, то зависимость между факторами существует, но она незначительная. Докажем это предположение проверкой гипотезы об отсутствии мультиколлинеарности с помощью статистики хи-квадрат, наблюдаемое и критическое значения которой найдены на листе «Регрессия» (таблица 12).
Таблица 12 – Мультиколлинеарность
| Мультиколлинеарность | |
| Определитель | 0,44 |
| хи-кв набл | 19,53 |
| хи-кв кр | 223,16 |
Поскольку хи-квадрат наблюдаемое равно 19,53 и меньше хи-квадрат критического, равного 223,16, то мультиколлинеарность факторов отсутствует.
4.5.2. Эластичность: оценка влияния каждого объясняющего фактора на результирующий фактор y
Частные средние коэффициенты эластичности показывают, на сколько процентов от среднего значения изменяется зависимая переменная с изменением на 1% фактора xj от своего среднего при фиксированном значении других факторов. Частные коэффициенты эластичности по каждой объясняющей переменной для линейной регрессии рассчитываются по формуле
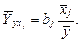
|
На листе «Исходные данные» найдены коэффициенты эластичности факторов – х1, х2 (таблица 13).
Таблица 13 – Эластичность факторов
| Эластичность | ||
| Фактор y_ср | Фактор х1_ср | Фактор х2_ср |
| 707,5215 | 32,85 | 11,1 |
| Коэффициент фактора x1 | 1,03 | |
| Эластичность фактора x1 | 0,05 | |
| Коэффициент фактора x2 | 9,28 | |
| Эластичность фактора x2 | 0,15 |
С изменением значения фактора x 1 на 1% при фиксированном значении фактора x 2 значение фактора y увеличивается на 0,05%. Аналогично с изменением значения фактора x 2 на 1% при фиксированном значении фактора x 1 значение фактора y увеличивается на 0,15%. Значит, влияние фактора x 2 больше, чем фактора x 1.
4.5.3. Частные коэффициенты корреляции: целесообразность включения в модель факторов, определение степени влияния факторов на результирующий фактор y при устранении влияния других факторов
Частные коэффициенты (или индексы) корреляции характеризуют тесноту связи между результатом и соответствующим фактором при неизменном уровне других факторов, включенных в уравнение регрессии. Они широко используются при решении проблемы отбора факторов, ранжировании факторов, участвующих в множественной линейной регрессии. При нелинейной взаимосвязи исследуемых признаков эту функцию выполняют частные индексы детерминации.
Порядок частного коэффициента корреляции определяется количеством факторов, влияние которых исключается. Например,  – коэффициент частной корреляции первого порядка для переменной x 1 при неизменном значении переменной x 2. Аналогично определяется – коэффициент частной корреляции первого порядка для переменной x 1 при неизменном значении переменной x 2. Аналогично определяется  через коэффициенты парной корреляции факторов.
Значимость частных коэффициентов корреляции оценивается с помощью t -статистики через коэффициенты парной корреляции факторов.
Значимость частных коэффициентов корреляции оценивается с помощью t -статистики 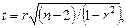 которая имеет распределение Стьюдента. Если которая имеет распределение Стьюдента. Если  то проверяемый коэффициент значим. то проверяемый коэффициент значим.
|
На листе «Исходные данные» найдены частные коэффициенты корреляции (таблица 14).
Таблица 14 – Частные коэффициенты корреляции
| Частные коэффициенты корреляции | Значимость | ||
| r y,x1-x2 | 0,79 | tнабл (r y,x1-x2) | 5,41 |
| r y,x2-x1 | 0,995 | tнабл (r y,x2-x1) | 43,06 |
Поскольку 0,78 < 0,995, то из двух факторов большее влияние оказывает фактор x 2.
Оба частных коэффициента корреляции значимы: |tнабл (r y,x1-x2)| =
= 5,4 > tкр = 2,1, |tнабл (r y,x2-x1)| = 43,06 > tкр = 2,1.
Общий выводпо результатам этапа верификации: так как выполняются все условия верификации, то модель является качественной. Таким образом, прогноз, выполненный по ней, является качественным, т. е. несмещенным, состоятельным и эффективным.
Прогнозирование
Если выполняются все условия верификации, то модель является качественной. В противном случае ее надо усовершенствовать либо на этапе спецификации, либо варьировать выборку. По качественной модели можно прогнозировать значение зависимой переменной при заданных значениях независимых переменных. Точечный прогноз получается подстановкой заданных значений независимых переменных в уравнение регрессии. Интервальный прогноз – это интервал значений зависимой переменной, содержащий с вероятностью 0,95 истинное ее значение при заданных значениях независимых переменных. Центр интервала равен точечному прогнозу, концы интервалов получены прибавлением и вычитанием произведения стандартной ошибки прогноза на критическое значение t -статистики, т. е.  Средняя стандартная ошибка прогноза S *в матричной форме определяется по формуле Средняя стандартная ошибка прогноза S *в матричной форме определяется по формуле
 где S – стандартная ошибка регрессии;
где S – стандартная ошибка регрессии;
 – матрица заданных для построения прогноза значений независимых переменных x 1 = p 1, x 2 = p 2; – матрица заданных для построения прогноза значений независимых переменных x 1 = p 1, x 2 = p 2;
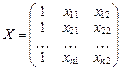 – матрица, составленная из столбца n единиц, столбца n значений переменной x 1 и столбца n значений переменной x 2 из исходных данных;
Т – индекс, обозначающий операцию транспонирования матрицы. – матрица, составленная из столбца n единиц, столбца n значений переменной x 1 и столбца n значений переменной x 2 из исходных данных;
Т – индекс, обозначающий операцию транспонирования матрицы.
|
Поскольку выполняются все условия верификации, то модель является качественной. Следовательно, прогноз, выполненный по ней, является качественным: несмещенным, состоятельным и эффективным. На листе «Регрессия»рассчитан точечный прогноз фактора у, который равен 699,53. На листе «Интервальный прогноз» получен интервальный прогноз (697,38; 701,68), который означает, что с вероятностью 0,95 любое значение из этого интервала является оценкой фактора y.
Вопросы для самоконтроля
1. Каковы этапы построения эконометрической модели?
2. Какова краткая характеристика цели каждого этапа?
3. Знания из каких научных дисциплин необходимы на каждом из этапов эконометрического моделирования?
4. В чем заключается спецификация модели множественной регрессии?
5. Почему в уравнении регрессии присутствует случайная переменная?
6. Как определить силу и направленность взаимодействия факторов?
7. Что означает значимость коэффициента корреляции?
8. Как проверить на значимость коэффициент корреляции?
9. В чем заключается суть МНК для нахождения оценок параметров регрессии?
10. Почему с помощью МНК находятся оценки параметров, а не их точные значения?
11. Какая оценка параметра называется точечной?
12. В чем заключается суть интервальной оценки параметров?
13. Как найти интервальные оценки коэффициентов регрессии?
14. Как используются стандартные ошибки регрессии и стандартные ошибки коэффициентов регрессии при анализе оценок параметров регрессии?
15. В чем заключается экономический смысл параметров модели регрессии?
16. Как можно оценить общее качество уравнения регрессии?
17. Какова суть коэффициента детерминации, нормированного коэффициента детерминации? В каких пределах они изменяются?
18. Какова связь между коэффициентом детерминации, коэффициентом корреляции и множественным коэффициентом корреляции для множественной регрессии?
19. Для какой цели в парной регрессии используется критерий Фишера?
20. Как получить остатки для модели парной регрессии?
21. Какому условию должны удовлетворять остатки, чтобы для проверки статистических гипотез можно было использовать критерий Стьюдента?
22. Какое распределение называется нормальным? Каковы его параметры?
23. Какими способами можно проверить нормальность распределения остатков?
24. Как используется критерий согласия Пирсона для проверки гипотезы о нормальном законе распределения остатков?
25. Для чего и как проверяется значимость коэффициентов регрессии?
26. Какими свойствами должны обладать оценки параметров регрессии?
27. Каковы основные предпосылки применения МНК для построения регрессионной модели?
28. Каковы последствия невыполнимости предпосылок применения МНК?
29. Как сформулировать теорему Гаусса–Маркова?
30. Как проверить центрированность остатков?
31. В чем заключается суть гетероскедастичности (гомоскедастичности) остатков?
32. Каковы причины и последствия гетероскедастичности остатков?
33. Как определить гомоскедастичность остатков?
34. В чем заключается суть автокорреляции остатков? Каковы ее последствия?
35. Как проверить гипотезу об отсутствии автокорреляции остатков с помощью критерия Дарбина–Уотсона?
36. Как проверить гипотезу об отсутствии автокорреляции остатков визуально?
37. Что характеризуют средние коэффициенты эластичности?
38. Для чего используются частные коэффициенты корреляции? Как они рассчитываются?
39. Каковы последствия мультиколлинеарности остатков?
40. Что представляет собой прогнозирование?
41. Как получить точечный прогноз зависимого фактора?
42. Как получить интервальный прогноз зависимого фактора?
Индивидуальное задание
Выполните следующее:
· исследуйте зависимость фактора у от факторов x 1 и x 2, используя данные наблюдений, приведенные в таблице 1, прибавив к значениям фактора y величину 10 × к, где к – номер в журнале;
· постройте регрессионную модель  ;
;
· рассчитайте значение фактора у, если x 1 = 35 и x 2 = 10;
· оформите отчет.
II. НЕЛИНЕЙНАЯ РЕГРЕССИЯ
Постановка задачи
Исследуйте зависимость фактора у от фактора х, используя данные наблюдений, приведенные в таблице 15. Постройте регрессионную модель  Рассчитайте значение показателя у при х = 230.
Рассчитайте значение показателя у при х = 230.
Таблица 15 – Данные наблюдений
| Фактор | Значения | ||||||||||
| x | |||||||||||
| y | 1 310 | 2 697 | 3 137 | 3 641 |
Продолжение таблицы 15
| Фактор | Значения | |||||
| x | ||||||
| y | 5 230 | 9 555 | 12 190 | 21 318 | 44 644 | 86 569 |
|
|
|





 =
=  – коэффициент автокорреляции первого порядка;
– коэффициент автокорреляции первого порядка;

 = 0 и значение статистики d» 2. При положительной автокорреляции
= 0 и значение статистики d» 2. При положительной автокорреляции  а при отрицательной –
а при отрицательной –  Следовательно,
Следовательно, 

 4 –
4 –