 |
Функция плотности распределения системы непрерывных (двух) случайных величин. Определение. Примеры.
|
|
|
|
Функция распределения системы (двух) случайных величин. Определение. Свойства. Примеры.
Функцией распределения системы двух случайных величин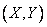 
называется вероятность совместного выполнения двух неравенств 
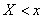и 
:
.
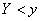Если пользоваться для геометрической интерпретации системы образом случайной точки, то функция распределения 
есть не что иное, как вероятность попадании случайной точки 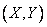в бесконечный квадрант с вершиной в точке 
, лежащий левее и ниже ее (рис. 8.2.1). В аналогичной интерпретации функция распределения одной случайной величины 
- обозначим ее 
- представляет собой вероятность попадания случайной точки в полуплоскость, ограниченную справа абсциссой 
(рис. 8.2.2); функция распределения одной величины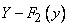 
- вероятность попадания в полуплоскость, ограниченную ординатой у (рис. 8.2.3). 
1. Функция распределения есть неубывающая функция обоих своих аргументов, т. е.
при 
; при 
.
В этом свойстве функции 
можно наглядно убедиться, пользуясь геометрической интерпретацией функции распределения как вероятности попадании в квадрант с вершиной (рис. 8.2.1). Действительно, увеличивая (смещая правую границу квадранта вправо) или увеличивая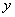 
(смещая верхнюю границу вверх), мы, очевидно, не можем уменьшить вероятность попадания в этот квадрант.
Рис. 8.2.2 Рис. 8.2.3
2. Повсюду на 
функция распределения равна нулю: 
.
В этом свойстве мы наглядно убеждаемся, неограниченно отодвигая влево правую границу квадранта 
или вниз его верхнюю границу 
или делая это одновременно с обеими границами; при этом вероятность попадания в квадрант стремится к нулю.
3. При одном из аргументов, равном 
, функция распределил системы превращается в функцию распределения случайной величины, соответствующей другому аргументу:
|
|
|
, где 
- соответственно функции распределения случайных, функция распределения величин и 
.
В этом свойстве функции распределения можно наглядно убедиться, смещая ту или иную из границ квадранта на ; при этом в пределе квадрант превращается в полуплоскость, вероятность попадания в которую есть функция распределения одной из величин, входящих в систему.
4. Если оба аргумента равны , функция распределения системы равна единице: 
.
Действительно, при 
, 
квадрант с вершиной в пределе обращается во всю плоскость 
, попадание в которую есть достоверное событие.
Пример 2. Двумерная случайная величина 
имеет плотность распределения
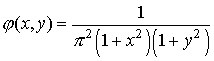
Найти:
1) вероятность р попадания случайной точки 
в квадрат изображенный на рис. 14;
2) функцию распределения F(х,у);
3) плотности распределения каждой величины 
и 
в отдельности. (Решение)
По определению двумерная случайная величина распределена нормально, если плотность распределения системы величин и имеет вид
где 
, 
, а R - некоторая постоянная (см. § 9, п. 2). Можно показать [используя формулы (37) и (38)], что каждая из величин и распределена нормально:
На доказательстве этого факта мы не будем останавливаться. В частности, если и независимы, то 
. Отсюда следует, что R=0, и, cледовательно,
Нетрудно убедиться в том, что справедливо и обратное утверждение: если R=0, то и — независимые случайные величины.
Функция плотности распределения системы непрерывных (двух) случайных величин. Определение. Примеры.
Распределение системы непрерывных величин обычно характеризуют не функцией распределения, а плотностью распределения.
Пусть имеется система двух непрерывных случайных величин 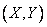, которая интерпретируется случайной точкой на плоскости . Рассмотрим на этой плоскости малый прямоугольник 
со сторонами 
и 
, примыкающий к точке с координатами (рис. 8.3.1). Вероятность попадания в этот прямоугольник по формуле (8.2.2) равна
|
|
|
Рис. 8.3.1
Разделим вероятность попадания в прямоугольник на площадь этого прямоугольника и перейдем к пределу при 
и 
:
(8.3.1)
Предположим, что функция не только непрерывна, но и дифференцируема; тогда правая часть формулы (8.3.1) представляет собой вторую смешанную частную производную функции по и 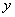. Обозначим эту производную 
:
(8.3.2)
Функция называется плотностью распределения системы.
Таким образом, плотность распределения системы представляет собой предел отношения вероятности попадания в малый прямоугольник к площади этого прямоугольника, когда оба его размера стремятся к нулю; она может быть выражена как вторая смешанная частная производная функции распределения системы по обоим аргументам.
|
|
|
