 |
Центральная предельная теорема
|
|
|
|
Нормальное распределение.
- Нормальное распределение: свойства и график.
- Функция Лапласа.
- Правило трех сигм.
- Примеры решения задач.
Нормальный закон (закон Гаусса) играет исключительную роль в теории вероятностей. Главная особенность закона Гаусса состоит в том, что он является предельным законом, к которому приближаются при определенных условиях. Другие законы распределения. Нормальный закон наиболее часто встречается на практике.
1. Определение. Нормальным называется распределение вероятностей непрерывной случайной величины, которое описывается плотностью вероятности

Нормальный закон распределения также называется законом Гаусса.
Нормальный закон распределения занимает центральное место в теории вероятностей. Это обусловлено тем, что этот закон проявляется во всех случаях, когда случайная величина является результатом действия большого числа различных факторов. К нормальному закону приближаются все остальные законы распределения.
Можно легко показать, что параметры  и
и  , входящие в плотность распределения являются соответственно математическим ожиданием и средним квадратическим отклонением случайной величины Х.
, входящие в плотность распределения являются соответственно математическим ожиданием и средним квадратическим отклонением случайной величины Х.
М(Х) = а
D(X) = s2
s(X) = s
Т.е.
Найдем функцию распределения F(x).

График плотности нормального распределения называется нормальной кривой или кривой Гаусса.
Нормальная кривая обладает следующими свойствами:
1) Функция определена на всей числовой оси.
2) При всех х функция распределения принимает только положительные значения.
3) Ось ОХ является горизонтальной асимптотой графика плотности вероятности, т.к. при неограниченном возрастании по абсолютной величине аргумента х, значение функции стремится к нулю.
4) Найдем экстремум функции.
|
|
|

Т.к. при y’ > 0 при x < m и y’ < 0 при x > m, то в точке х = т функция имеет максимум, равный  .
.
5) Функция является симметричной относительно прямой х = а, т.к. разность
(х – а) входит в функцию плотности распределения в квадрате.
6) Для нахождения точек перегиба графика найдем вторую производную функции плотности.
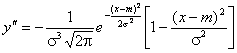
При x = m + s и x = m - s вторая производная равна нулю, а при переходе через эти точки меняет знак, т.е. в этих точках функция имеет перегиб.
В этих точках значение функции равно  .
.
Построим график функции плотности распределения.

Построены графики при т =0 и трех возможных значениях среднего квадратичного отклонения s = 1, s = 2 и s = 7. Как видно, при увеличении значения среднего квадратичного отклонения график становится более пологим, а максимальное значение уменьшается..
Если а > 0, то график сместится в положительном направлении, если а < 0 – в отрицательном.
При а = 0 и s = 1 кривая называется нормированной. Уравнение нормированной кривой:


Функция Лапласа
Найдем вероятность попадания случайной величины, распределенной по нормальному закону, в заданный интервал.

Обозначим 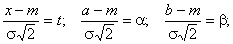
Тогда 
Т.к. интеграл  не выражается через элементарные функции, то вводится в рассмотрение функция
не выражается через элементарные функции, то вводится в рассмотрение функция
 ,
,
которая называется функцией Лапласа или интегралом вероятностей.
Значения этой функции при различных значениях х посчитаны и приводятся в специальных таблицах.
Ниже показан график функции Лапласа.

Функция Лапласа обладает следующими свойствами:
1) Ф(0) = 0;
2) Ф(- х) = - Ф(х);
3) Ф(?) = 1.
Функцию Лапласа также называют функцией ошибок.
Еще используется нормированная функция Лапласа, которая связана с функцией Лапласа соотношением:

Ниже показан график нормированной функции Лапласа.

Используя нормированную функцию Лапласа, вероятность попадания случайной величины в заданный промежуток [a; b] находится по формуле:

3. При рассмотрении нормального закона распределения выделяется важный частный случай, известный как правило трех сигм.
Запишем вероятность того, что отклонение нормально распределенной случайной величины от математического ожидания меньше заданной величины D:

|
|
|
Если принять D = 3s, то получаем с использованием таблиц значений функции Лапласа:

Т.е. вероятность того, что случайная величина отклонится от своего математического ожидание на величину, большую чем утроенное среднее квадратичное отклонение, практически равна нулю.
Это правило называется правилом трех сигм.
На практике считается, что если для какой – либо случайной величины выполняется правило трех сигм, то эта случайная величина имеет нормальное распределение.
Пример 1. Поезд состоит из 100 вагонов. Масса каждого вагона – случайная величина, распределенная по нормальному закону с математическим ожиданием а = 65 т и средним квадратичным отклонением s = 0,9 т. Локомотив может везти состав массой не более 6600 т, в противном случае необходимо прицеплять второй локомотив. Найти вероятность того, что второй локомотив не потребуется.
>Второй локомотив не потребуется, если отклонение массы состава от ожидаемого (100?65 = 6500) не превосходит 6600 – 6500 = 100 т.
Т.к. масса каждого вагона имеет нормальное распределение, то и масса всего состава тоже будет распределена нормально.
Получаем:
 <
<
Пример. Нормально распределенная случайная величина Х задана своими параметрами – а =2 – математическое ожидание и s = 1 – среднее квадратическое отклонение. Требуется написать плотность вероятности и построить ее график, найти вероятность того, Х примет значение из интервала (1; 3), найти вероятность того, что Х отклонится (по модулю) от математического ожидания не более чем на 2.
>Плотность распределения имеет вид:

Построим график:



Найдем вероятность попадания случайной величины в интервал (1; 3).

Найдем вероятность отклонение случайной величины от математического ожидания на величину, не большую чем 2.

Тот же результат может быть получен с использованием нормированной функции Лапласа.
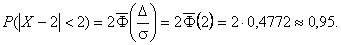
Закон больших чисел
Под законом больших чисел в широком смысле понимается общий принцип, согласно которому, по формулировке академика А.Н. Колмогорова, совокупное действие большого числа случайных факторов приводит (при некоторых весьма общих условиях) к результату, почти не зависящему от случая. Другими словами, при большом числе случайных величин их средний результат перестает быть случайным и может быть предсказан с большой степенью определенности. Под законом больших чисел в узком смысле понимается ряд математических теорем, в каждой из которых для тех или иных условий устанавливается факт приближения средних характеристик большого числа испытаний к некоторым определенным постоянным.
66 Закон больших чисел. Теорема Бернулли. Теорема Пуассона
Схемой Бернулли называется последовательность независимых в совокупности испытаний, в каждом из которых возможны лишь два исхода — «успех» и «неудача», при этом успех в одном испытании происходит с вероятностью 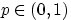 , а неудача — с вероятностью , а неудача — с вероятностью  .
Под независимостью в совокупности испытаний понимается независимость в совокупности любых событий, относящихся к разным испытаниям. В испытаниях схемы Бернулли, когда с одним испытанием можно связать только два взаимоисключающих события, независимость в совокупности испытаний означает, что при любом .
Под независимостью в совокупности испытаний понимается независимость в совокупности любых событий, относящихся к разным испытаниям. В испытаниях схемы Бернулли, когда с одним испытанием можно связать только два взаимоисключающих события, независимость в совокупности испытаний означает, что при любом  независимы в совокупности события независимы в совокупности события 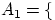 успех в первом испытании успех в первом испытании 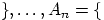 успех в успех в  -ом испытании -ом испытании  . Эти события принадлежат одному и тому же пространству элементарных исходов, полученному декартовым произведением бесконечного числа двухэлементных множеств . Эти события принадлежат одному и тому же пространству элементарных исходов, полученному декартовым произведением бесконечного числа двухэлементных множеств 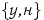 : :
 Здесь буквами «у» и «н» обозначены успешный и неудачный результаты испытаний соответственно.
Обозначим через
Здесь буквами «у» и «н» обозначены успешный и неудачный результаты испытаний соответственно.
Обозначим через  число успехов, случившихся в число успехов, случившихся в  испытаниях схемы Бернулли. Эта величина может принимать целые значения от нуля до испытаниях схемы Бернулли. Эта величина может принимать целые значения от нуля до  в зависимости от результата в зависимости от результата  испытаний. Например, если все испытаний. Например, если все  испытаний завершились неудачей, то величина испытаний завершились неудачей, то величина  равна нулю.
Теорема 10 (формула Бернулли).Для любого равна нулю.
Теорема 10 (формула Бернулли).Для любого  имеет место равенство: имеет место равенство:
 Доказательство.Событие
Доказательство.Событие  означает, что в означает, что в  испытаниях схемы Бернулли произошло ровно испытаниях схемы Бернулли произошло ровно  успехов. Рассмотрим один из благоприятствующих событию успехов. Рассмотрим один из благоприятствующих событию 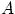 элементарных исходов: элементарных исходов:
 когда первые
когда первые  испытаний завершились успехом, остальные неудачей. Поскольку испытания независимы, вероятность такого элементарного исхода равна испытаний завершились успехом, остальные неудачей. Поскольку испытания независимы, вероятность такого элементарного исхода равна  . Другие благоприятствующие событию . Другие благоприятствующие событию 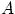 элементарные исходы отличаются лишь расположением элементарные исходы отличаются лишь расположением  успехов на успехов на  местах. Есть ровно местах. Есть ровно  способов расположить способов расположить  успехов на успехов на  местах. Поэтому событие местах. Поэтому событие 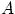 состоит из состоит из  элементарных исходов, вероятность каждого из которых также равна элементарных исходов, вероятность каждого из которых также равна  .
QED
Определение 23.Набор чисел .
QED
Определение 23.Набор чисел  называется биномиальным распределением вероятностей.
Предположим, нам нужна вероятность получить не менее семи успехов в тысяче испытаний схемы Бернулли с вероятностью успеха 0,003. Вероятность этого события равна любому из следующих выражений, вычислить которые довольно сложно: называется биномиальным распределением вероятностей.
Предположим, нам нужна вероятность получить не менее семи успехов в тысяче испытаний схемы Бернулли с вероятностью успеха 0,003. Вероятность этого события равна любому из следующих выражений, вычислить которые довольно сложно:
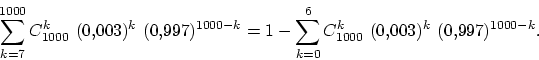 Сформулируем теорему о приближённом вычислении вероятности какого-либо числа успехов в большом числе испытаний схемы Бернулли с маленькой вероятностью успеха. Термин «большое число» должен означать
Сформулируем теорему о приближённом вычислении вероятности какого-либо числа успехов в большом числе испытаний схемы Бернулли с маленькой вероятностью успеха. Термин «большое число» должен означать  . Если при этом . Если при этом 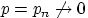 , то, очевидно, вероятность получить любое конечное число успехов при растущем числе испытаний стремится к нулю. Необходимо чтобы вероятность успеха , то, очевидно, вероятность получить любое конечное число успехов при растущем числе испытаний стремится к нулю. Необходимо чтобы вероятность успеха  стремилась к нулю одновременно с ростом числа испытаний. Но от испытания к испытанию вероятность успеха меняться не может (см. определение схемы Бернулли). Поэтому нам придётся рассмотреть так называемую «схему серий»: если испытание одно, то вероятность успеха в нём равна стремилась к нулю одновременно с ростом числа испытаний. Но от испытания к испытанию вероятность успеха меняться не может (см. определение схемы Бернулли). Поэтому нам придётся рассмотреть так называемую «схему серий»: если испытание одно, то вероятность успеха в нём равна  , если испытаний два, то вероятность успеха в каждом — , если испытаний два, то вероятность успеха в каждом —  , и т.д. Если испытаний , и т.д. Если испытаний  , то в каждом из них вероятность успеха равна , то в каждом из них вероятность успеха равна 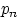 . Вероятность успеха меняется не внутри одной серии испытаний, а от серии к серии, когда меняется общее число испытаний.
Теорема 15 (теорема Пуассона(1)).Пусть . Вероятность успеха меняется не внутри одной серии испытаний, а от серии к серии, когда меняется общее число испытаний.
Теорема 15 (теорема Пуассона(1)).Пусть  и и 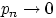 так, что так, что  . Тогда для любого . Тогда для любого  вероятность получить вероятность получить  успехов в успехов в  испытаниях схемы Бернулли с вероятностью успеха испытаниях схемы Бернулли с вероятностью успеха 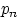 стремится к величине стремится к величине 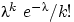 : :
 Доказательство.Положим
Доказательство.Положим  . Тогда . Тогда 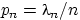 и и
В соотношении (8) мы воспользовались тем, что
QED Определение 25. Набор чисел По теореме 15 можно приближённо посчитать вероятность получить не менее семи успехов в тысяче испытаний схемы Бернулли с вероятностью успеха 0,003, с вычисления которой мы начали. Поскольку
Осталось решить, а достаточно ли Следующую очень полезную теорему мы, исключительно из экономии времени, доказывать не станем.
Теорема 16. (уточнённая теорема Пуассона). Пусть
Таким образом, теорема 16 предоставляет нам возможность самим решать, достаточно ли
Можно утверждать, что искомая вероятность заключена в границах (0,034 - 0,009, 0,034 + 0,009) = (0,025, 0,043). На самом деле можно уточнить оценку в теореме 16. Например, можно доказать, что погрешность даже меньше, чем |
Центральная предельная теорема
Первый вариант этой теоремы был доказан в 1912 г. А.М.Ляпуновым. В настоящее время имеется несколько формулировок этой теоремы, различающихся условиями, которые накладываются на случайные величины. Мы приведём простейший вариант центральной предельной теоремы для одинаково распределённых независимых случайных величин.
Пусть  последовательность одинаково распределённых случайных величин с математическими ожиданиями
последовательность одинаково распределённых случайных величин с математическими ожиданиями  и дисперсиями
и дисперсиями 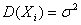 .
.
ТЕОРЕМА. Если случайные величины  независимы и
независимы и  , то при достаточно большом n закон распределения суммы
, то при достаточно большом n закон распределения суммы  будет сколь угодно близок к нормальному закону распределения
будет сколь угодно близок к нормальному закону распределения  .
.
Так как в условиях теоремы случайные величины независимы, то

т.е. в условиях теоремы сумма 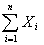 имеет закон распределения близкий к
имеет закон распределения близкий к  .Так' как na и
.Так' как na и 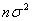 с ростом п, возрастают, то удобнее рассматривать не просто суммы
с ростом п, возрастают, то удобнее рассматривать не просто суммы  , а нормированные суммы
, а нормированные суммы 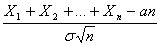 . Такие суммы при
. Такие суммы при  имеют закон распределения
имеют закон распределения 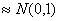 .
.
Мы не приводим доказательства теоремы потому, что оно требует введения многих дополнительных понятий и утверждений. Было потрачено немало усилий, чтобы ослабить условия, налагаемые на случайные величины в центральной предельной теореме. В частности, оказалось, что утверждение теоремы остаётся в силе и для слабо зависимых случайных величин. Как уже отмечалось, существует много вариантов и соответственно формулировок центральной предельной теоремы, но во всех этих вариантах суть условий одна: Если случайная величина может быть представлена в виде суммы большого числа независимых (или слабо зависимых) случайных величин, каждая из которых мала по сравнению с суммой, то эта сумма имеет закон распределения близкий к нормальному.
Пример 1. Наглядной иллюстрацией действия центральной предельной теоремы является рассеивание снарядов при артиллерийской стрельбе. На траекторию снаряда действует большое количество независимых факторов, влияние каждого из которых невелико. Этими факторами являются отклонения в размере заряда, в размере и весе снаряда, сила и направление ветра на разных высотах, плотность воздушных вихрей, зависящая от температуры и влажности воздуха, и т.д.
В результате отклонение снаряда от цели имеет приблизительно нормальный закон распределения.
Пример 2. Другими широко известным примером может служить ошибка возникшая при измерениях. Ошибка, как правило, является суммой малых ошибок возникающих из-за действия случайных факторов таких, как температура окружающей среды, состояние наблюдателя, состояние измерительного прибора и т.д.
Интегральная теорема Лапласа. Пусть X есть число наступлений события в п независимых опытах, в каждом из которых вероятность появления события равна 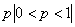 .Тогда при достаточно больших n вероятность того, что событие появится от
.Тогда при достаточно больших n вероятность того, что событие появится от  до
до  раз равна
раз равна
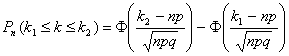 , где q=1-p, Ф(х) – функция Лапласа.
, где q=1-p, Ф(х) – функция Лапласа.
Эта теорема является следствием из, центральной предельной теоремы, хотя и была доказана гораздо раньше неё. В самом деле, число появлений события в n независимых опытах можно представить следующим образом
 число успехов,
число успехов,
где  - число появлений события в i -м опыте, причём ранее было показано, что
- число появлений события в i -м опыте, причём ранее было показано, что  и
и  . Т.е. X является суммой большого числа независимых случайных величин
. Т.е. X является суммой большого числа независимых случайных величин  и
и  . Условия центральной предельной теоремы выполнены, X имеет закон
. Условия центральной предельной теоремы выполнены, X имеет закон
распределения близкий к 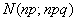
Если для этого закона распределения записать с помощью формулы (**) вероятность попадания случайной величины в интервал  , то и получится утверждение теоремы (Муавра-Лапласа).
, то и получится утверждение теоремы (Муавра-Лапласа).
Пример 1. Вероятность выпуска изделия второго сорта равна 0,2. Изделия отправляют партиями по 100 штук. Какова вероятность того, что во взятой наугад партии содержится от 20 до 25 изделий второго сорта?
Имеем n=100, р=0.2, q=0.8

Законы распределения частоты события.
Рассмотрим частоту появления события в схеме n независимых опытов. Она может быть представлена через индикатор события I  , рассмотренный в дискретных с.в.,
, рассмотренный в дискретных с.в.,  в виде
в виде
 ,
,
т.е. является суммой большого числа независимых одинаково распределенных случайных величин  , каждая из которых имеет дисперсию
, каждая из которых имеет дисперсию  . По центральной предельной теореме частота события имеет закон, близкий к нормальному закону распределения, с параметрами
. По центральной предельной теореме частота события имеет закон, близкий к нормальному закону распределения, с параметрами
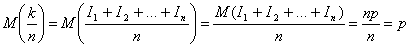
 .
.
Итак, частота события  имеет закон распределения, близкий к нормальному N(p,
имеет закон распределения, близкий к нормальному N(p,  ). Используя формулу (***), можно получить соотношение
). Используя формулу (***), можно получить соотношение
P(  =2
=2 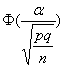 .
.



 и замечательным пределом
и замечательным пределом  . Докажем последнее свойство:
. Докажем последнее свойство:
 называется распределением Пуассона с параметром
называется распределением Пуассона с параметром 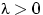 .
. «велико», а
«велико», а 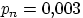 «мало», то, взяв
«мало», то, взяв  , можно записать приближённое равенство
, можно записать приближённое равенство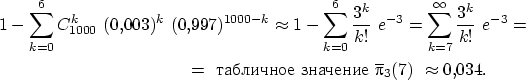
 велико, а
велико, а 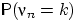 на приближённое значение
на приближённое значение 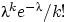 . Для этого нужно уметь оценивать разницу между этими двумя вероятностями.
. Для этого нужно уметь оценивать разницу между этими двумя вероятностями.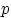 ,
,  . Тогда
. Тогда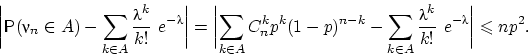
 , имеем:
, имеем:
 . В нашем примере это втрое уменьшает оценку для погрешности —0,003 вместо 0,009, уточняя границы для истинной вероятности: (0,031, 0,037).
. В нашем примере это втрое уменьшает оценку для погрешности —0,003 вместо 0,009, уточняя границы для истинной вероятности: (0,031, 0,037).