Дифференциальное уравнение затухающих колебаний для пружинного маятника.

Гармонические колебания

Простейшими из колебаний являются гармонические колебания, т.е. такие колебания, при которых колеблющаяся величина изменяется со временем по закону синуса или косинуса.

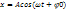Механические колебания, которые происходят под действием силы (восстанавливающая сила), пропорциональной смещению и направленной противоположно ему, называют гармоническими колебаниями -диференциальное уравнение, -решение

x- смещение колеблющейся величины от положительного равновесия

 

66.Основные харак-ки ГК

А – амплитуда- максимальное смещение от положения равновесия

₀ ) – фаза колебаний – определяет смещение в данный момент времени

₀ – начальная фаза – определяется положением системы в начальный момент времени

ω – собственная частота колебаний, определяется параметрами системы

Роль начальных условий – А, начальная фаза

 

67.Способы графического представления колебательных процессов:

-плоская диаграмма

-векторная диаграмма

 

 

68.Векторная диаграмма – способ графического задания колебательного движения в виде вектора.

Возьмем ось, которую обозначим буквой х. Из т. О, взятой на оси, отложим вектор длины а, образующий с осью угол α. Если привести этот вектор во вращение с угловой скоростью ω₀, то проекция конца вектора будет перемещаться по соси х в пределах от –а до +а, причем координата этой проекции будет изменяться со временем по закону х=а cos (ω₀t + α).

Следовательно, проекция вектора на ось будет совершать гармоническое колебание с амплитудой, равной длине вектора, с круговой частотой, равной угловой скорости вращения вектора, и с начальной фазой, равной углу, образуемому вектором с осью в начальный момент времени.

Т.о. гармоническое колебание может быть задано с помощью вектора, длина кот равна амплитуде колебания, а направление вектора образует с осью х угол, равный начальной фазе колебаний.

 

69.Пружинный маятник – груз, подвешенный на пружине.

Выведем диф ур-е пружинного маятника

∑F=ma

 

70.Математическим маятником называют идеализированную систему, состоящую из невесомой и нерастяжимой нити, на которой подвешена масса, сосредоточенная в одной точке. Отклонение маятника от положения равновесия будем характеризовать углом , образованным нитью с вертикалью. При отклонении маятника от положения равновесия возникает вращающий момент М, равный M=-mgl sin .Он имеет такое направление, что стремится вернуть маятник в положение равновесия.

 

71.Физический маятник – любое твердое тело, имеющее ось вращения, которая не совпадает с центром масс.

Вывод дифференциального ур-я колебаний:

 

 

72.Приведенная длина физического маятника – длина такого матем маятника, период колебаний которого совпадает с периодом данного физического маятника.

собственная частота для пружинного маятника

- собственная частота математического маятника

 

73. Периодические или почти периодические изменения заряда, силы тока и напряжения называются электромагнитными колебаниями.

Простейшая система, в которой могут происходить свободные электромагнитные колебания, состоит из конденсатора и катушки, присоединённой к его обкладкам. Такая система называется колебательным контуром.

Частота колебаний – это число колебаний в единицу времени. υ = 1/T

Продолжительность одного полного колебания называется периодом колебания. T = 1/υ

,

где L – индуктивность, С - электроемкость

 

74.Сложение коллинеарных колебаний одинаковой частоты:

Смещение х колеблющегося тела будет суммой смещений х1 и х2, которые запишутся след образом: х₁=а₁ cos (ω₀t+α₁) х₂=а₂ cos (ω₀t+α₂)

Представим оба колебания с помощью векторов а1 и а2. Построим по правилам сложения векторов результирующий вектор а. Проекция этого вектора на ось х равна сумме проекций слагаемых векторов: х1=х1+х2. След-но, вектор а представляет собой результирующее колебание. Этот вектор вращается с той же угловой скоростью ω_0, как и векторы а1 и а2, так что результирующее движение будет гармоническим колебанием с частотой ω_0, амплитудой а и начальной фазой α.

75. Пусть маленькое тело колеблется на взаимно-перпендикулярных пружинках одинаковой жесткости. По какой траектории будет двигаться это тело? Это уравнения траектории в параметрическом виде.

Для получения явной зависимости между координатами x и y надо из уравнений исключить параметр t. Из первого уравнения:

Из второго: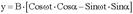

После подстановки:

Избавимся от корня: 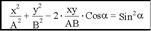- это уравнение эллипса.

 

 

76.В реальных условиях всегда присутствуют рассеянные силы (десепативные?), приводящие к уменьшению энергии в контуре. Рассмотрим частный случай механических колебаний при наличии силы вязкого трения.

-дифференциальное уравнение затухающих колебаний

, - амплитуда затухающих колебаний

 

77.Основные параметры затухающих колебаний.

ω0- собственная частота колебательной системы, без затухания,β - коэффициент затухания- характеризует скорость затухания

- время релаксации, в течение которого амплитуда уменьшается в е раз.

Добротность - показатель скорости ухода энергии из колебательной системы

Q=2π , где Е-энергия, запасенная в контуре, - энергия за период. Q=πNe, гдеNe – кол-во колебаний за время релаксации.

Дифференциальное уравнение затухающих колебаний для пружинного маятника.

79.Дифференциальное уравнение для затухающих колебаний э\м контура

Его решением является функция

q(t)=q₀e^-βtcos(ωt+ ), где частота колебаний ω= Для колебательного контура

80.Амплитуда и частота затухающих колебаний , - амплитуда затухающих колебаний

ω0- собственная частота колебательной системы, без затухания.Частота затухающих колебаний меньше чем собственная частота.

Амплитуда уменьшается по экспоненциальному закону

 

81.Апериоднический и критический режимы:

-периодический или колебательный режимзатухания незначительные, оно мало и этот колебательный процесс можно характеризовать параметрами обычного гармонического колебания без затухания

-критический режим ,

-апериодический режим (непериодический)

утечка энергии происходит так быстро, что система не способна пройти положение равновесия. - не имеет смысла

 

82.

f₀ – амплитуда вынужденной силы - частота вынужденной силы

Решение дифференциального уравнения вынужденных колебаний - ξ(t) - состоит из двух слагаемых: ,где

здесь - - частота затухающих колебаний.

 

τ- переходный режим, после него колебания устанавливаются с частотой вынуждающей силы.

 

83. Вынужденные колебания – совершаются в колебательных системах под действием внешней периодической силы, меняющейся по гармоническому закону:

f₀ – амплитуда вынужденной силы

- частота вынужденной силы

Амплитуда вынужденных колебаний зависит от частоты вынуждающей силы.

Резонанс – явление резкого возрастания амплитуды при частоте вынужденных колебаний близкой к собственной.

-резонансная частота

 

 

84.Амплитудно – частотные характеристики. В контуре с большой добротностью амплитуда резонанса велика, но мала полоса пропускания, а в контуре с резкой добротностью амплитуда мала, но большая ширина полосы пропускания в контурах, где коэф затухания близок к критическому.

Поделиться:

Воспользуйтесь поиском по сайту: