Уравнение касательной плоскости и нормали к поверхности в точке (вывод)

Плоскость α проходит через точку М₀(x₀,y₀,z₀), то ее уравнение может быть записано в виде А(х-х₀)+В(у-у₀)+С(z-z₀)=0, которое можно переписать так: z-z₀=A₁(x-x₀)+B₁(y-y₀) (1)

(разделив уравнение на –С и обозначив А/-C=A₁, В/-C=B₁).

Найдем А₁ и В₁.

Уравнения касательных l₁ и l₂ имеют вид

z-z₀=f′_y(x₀,y₀)∙(y-y₀), x=x₀;

z-z₀=f′_x(x₀,y₀)∙(x-x₀), y=y₀;

соответственно.

Касательная l ₁ лежит в плоскости α, следовательно, координаты всех точек l ₁ удовлетворяют уравнению (1). Этот факт можно записать в виде системы

z-z₀=f′_y(x₀,y₀)∙(y-y₀)

x=x₀

z-z₀=A₁(x-x₀)+B₁(y-y₀)

Разрешая эту систему относительно В₁, получим, что В₁=f′_y((x₀,y₀).

Подставив значения А₁ и В₁ в уравнение (1), получаем уравнение касательной плоскости:

z-z₀= f′_x(x₀,y₀)∙ (х-х₀)+ f′_y(x₀,y₀)∙(y-y₀)

Прямая, проходящая через точку М₀ и перпендикулярная касательной плоскости, построенной в этой точке поверхности, называется ее нормалью.

Используя условие перпендикулярности прямой и плоскости, легко получить канонические уравнения нормали:

Теорема о дифференцировании сложной функции (1-я теорема – доказать, 2-я – без док.)

Теорема1:

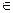Пусть задана z=f(x,y) определена на D и , t (α,β)

Для любого t₀ 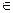(α,β) должен соответствовать | x(t₀),y (t₀ ) 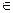D.

Пусть выполняются два следующие условия:

1) функция z=f(x,y) имеет частные непрерывные производные в D дz/дx; дz/дy

2) функции x=x(t), y=y(t) имеют непрерывные производные dx/dt; dy/dt на множестве (α,β), тогда существует производая сложной функции dz/dt и находятся по следующей формуле

Док-во:

Рассмотрим функцию z=f(x,y)=f(x(t),y(t))

из 1) z - дифференцируема. По определению

(*) ; ; ;

Выберем Δx и Δy специальным образом зависящие от Δt:

Δx=x(t₀+ Δt)-x(t₀);Δy= y(t₀+ Δt)-y(t₀)

в силу непрерывности функции x(t) и y(t)

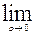
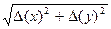=0 поделив (*) на Δt≠0 получим

; z′_t=z′_xx′_t+ z′_yy′_t

Теорема2(более общий случай)

Пусть z=f(x,y), определена в области D. определена областью G причем выполняется, если (U,V) 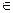G,то x(U,t),y(U,t) 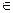D

Пусть выполняются условия:

1) для z=f(x,y) существуют непрерывные частные производные

2) для существуют частные производные, тогда существуют производные сложной функции

Если функция будет иметь больше переменных, то увеличится число слагаемых.

27. Теорема об и нвариантности формы первого дифференциала (доказать для случая z=U(x,y)).

Пусть z=f(x,y), где , удовлетворяет условию теоремы (Пусть задана z=f(x,y) определена на D и , t 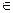(α,β))

Для любого t₀ 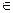(α,β) должен соответствовать | x(t₀),y (t₀ ) 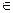D.

Пусть выполняются два следующие условия:

1) функция z=f(x,y) имеет частные непрерывные производные в D дz/дx; дz/дy

2) функции x=x(t), y=y(t) имеют непрерывные производные dx/dt; dy/dt на множестве (α,β), тогда существуют производные сложной функции dz/dt и находятся по следующей формуле dz/dt= дt/дx∙ dx/dt+ дz/дy∙ dy/dt)

тогда

Форма 1-го дифференциала функции 2-х (и более) переменных не зависит от того являются ли х и у независимыми переменными или являются функциями других независимых переменных.

Док-во:

 

 

Понятие производной по направлению (вывод)

Рассмотрим в области D функцию U=U(x,y,z) и (.) M(x,y,z). Проведем из М вектор S, направляющие косинусы которого cosa, cosb, cosg, где a,b,g-соотв-ие углы. На векторе S на расстоянии ∆S от его начала рассмотрим (.) М1(x+∆x, y+∆y, z+∆z). Таким образом ∆s= . Будем предполагать, что функция U(x,y,z) непрерывна имеет непрерывные производные по своим аргументам в области D. Полное приращение функции представим в виде: ∆U= (1), где Е1, Е2,Е3 – стремятся к 0, при ∆s→0. Разделим все части равенства (1) на ∆s: ∆U/∆s= (2). Очевидно, что , , . Следовательно, равенство (2) можно переписать так: = (3).

Предел отношения при ∆s→0 называют производной от функции U=u(x,y,z) в точке (x,y,z) по направлению вектора S и обозначается т.е: = таким образом, переходя к пределу в равенстве (3) получим:

= (5). Из формулы (5) следует, что зная частные производные, легко найти производную по любому направлению S.

Замечание: Сами частные производные являются частным случаем производной по направлению.

 

⇐ Предыдущая1234567Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: